不同波速对刚构桥地震响应影响分析

文小和，陈丽军

（武汉市政工程设计研究院有限责任公司，湖北武汉430023）

1 概述

近年来，高墩大跨刚构桥得到了迅猛的发展，跨度屡创新高，与其他桥型类似，抗震也是大跨刚构桥无法回避的问题，地震输入问题是进行结构地震反应分析的前提和基础。到目前为止，桥梁结构地震反应分析方法主要分为两大类：一类是以地面运动为确定过程的确定性地震反应分析，一类是以地震地面运动为随机过程的概率性地震反应分析。而实际上在地震发生时，许多预应力混凝土刚构桥的跨径都在百米以上，而典型的地震波波长为百余米至数百米，此时就需要考虑不同地面支撑点之间的运动相位差，即行波效应问题。本文基于以上理论基础，运用有限元计算软件MIDAS/CIVIL实现了考虑不同视波速的行波效应作用下广元嘉陵江特大刚构桥的地震反应分析，并与一致激励下的结果进行了对比，指出对于大跨度刚构桥非一致激励分析的必要性，其结果将为大跨刚构桥的地震设计提供一定的参考。

2 行波效应下结构的运动方程

分块形式表达的结构的运动方程为：

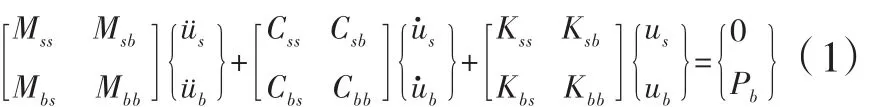
由式（1）的前一组方程可以得到：

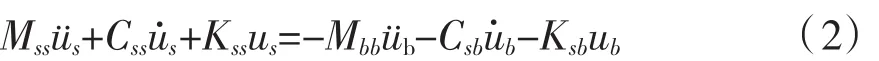
各节点的位移可分为相对动力项d和拟静力项 S，即：

称为拟静力模态矩阵，其力学意义为由结构支座节点的单位静位移所引起的结构非支座节点的拟静力位移。

将式（4）代入式（2）并利用式（5）可以得到结构动力反应的控制方程：

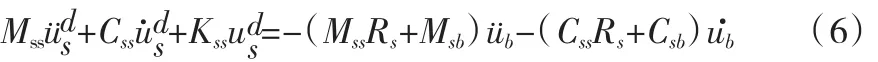
对于通常的工程结构，阻尼对上式右端项的贡献很小，可以略去。这样就得到了求解比的二阶动力学方程：

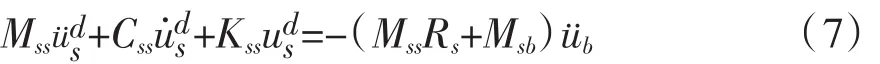
3 有限元模型及其动力特征

3.1 工程概况及计算模型

广元嘉陵江特大桥主桥为105 m+200 m+105 m预应力混凝土连续刚构桥。上部结构为单箱单室变截面箱梁，支点处梁高12.75 m，跨中和边跨端部梁高4.1 m，梁高从根部12.75 m按照1.6次方抛物线变化到跨中4.1 m，底板厚度由根部1.6 m按照1.5次方抛物线变化到跨中底板0.36 m，顶板厚度为30 cm。

大型空间有限元软件MIDAS/Civil在考虑地震的行波效应时，通过给予不同的桥墩以不同的地震波或者给予到达时间的延迟（或者相位差）来考虑，而多点激励分析就是给不同支座输入不同的地面运动的分析方法，MIDAS/Civil的多点激励分析采用的是相对位移法。

本文采用大型空间有限元软件,MIDAS/Civil建立了全桥三维空间有限元模型，顺桥向为x轴、横桥向为y轴、竖向为z轴。变截面箱梁。桥墩。承台均采用梁单元模拟。全桥共划分为个253节点和248个单元，模型见图1。

图1 全桥计算模型

3.2 全桥动力特性分析

结构的动力特性取决于结构的组成体系、刚度、质量分布和支撑条件，主要包括固有频率、振型、阻尼等。桥梁结构的抗震性能是建立在桥梁结构动力特性的基础上的，根据《JTG_T_B02-01-2008公路桥梁抗震设计细则》要求，振型在各个方向的参与质量必须达到90%以上，对前述模型进行了Ritz法进行特征值分析，计算了前90阶模态，X、Y、Z方向的振型参与质量分别达到 99.94%、99.97%、99.9%，满足抗震设计要求。全桥动力特征的部分计算结果见表1及图2。

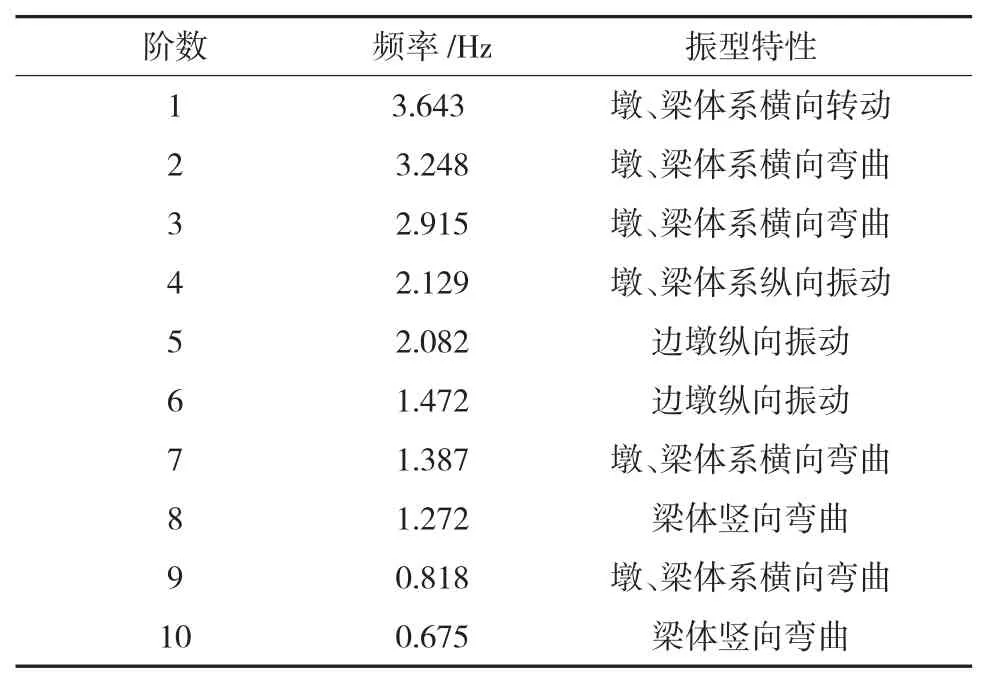
表1 全桥动力特性

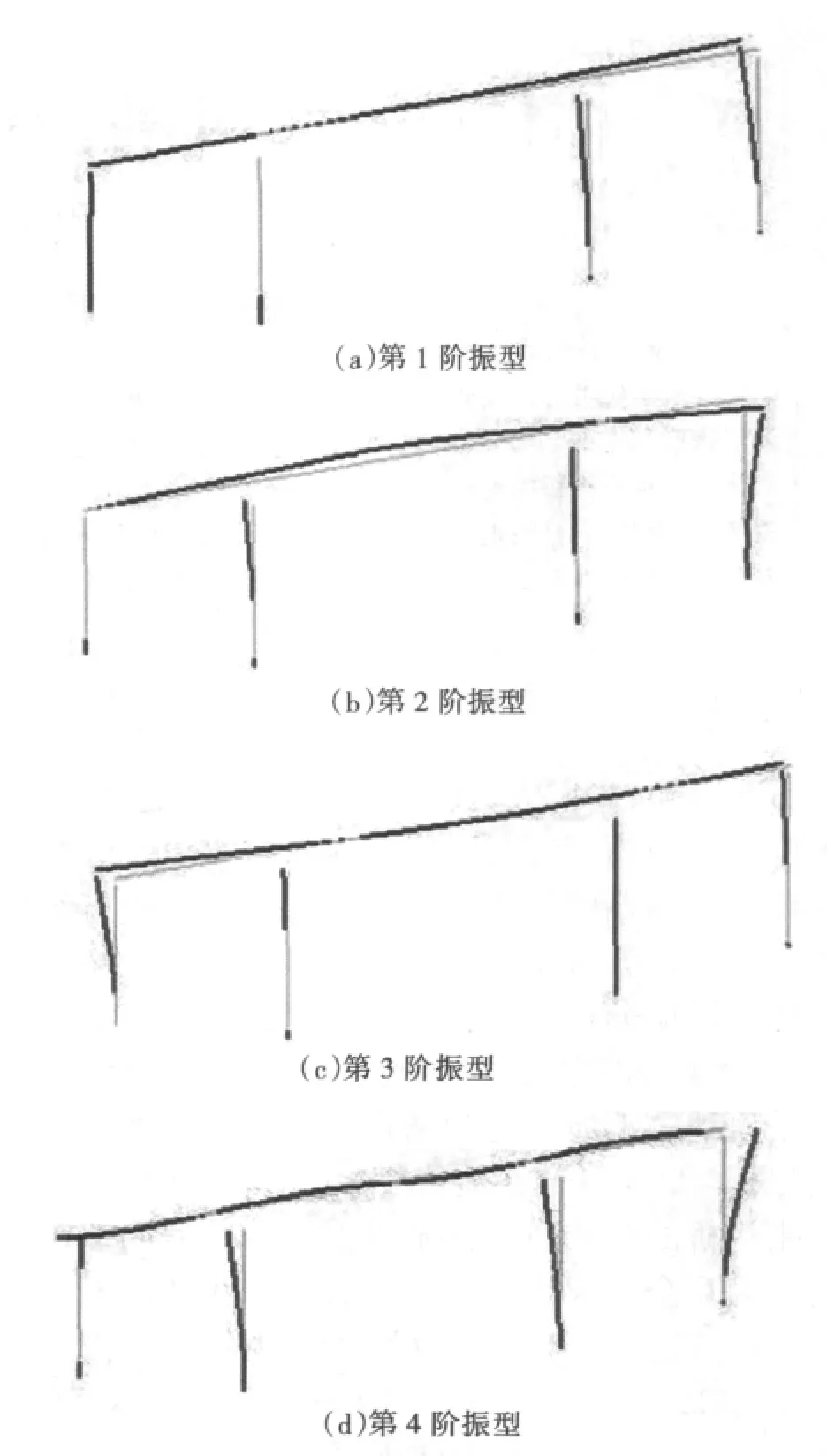
图2 前4阶振型

4 考虑行波效应的桥梁动力时程分析

到目前为止，基岩上的强震加速度记录还很少，且强震地震波一般要经过土层才能传播到结构，需要进行土层分析后才可作为输入到结构的地震波。为方便分析，采用天然强震加速度记录，通过采用一些天然强震加速度记录的比较，采用结构地震分析中常用的El–Centro地震波。取El–Centro地震波水平方向的加速度峰值为0.1 g，计算中取时长0.02 s,共1 000步，计算总时长20.00 s，加速度时程见图3。

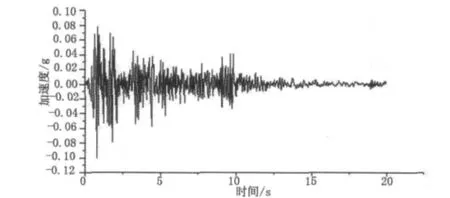
图3 E l–Centro波加速度时程

地震输入采用一致激励和非一致激励，其中非一致激励采用行波激励，2种激励都采用大质量法实现。由于只是比较波速的影响，本模型只输入纵向地震波，假定震源出现在1#桥墩左侧，地震波从1#墩向4#墩传播，考虑到地震波在基岩中的传播速度一般大于500 m/s，分别取波速为600、800、1 000、1 200、1 400 m/s五种情况，依次从 1#、2#、3#、4#墩承台底输入地震波，各种波速下承台地震激励滞后时间见表2。

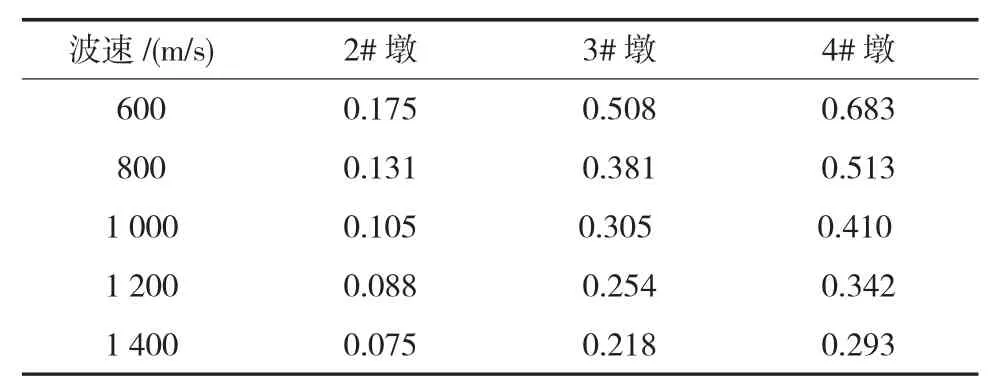
表2 视波波速及各墩墩底激励滞后时间（单位：s）

地震反应分析中的矩阵采用Rayleigh阻尼矩阵，即[C]=α[M]+β[M],其中：

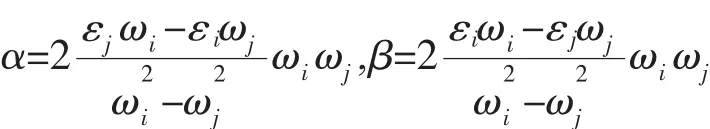
提取前2阶振型的自振频率，根据桥规取阻尼比为 0.05，算得 α=0.172,β=0.015。将计算结果（内力和变形）和未考虑行波效应的一致地震输入情况进行对比，分别提取了各墩顶、墩底和主跨跨中位置的计算结果作为重点考察量值，计算结果见表3。

从以上的行波效应作用下结构的内力反应和一致激励下的内力反应的对比中可以发现存在着明显的滞后现象，在结果中我们可以看出，在波速比较缓慢时候，滞后现象很明显，随着波速的加快，这种滞后现象发生好转，考虑行波效应时，纵向位移会有增大的趋势，这是不同支座处输入的地震波存在相位差而造成的结构内部节点地震响应的平均效应，由计算结果可知，随着视波速的逐渐增大，结构的位移响应也逐渐趋于平缓并逐步逼近一致激励时的位移响应。这说明，行波效应对该刚构桥桥墩是有利的，对主梁则会产生不利影响，所以，一致地震激励输入模式可以控制该桥桥墩的抗震设计，但不能控制该桥的主梁的抗震设计。

5 结论

（1）以上结果的对比表明，考虑非一致激励的行波效应对该桥的桥墩是有利的，对主梁则会产生不利影响，因此在结构设计中，可以用一致地震激励输入模式考虑桥墩的抗震设计，而主梁的抗震设计，必须考虑非一致激励的行波效应。

（2）从以上模型的计算数据可以看出，不同波速作用下的行波效应对高墩大跨连续刚构桥的内力变化影响是不同的，波速越小，滞后效应越明显，随着波速的增大，内力与一致激励时趋近。

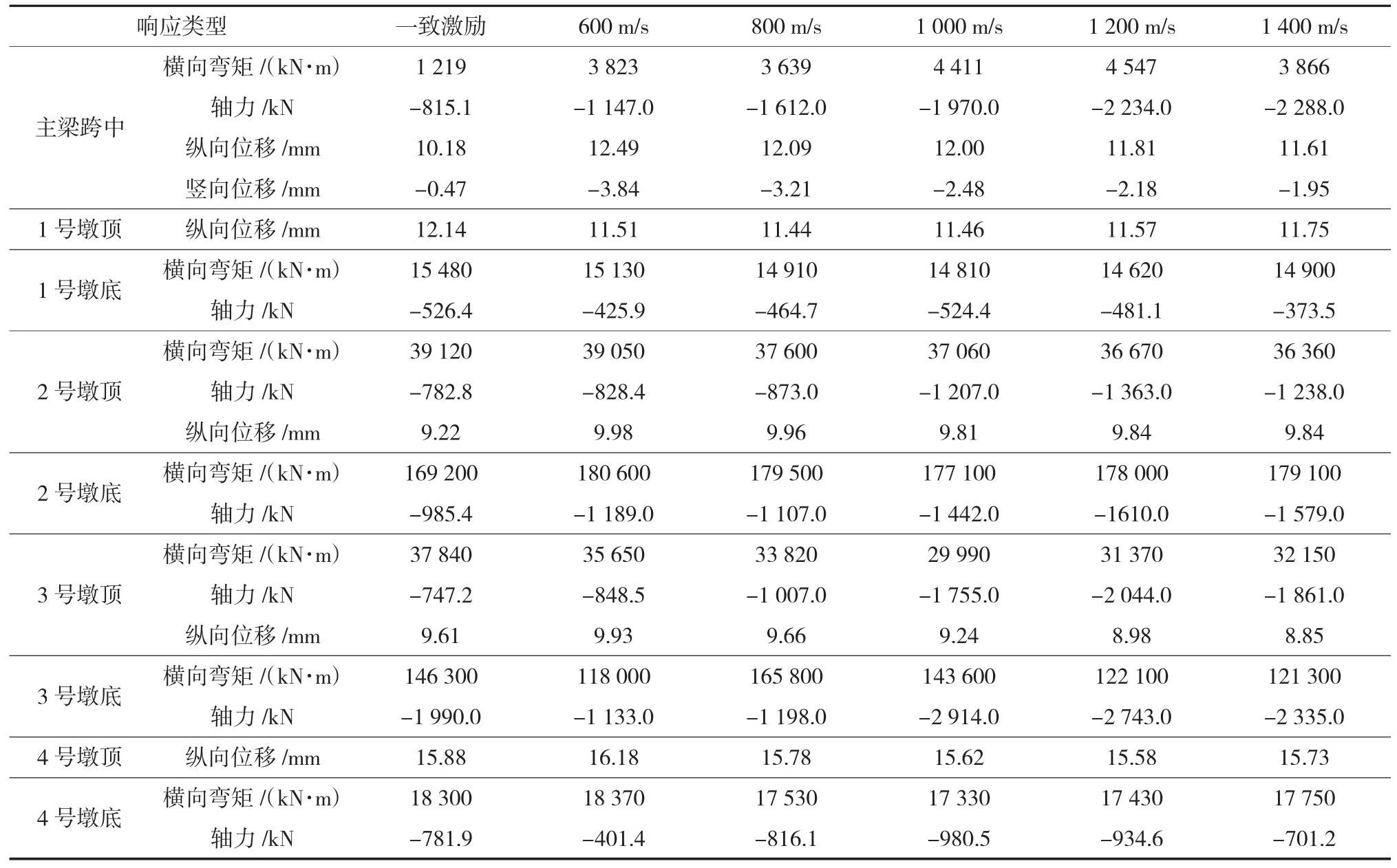
表3 地震荷载作用下桥梁内力及位移响应（单位：s）

（3）行波效应对大跨刚构桥的影响较大，在实际工程实际中，应按照桥梁结构的场地类别，对不同波速下的行波效应进行计算分析，并与一致激励下的作用相比较，按照最不利的情况进行抗震设计验算。

（4）考虑行波效应计算大跨度刚构桥地震响应虽然较一致地震输入有所进步，但是仍然无法真正考虑地震波的入射角度以及地震波的相干性，因而其分析结果仍有一定的局限性，需要全面考虑地震动空间变化的影响。

[1]范立础.桥梁抗震[M].上海:同济大学出版社,1997.

[2]克拉夫·J.结构动力学[M].北京:高等教育出版社,2006.

[3]丰硕,项贻强,王智峰.大跨径连续刚构桥的动力性能及地震响应分析[J].中南公路工程,2005,30(4).

[4]王蕾,赵成刚,汪劲丰.考虑地形影响和多点激励的大跨高墩桥地震响应分析[J].土木工程学报,2006,39(1).

[5]吴东.多点激励下大跨桥梁的地震反应分析[D].成都:西南交通大学,2006.

[6]谢开仲,秦荣,王建军.大跨度钢管混凝土拱桥地震反应分析[J].中南公路工程,2005,30(2).

[7]刘洪冰,范立础.大跨桥梁考虑地形及多点激励的地震响应分析[J].同济大学学报:自然科学版,2003,31(6).

[8]李忠献,史志利.行波激励下大跨度连续刚构桥的地震响应分析[J].地震工程与工程振动,2003,23(2).

[9]Fajfar P.A Nolinear Analysis Method for Performance based Seismic Design[J].Earthquake Spectra,2000,16(8).

[10]张亚辉，李丽媛，陈艳，等.大跨度结构地震行波效应研究[J].大连理工大学学报，2005(4).

[11]J.M.Caicedo.Comparisionof ModelingTechniquesfor Dynamic Analysis of a Cable-Stayed Bridge[A].Proceedingsof the Engineeringmechanics specialty onferenee[C].Austin,Texas,2000.