客专大跨度连续梁转体施工平衡称重分析
蔡军田
(中铁九局集团第七工程有限公司,辽宁沈阳 110044)
1 工程概况
盘锦至营口客运专线盘锦特大桥跨沟海铁路80 m+128 m+80 m转体连续梁,上部结构为单箱单室现浇预应力混凝土连续梁。箱梁顶宽12 m,底宽7 m,中支点处梁高9.6 m,跨中9 m直线段及边跨21.95 m直线段梁高为5.6 m,梁底下缘按二次抛物线变化。腹板厚64~110 cm,底板厚度为52~120 cm,顶板厚度45~65 cm。桥墩基础为钻孔桩基础:桩基直径为1.5 m;边墩承台为二层结构,一层承台为矩形,尺寸为14.6 m×14.6 m×3 m;加台为矩形,尺寸为11 m×8.4 m×2.5 m。中墩承台为三层结构,一层承台为八边形,高5 m,各边尺寸依次为 9.1 m、9.5 m、9.1 m、8.7 m、9.1 m、9.5 m、9.1 m、8.7 m;二层承台为六边形,高3.7 m,各尺寸依次为 7.7 m、7.4 m、7.4 m、7.7 m、7.4 m、7.4 m;三层承台为中间高边缘底的六边形,中间高1.3 m,边缘高0.8 m,各边尺寸依次为9.24 m、4.4 m、4.4 m、9.24 m、4.4 m、4.4 m。盘锦128 m连续梁(主墩号125#、126#)采用平转法转体施工,转体段梁长126 m,梁平面位于半径5 500 m的圆曲线上;,转体角度125#墩为 12°23'、126#墩为 11°28';转体重量12 000 t;球铰转动面为下球缺(凹面)与上球缺(凸面)凸凹面对接形成,其中,球铰球径8 m,球缺弧角27.48°,下球铰凹面镶嵌四氟乙烯片,上下球铰间填充黄油四氟粉。
2 平衡称重目的
为保证桥梁整体拆架过程中转动体平衡安全,转体过程的顺利进行。必须在转体之前进行不平衡分析以及不平衡力矩称重试验,测试转动体的摩阻力矩、静摩擦系数、不平衡力矩和偏心距,进行桥梁转体配重,实现桥梁安全平衡顺利转体合拢。桥梁转动体系必须具备转动性强和平稳性高。对于转动梁体而言,由于球铰体系的制作安装误差、梁体质量分布差异(锯齿块不完全对称,平、竖曲线的影响)、预应力张拉程度等均会导致桥墩两侧悬臂梁段刚度不同、质量分布不同,从而产生不平衡力矩。转体施工的关键构件就是承载整个转动体重量的转动球铰,而转动球铰摩擦系数的大小直接影响着转体时所需牵引力矩的大小。
对于转体施工,转动体系需要易于转动和转动平稳两个基本条件。转体结构的整个重量是由转动球铰来支撑,因此球铰的转动面摩擦系数就直接影响转动牵引力;另外,球铰转动面为上下球缺凸凹面对接形成,那么下球缺(凹面)对上球缺(凸面)的支撑力所提供的自平衡对整个转体过程中的安全平稳起着至关重要作用。实际施工中,由于混凝土超方量、施工临时荷载、风荷载、环境温度的不确定性及安装误差等,转动时达不到理想状态,球铰受力会产生一定的偏心;转动面涂抹黄油四氟粉由于其蠕动性影响,摩擦系数在不同重量下不同。那么转体前,通过称重试验和理论计算,来量化该部分(摩擦系数与偏心等)参数,为转体过程中设备的选择、技术处理措施和安全性能评估提供依据就尤为重要。
3 平衡称重分析方法
3.1 球铰转动法
球铰转动测试不平衡力矩是通过测试刚体位移突变的方法进行的。该法受力明确,而且只考虑刚体作用,不涉及挠度等影响因素较多的参数,结果比较准确。
3.2 基本原理
当脱架完成后,整个梁体的平衡表现为两种形式之一。
(1)转动体球铰摩阻力矩(MZ)小于转动体不平衡力矩(MG)。此时,梁体发生绕球铰的刚体转动,直到撑脚参与工作,体系的平衡由球铰摩阻力矩、转动体不平衡力矩和撑脚对球心的力矩所保持。转动体球铰摩阻力矩小于转动体不平衡力矩时称重试验示意见图1。
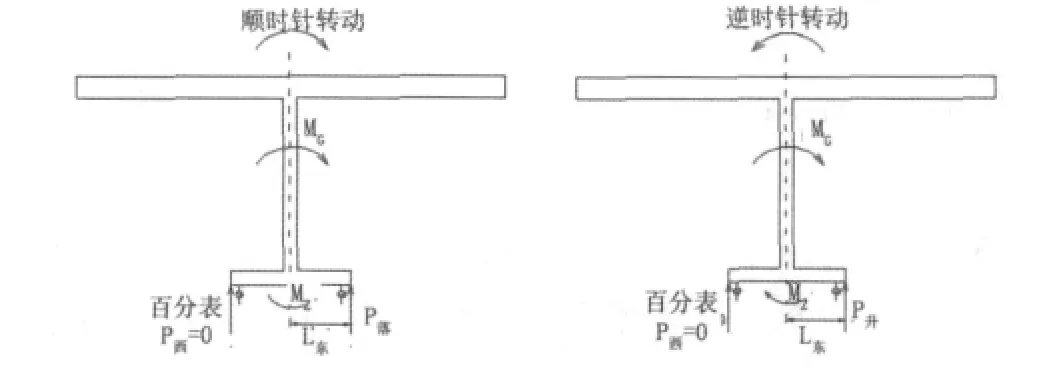
图1 转动体球铰摩阻力矩小于转动体不平衡力矩时称重试验示意图
(2)转动体球铰摩阻力矩(MZ)大于转动体不平衡力矩(MG)。此时,梁体不发生绕球铰的刚体转动,体系的平衡由球铰摩阻力矩和转动体不平衡力矩所保持。转动体球铰摩阻力矩小于转动体不平衡力矩时称重试验示意见图2。

图2 转动体球铰摩阻力矩大于转动体不平衡力矩时称重试验示意图
转动体球铰静摩擦系数的计算:

3.3 测点布置及测点数据
试转前,需进行称重平衡试验,测试转体部分的不平衡力矩、偏心矩、摩阻力矩及摩擦系数等参数,实现桥梁转体的配重要求。在上转盘下用千斤顶施加力,分别用位移计测出球铰由静摩擦状态到动摩擦状态的临界值
根据该状态的测试方法,在两幅梁的承台底面布置的千斤顶和位移传感器见图3,实施两幅梁的不平衡力矩测试。125#墩不平衡称重由于中跨合拢吊架、锯齿块不完全对称等因素影响,预先在小里程梁端配重55 t后进行试验。

图3 称重设备平面及立面布置图
3.4 数据分析及处理
由顶力、位移实测数据绘制顶力-位移曲线见图4~图7。

图4 125#大里程侧顶升时顶力-位移曲线

图5 125#小里程侧顶升时顶力-位移曲线

图6 126#大里程侧顶升时顶力-位移曲线

图7 126#小里程侧顶升时顶力-位移曲线
球铰转动法纵向称重试验数据分析:
从图4、图5可以看出:125#大里程侧顶力临界值P1为5 000 kN,小里程侧顶力临界值P2为5 950 kN;所以,球铰纵向摩阻力矩:MZ=24 090(kN·m),转动体纵向不平衡力:MG=2 090(kN·m),纵向偏心距e=MG/N=1.7×10-2m,纵向滑动时球铰静摩阻系μ=MZ/0.944NR=0.027。
从图6、图7可以看出:126#大里程侧顶力临界值P1为6 000 kN,小里程侧顶力临界值P2为5 880 kN;所以,球铰纵向摩阻力矩:MZ=26 136(kN·m),转动体纵向不平衡力 :MG=264(kN·m),纵向偏心距e=MG/N=2.2×10-3m,纵向滑动时球铰静摩阻系μ=MZ/0.944NR=0.029。
4 结论
(1)球铰转动法能够获得较多的力学参数,如不平衡力矩、摩阻力矩以及摩擦系数等。为转动时牵引力的计算提供了基本参数。其值远小于规范规定值,充分证明了球铰加工的精确度及安装质量的可靠性。
(2)采用球铰转动法对转动体的不平衡力矩进行的理论分析与实验测试,结果表明:球铰转动法所获得的力学参数结果可靠。
(3)利用球铰转动法进行称重实验时,可以在称重实验的同时,进行配重,可快速达到梁体平衡。
(4)通过平衡称重与配重,使撑脚转动时一直处于悬空状态,保证了平衡转体的顺利进行,有效减小了转动中的牵引力。
[1]薛军,任文祥.T形刚构大纵坡弯斜箱梁桥水平转体施工技术[J].铁道标准设计,2005(8):33-37.
[2]翟鹏程.转体梁施工中的不平衡问题及风致振动研究[D].北京:北京交通大学,2008.
[3]李拉普.跨线连续箱梁桥平面转体施工技术[J].铁道标准设计,2009(8):55-57..
[4]周广伟,黄龙华.桥梁转体施工技术[J].华东公路,2007(6):8-10.
[5]陈英杰.桥梁转体施工技术研究与应用[J].中国市政工程,2006(4):28-29.

