一种测量非相干扩频应答机时钟准确度的新方法*

吴有杏，丛 波，梁 盛，段庆光

(中国卫星海上测控部，江苏 江阴214431)

1 引言

非相干扩频技术由于在利用信道容量、无模糊距离以及码分多址等方面具有显著优点[1－2]，已经在航天测控领域逐渐应用起来。它改变了过去单站测单目标的单一模式，可灵活配置以实现多站测单目标和单站测多目标等多种模式。

“北斗”卫星系统采用了高精度铷钟单元[3]，且应用了时钟驯服电路[4]，使得卫星时钟准确度具有了较高的精度。但是某些小型卫星，基于空间及负载的考虑，其载波频率准确度设计要求提得很低且没有校准功能，卫星时钟精度往往比地面设备的相应指标要低4～6个数量级。时钟频率准确度是卫星系统的一个重要指标，对于在轨小卫星系统，可以通过测量星地频差来获取卫星应答机的载波频率准确度。但由于星地频差的测量是基于测速积分公式得到的，其测量值受星地时钟短稳及其他因素影响较大。

本文针对非相干扩频伪码测距的特点，对下行测量帧原始数据和实测距离进行数据分析，对卫星应答机下行测量帧帧周期进行计算，而下行测量帧帧频与载波频率共源，因而可以计算出卫星应答机的时钟准确度。由于该数据分析是通过整个测量周期进行数据统计，从数据变化的趋势来推算卫星时钟频率的准确度，测量精度较高。

2 非相干扩频测距原理[5]

非相干扩频测距，测距通过双向测伪距实现。上、下行信号采用测量帧结构，下行测量帧调制应答机状态信息、星上时间、伪距及伪多普勒测量信息等。图1为非相干扩频测距时序示意图。

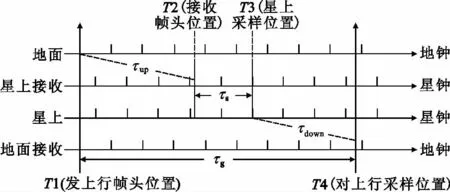
图1 非相干扩频测距示意图Fig.1 The principle of uncoherent spread spectrum ranging

系统完成捕获、稳定跟踪后，T1时刻，地面站测距帧(含帧信息)编帧扩频后发射。卫星接收到上行信号后进行解扩、解调、帧同步，T2时刻为完成帧同步时刻。T3时刻卫星利用自身形成的下行测距信息帧同步(后沿)对接收到的上行信号采样，提取帧内位计数、扩频伪码周期计数、伪码相位、伪码NCO相位等测量信息，将这些采样信息实时放入下行测量帧送至地面。所得到的上述采样值实际上就是利用星上时钟对上行测量帧帧头到达时刻至下行测量帧帧头发出时刻之间的时延量，设为τ's，则星上所形成的伪距值为

地面接收到下行信号后进行解扩、解调、帧同步提取得到下行测量帧同步信号，再利用提取的下行帧同步后沿对自身形成的上行信号进行采样，提取帧计数、帧内位计数、扩频伪码周期计数、伪码相位、伪码NCO相位等测量信息，该时刻为T4。所得到的上述采样值实际上就是利用地面时钟对上行测量帧帧头发出时刻至下行测量帧帧头到达时刻之间的时延量，设为τg，则地面所形成的伪距值为

现有测控体制中，在不考虑卫星和地面时钟不准带来的系统误差的情况下，利用公式(1)、(2)可得到星地实测距离值R:

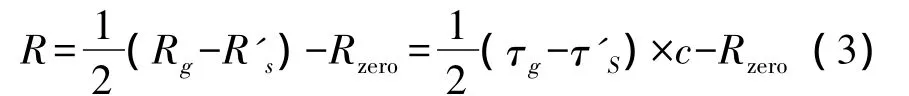
其中，Rzero为卫星和地面设备通过标校得到的设备零值。

3 基于星地帧周期固定差统计的卫星时钟准确度测量方法

图2所示为星地帧周期对应示意图。上行测量帧从Ti时刻发出，卫星收到上行测量帧隔一段时间后，在T'i时刻发出下行测量帧。ΔTi为Ti时刻到T'i时刻之间的时间间隔。

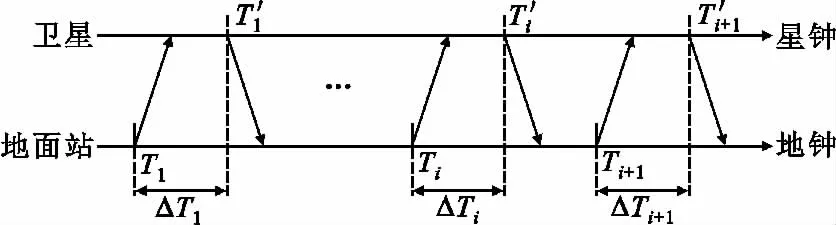
图2 非相干扩频测距星地时序示意图Fig.2 The timing sequence of uncoherent spread spectrum ranging

若在星地均处于静态条件下，且不考虑星地时钟的差异、地球自转和目标运动引起的双向传输时延不对称等因素，则ΔTi为一常量，是星地空间单向传输时延与星上提取的时延量之和。但是在实际工作中，地面站设备时钟采用的是原子钟，其精度往往比卫星时钟精度高4～6个数量级，因此在后面的分析中均以地面站设备时钟为基准，即地面站上行测量帧帧周期为严格的0.5 s，不考虑地面时钟准确度带来的影响。设星上时钟准确度为σs，从图2所示可得

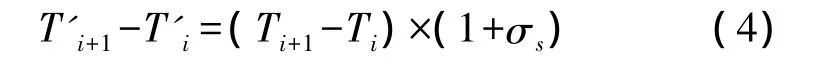
其中，(T'i+1－T'i)为卫星下行测量帧帧周期，设为T';(Ti+1－Ti)为地面站设备上行测量帧帧周期，设为T，则

由式(5)可知，每一帧比前一帧，ΔTi要递增T×σs。从地面接收第1个下行测量帧开始一直到接收到第i+1个下行测量帧:

从图2可以看出，ΔTi由两个时延量组成，一个是上行单向时延(星上设备解调时延为一常量，在计算中不予考虑)，另一个为卫星收到上行测量帧到发出下行测量帧之间的时延量。

当样本量足够大，即测控时间足够长，从数据统计的角度考虑可忽略地球自转和目标运动引起的双向传输时延不对称的因素，对式(6)进行演变，并由此可以推导出卫星时钟频率准确度:

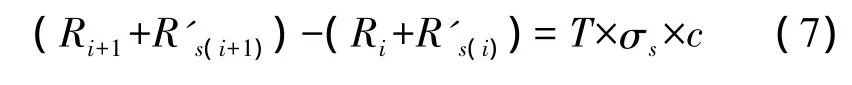
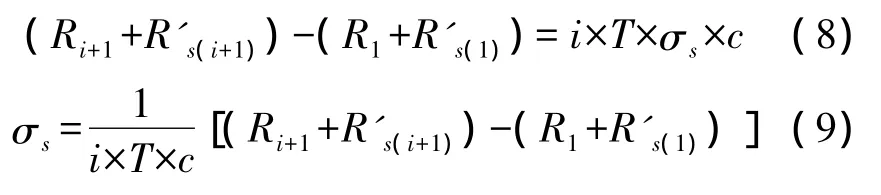
其中，Ri+1为第i+1帧实测距离;R's(i+1)为第i+1帧星上伪距;c为光速;T为地面站上行测量帧帧周期，且 T=0.5 s。

4 实例数据解算验证

为了对基于星地帧周期固定差统计的卫星时钟准确度测量方法进行解算验证，同时对两颗在相同轨道上的小卫星进行了非相干扩频跟踪测距试验。在以下表述中，对两颗小卫星分别命名为卫星1和卫星2。

由于地面站没有下行测量帧数据分析工具，为此编写了下行测量帧数据处理软件和画图工具，便于对星上伪距值进行解析。

4.1 基于下行测量帧解析工具的星上伪距获取方法

地面接收到的下行测量帧中星上伪距信息包括:帧内位计数(BitCntPN')、扩频伪码周期计数(PrdCnt')、伪码相位(PNPhase')、伪码 NCO相位(NcoPhase')等测量信息。为获取直观有效的星上伪距值，第一步需要解决的是对下行测量帧数据进行遥测解调并本地存盘，可通过地面基带设备遥测通道予以完成;第二步，编制下行测量帧解析工具，对下行测量帧存盘原始数据中的二进制代码进行格式分析并转换。图3为下行测量帧解析工具界面示意图。

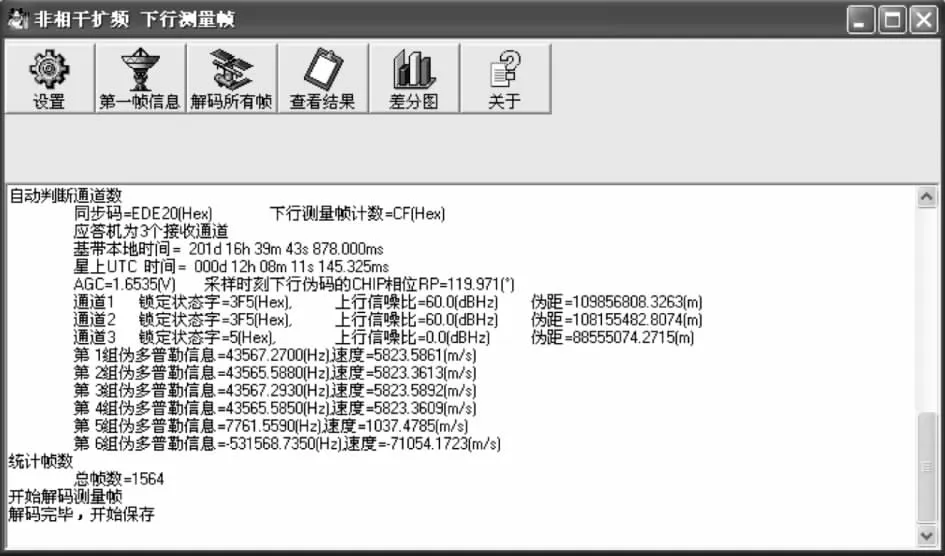
图3 下行测量帧解析工具界面Fig.3 The ranging frame analysis tool

根据非相干扩频测量帧格式及伪距转换公式(10)将每帧的星上伪距予以转换并本地存盘，以供后续的卫星时钟频率准确度解算使用。

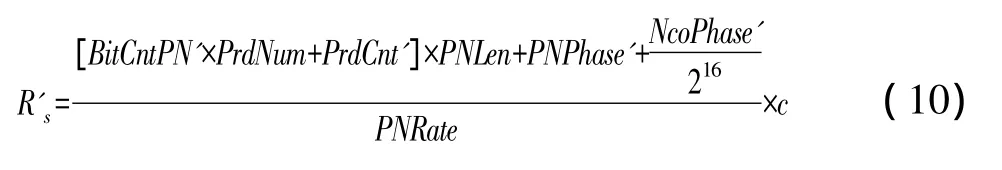
其中，PrdNum为1个数据位内调制的伪码周期数;PNLen为伪码长度;PNRate为伪码速率;c为光速，取值为 2.997 924 58×108m/s。

4.2 卫星时钟频率准确度的解算

图4为卫星1和卫星2星地实测距离示意图，图5为卫星1和卫星2星上伪距数据处理结果示意图，图6为两颗卫星的实测距离与星上伪距求和的示意图。

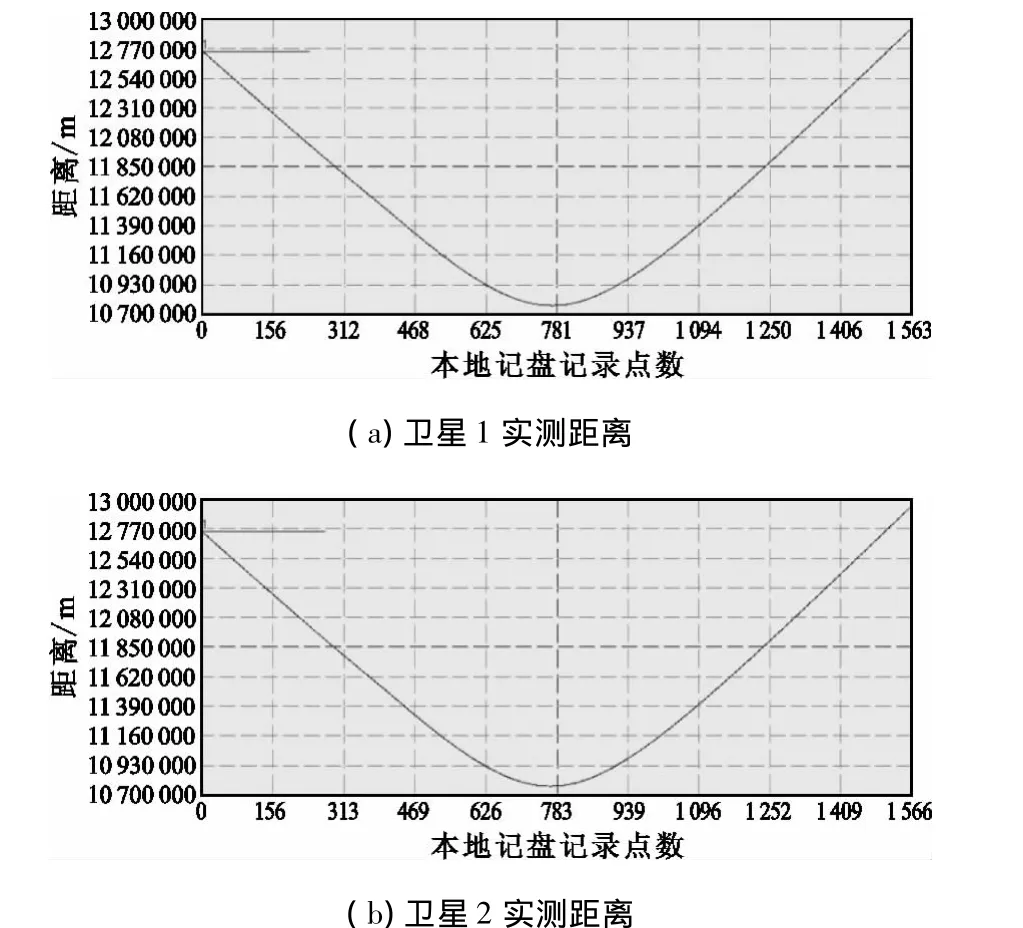
图4 卫星1、卫星2实测距离示意图Fig.4 The real ranging of satellite 1 and 2 from the earth

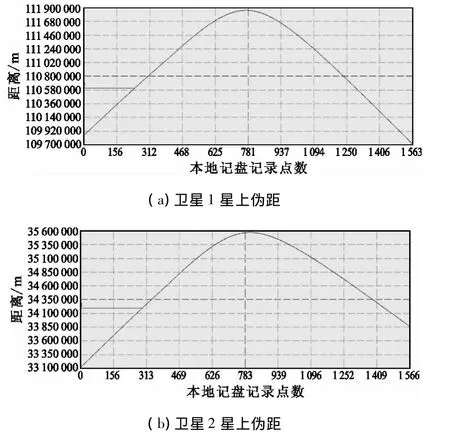
图5 卫星1、卫星2星上伪距示意图Fig.5 The pseudo range of satellite 1 and 2

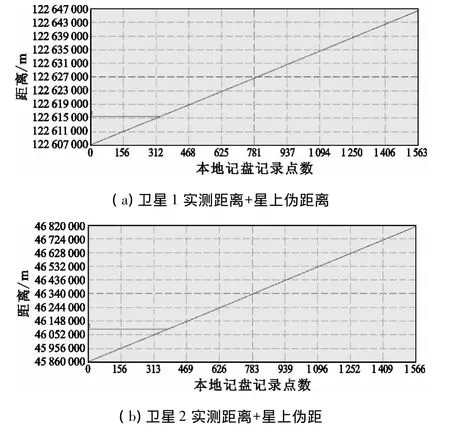
图6 实测距离与星上伪距数据分析Fig.6 The pseudo range and real ranging data analysis

从图6可以看出，两颗卫星实测距离与星上伪距求和之后，随着时间或测量帧的累积，其实测距离与星上伪距之和也在递增，且递增速度衡定不变。这也充分验证了式(7)的正确性。

将图6所示的数据代入式(9)，可得到卫星1和卫星2应答机时钟频率准确度的精确测量值。

在后续不同的时间对这两颗卫星分时、分段进行了测距试验，并进行了同样处理，结果与本次处理结果一致。

5 结束语

采用基于星地帧周期固定差统计的卫星时钟准确度计算分析方法对在轨非相干扩频卫星进行时钟准确度的测量，方法简单易行，精度较高，不同卫星测量结果一致。该方法一方面可以对在轨卫星时钟的健康状态进行监测，另一方面还可以根据计算结果对部分数据进行精确的量化分析，有较高的实用价值。下一步研究方向为非相干扩频测控系统星地测量误差分离技术。

[1]任松，李改芹，陈剑红.伪码扩频航天测控体制设计[J].信息与电子工程，2007，5(3);165－169.REN Song，LI Gai－qin，CHEN Jian－ hong.Design of Pseudo Code Spread Spectrum Aerospace TT＆C System[J].Information and Electronic Engineering，2007，5(3):165－169.(in Chinese)

[2]唐军，谢澍霖，王卫星.航天扩频测控通信系统中伪码测距方法及精度分析[J].电讯技术，2006，46(4):91－95.TANG Jun，XIE Shu－lin，WANG Wei－xing.Pseudo Code Ranging Method and Precision Analysis of Aerospace Spread Spectrum TTC＆DT Systems[J].Telecommunication Engineering，2006，46(4):91－95.(in Chinese)

[3]倪媛媛，胡永辉，何在民.北斗卫星校准铷钟单元的设计与实现[J].数字通信世界，2012(12):60－63.NI Yuan－yuan，HU Yong－hui，HE Zai－min.The Design and Realization of Frequency Calibration for Rb Clock based on BeiDou[J].Digital Communication World，2012(12):60－63.(in Chinese)

[4]单庆晓，杨骏.卫星驯服时钟系统的新进展[J].测试技术学报，2009(5):396－401.SHAN Qing－xiao，YANG Jun.Review of Satellite Disciplined Clock System[J].Journal of Test and Measurement Techol，2009，23(5):396－401.(in Chinese)

[5]吴有杏，房新兵，丛波，等.航天扩频测控系统中非相干伪码测距跳值问题分析及对策[J].电讯技术，2008，48(11):56－60.WU You－xing，FANG Xin－bing，CONG Bo，et al.The Problem of Exceptional Non－coherent PN Ranging Data in Spread Spectrum TT＆C Systems:Analysis and Solution[J].Telecommunication Engineering，2008，48(11):56－60.(in Chinese)