薄壁叶片汽道加工变形模型预测

董久虎 谌永祥 李双跃

(西南科技大学制造科学与工程学院，四川绵阳 621010)

薄壁叶片汽道弧面在加工过程中很容易发生变形，从而产生加工误差。目前主要采用两种方法来提高薄壁叶片的加工精度。一种是通过切削参数优化，减小叶片在加工过程中的变形量;另一种是通过预测叶片加工过程中的变形量，采用误差补偿的方法提高薄壁叶片的加工精度。

国内外很多学者对如何提高薄壁叶片的加工精度进行了研究。Kline和Budak研究了叶片加工过程中刀具的每齿进给量对加工变形的影响，通过减小每齿进给量可以减小切削力，控制叶片变形［1］。武凯等人通过实验分析了薄壁零件的变形规律，提出了薄壁零件的加工变形与零件的尺寸、走刀路径、切削用量等因素的组合有关，并分析了不同加工方法对零件加工精度的影响［2］。Zbignizew Lechnink等通过采用优化刀具轨迹的方法，提高了薄壁叶片的加工精度［3］;Budak E等通过减小进给量来控制薄壁零件的变形，减小加工误差［4］;Yusuf Altintas提出的立铣刀切削力数学模型，完全可以用于预测立铣刀加工零件过程中切削力的大小［5］。文献［6－9］对切削加工力学模型做了大量研究;李阳等人用有限元软件模拟薄壁零件加工时的变形规律［10］;文献［11－12］对在不同的切削条件下对薄壁零件的加工变形进行了有限元数值模拟分析。但是，大多数学者只对形状规则的薄壁零件的切削变形进行了研究分析，很少对复杂弧面加工变形进行模型预测。

本文旨在通过分析不同切削参数对汽轮机叶片汽道内弧变形的影响规律，并运用线性回归的方法，建立了薄壁叶片变形量与主轴转速、进给速度、切削深度、刀具倾角以及叶片汽道表面不同点之间的预测模型。通过模拟研究:薄壁叶片变形量预测模型拟合良好，最大拟合误差为22.855 μm，最小拟合误差为 0.140 μm，平均误差为5.179 μm。

1 薄壁叶片切削力模型建立

由于立铣刀的结构比较复杂，一般求解切削力的大小采用微元的方法，即将切削刃离散成很多微单元，分别对每个单元求解切削力，然后将所有力进行求和。本文采用Yusuf Altintas提出的立铣刀切削力数学模型［5］求解薄壁叶片加工过程中切削力的大小。

式中:hj(ψj(z))为切削深度;ψ 为滞后角;krc、ktc和kac分别表示径向、切向和轴向上的剪切力系数。

由于立铣刀在铣削过程中，刀具端面的切削力远小于刀具圆周上的切削力，对铣削过程的影响很小，在计算立铣刀切削力时，可以忽略刀具端面上的切削力［6］。切削力可表示为

2 薄壁叶片模型简化

薄壁叶片的进汽边和出汽边都比较薄，尤其是出汽边增厚的速度比较缓慢，叶片在精加工过程中更容易发生变形。为了分析薄壁叶片加工过程中的变形情况，对叶片出汽边进行简化，将薄壁叶片出汽边附近的内弧面假设成平面，建立坐标系如下:与叶根相邻的汽道截面的出汽边部分为原点，垂直于该截面指向叶冠的方向为x方向，沿该截面内弧方向为y方向，如图1所示。

当立铣刀加工出汽边附近内弧时，根据Yusuf Altintas提出的立铣刀切削力模型可以求解立铣刀加工薄壁叶片汽道内弧的3个方向的切削力，如图2所示。

3 薄壁叶片变形有限元模拟

3.1 切削力坐标转换

在ABAQUS中模拟薄壁叶片加工变形时，由于立铣刀在加工叶片过程中，存在加工倾角，叶片汽道模型的坐标与立铣刀切削力坐标方向不一致，因此在施加切削力时，需要对其进行转换，如图3所示。由于叶片在精加工过程中，切削深度比较小，切削力比较小，沿薄壁叶片截面方向的切削力对叶片变形影响比较小，可以忽略。因此，有限元模拟叶片变形时，施加在薄壁叶片内弧上两个方向的切削力的大小为:

式中:Fx、Fz为切削力在立铣刀坐标系中x、y方向上的分力;Fx'、Fy'为切削力在工件坐标系中x'、y'方向上的分力;δ为加工倾角;α为简化斜面与工件工件坐标系y'方向夹角。

3.2 薄壁叶片变形有限元模拟

叶片汽道长度为1 000 mm，最小厚度为1.6 mm。叶片材料为硬铝合金［13］(YT15)，弹性模量为700 GPa;泊松比为0.33;剪切模量为2.7×10－5MPa;线膨胀系数为2.36×10－7/K;比热容为871 J/(kg·k);热导率为162 W/(m·K);密度为6.68 g/cm3。薄壁叶片在加工过程中，采用直径为10 mm的三刃立铣刀，切削宽度为 6 mm，刀具前角为15°，刀具螺旋角为 30°。

叶片截面是不规则的光滑曲线，获取叶片加工过程中的变形量采用有限元的方法比较方便。根据立铣刀的切削力数学模型，在不同的切削条件，采用ABAQUS有限元软件，将公式(3)中获取的切削力施加到叶片的结点上，可以预测叶片的变形量，如图4所示(变形量的大小放大了105倍)。叶片模型简化后，左右两侧是对称的，由于切削条件相同，因此只对左侧半部分进行变形分析。在薄壁叶片模型上取5个截面，每个截面上取5个点进行叶片变形有限元模拟。

4 正交实验设计与结果分析

4.1 正交实验设计

为了获取薄壁叶片内弧变形量与不同切削参数之间的关系，设计了正交实验。薄壁叶片变形的主要影响因素有主轴转速n、进给速度f、切削深度ap、刀具倾角δ、X距离(建立的坐标系中，沿X方向距离原点的长度)、Y距离(建立的坐标系中，沿Y方向距离原点的长度)，评价指标是薄壁叶片的最大变形量Δl。其中，因素水平表见表1，正交实验表见表2。

表1 因素水平表

4.2 实验结果分析

根据正交实验表中的数据，可以得出各因素对薄壁叶片变形量影响趋势图，如图5，从图中可以看出:薄壁叶片变形量随着主轴转速的增加而减小，主轴转速越大，刀具每齿的切削厚度会减小，减小了切削力，从而减小了叶片变形量;薄壁叶片变形量随着进给速度的增加而增大，进给速度越大，刀具每齿切削的厚度增加，增加了切削力，叶片变形增大;薄壁叶片变形量随着切削深度、立铣刀加工倾角的增加而增大;立铣刀薄壁叶片变形量随着X增加而增大，因为沿X增加，加工位置逐渐移到叶片中心截面，在相同的切削条件下，薄壁叶片产生的弯矩较大，变形增大;薄壁叶片变形量随着Y的增大而减小，因为沿着Y方向，叶片厚度逐渐增大，在相同的切削力条件下，叶片变形较小。

4.3 线性回归分析

为了预测薄壁叶片出汽边附近汽道表面在不同切削参数条件下的变形量，对叶片变形量Δl进行线性回归分析，主要影响因素为主轴转速n、进给速度f、切削深度ap、刀具倾角δ、叶片表面坐标X和Y。

假设:

式中:K、k1、k2、k3、k4、k5、k6为常数。

两边取对数可得:

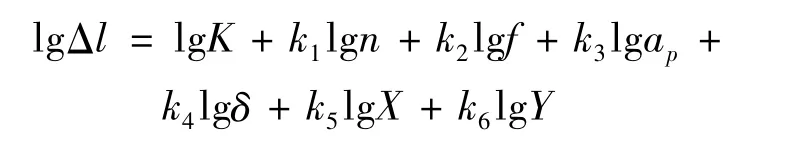
在MATLAB软件中对数据进行处理，可以发现试验号7、8、20、21组数据异常，剔除这几组异常数据，根据多项式线性回归方法，求得叶片变形量Δl的线性回归方程为

将正交实验中25组数据代入到式(5)中，可以求解薄壁叶片的变形量，将其与有限元模拟得到的叶片变形量进行对比，如图6。

从图6中，可以看出:通过线性回归方程求得的薄壁叶片变形量与有限元模拟得到的叶片变形量拟合较好。拟合误差见表3，最大拟合误差为22.855 μm，最小拟合误差为0.140 μm，平均误差为5.179 μm。

表3 线性回归方程拟合误差表

5 结语

通过分析不同切削参数对薄壁叶片变形的影响规律，可以对实际加工薄壁叶片提供一些理论指导，有利于提高薄壁叶片的加工精度。

运用线性回归方法，建立了薄壁叶片变形量与主轴转速、进给速度、切削深度、刀具倾角、X距离和Y距离6个因素之间的预测模型。该模型可以求出在指定加工点，一定的切削条件下薄壁叶片的变形量，为预测叶片在加工过程中的变形量提出了一种可行方法。

在对叶片进行误差补偿时，需要获取薄壁叶片各个点的变形量，通过薄壁叶片变形量预测模型，可以比较容易的获取叶片汽道弧面上各个加工点的变形量，从而大大减小了模拟叶片变形的时间，有利于实现薄壁叶片加工过程中的误差补偿。

［1］Kline W A，Debor R E，Lindberg R.The prediction of cutting forces in end milling with application to cornering cuts［J］.International Journal of Designing Tool＆ Research，1982，22(1):7－2.

［2］武凯，何宁，廖文和，等.薄壁腹板加工变形规律及其变形控制方案的研究［J］.中国机械工程，2004，15(8):670 －674.

［3］Zbigniew Lechniak，Andrzej Wevner，Konstanty Skaiski，et al.Methodology of off－line software compensation for errors in the machining process on the CNC machine tool［J］.Journal of Materials Processing Technology，1998，76(1 －3):42 －48.

［4］Budak E，Altintas Y.Modeling and avoidance of static form errors in peripheral milling of plates［J］.International Journal of Machine Tools and Manufacture，1995，35(3):459 －476.

［5］Yusuf Altintas.数控技术制造自动化［M］.北京:化工工业出版社，2002.

［6］Lee P，Altintas Y.Prediction of ball－end milling forces from orthogonal cutting data［J］.International Journal of Machine Tools and Manufacture，1996，36(9):1059 －1072.

［7］Kim G M，Cho P J.Cutting force prediction of sculptured surface ball end milling usingZ－map［J］.International of Machine Tools＆ Manufacture，2000，40(2):277 －291.

［8］Gradisek J，Kalveram M，Weinert K.Mechanistic identification of specific force coefficients for a general end mill［J］.International of Machine Tools＆ Manufacture，2004，44(4):401－414.

［9］Tsai Chung－lang，Liao Yunn－shiuan.Prediction of cutting force in ball－ end milling by means of geometric analysis［J］.Journal of Materials Processing Technology，2008，205(1 －3):24 －33.

［10］李阳.薄壁零件铣削加工变形预测［D］.大连:大连交通大学，2008.

［11］Ee Meng Lim，Meng C H.Error compensation for sculptured surface productions by the application of control surface strategy using predicted machining errors［J］.Journal of Manufacturing Science and Engineering，1997，119(8):402 －409.

［12］Tsai Jer－Shyong，Liao Chung－Li.Finite－element modeling of static surface errors in the peripheral milling of thin － walled workpieces［J］.Journal of Materials Processing Technology，1999，94(2/3):235 －246.

［13］肖诗纲.刀具材料及其合理选择［M］.北京:机械工业出版社，1990.