铣削过程颤振稳定域建模研究现状与展望*

李忠群 郑 敏

(①湖南工业大学机械工程学院，湖南株洲 412007;②北京航空航天大学机械工程及自动化学院，北京 100191)

通常，铣削是一个由多齿参与的断续切削过程。相对于其它切削加工形式，它具有切削力小、切削温度低、加工变形小、加工能力强、材料去除率高等诸多优点，因而被广泛应用于航空、航天、汽车、模具制造等行业。制约铣削质量与效率的最大因素是切削颤振，它是指切削加工过程中发生的一种自激振动现象，会导致以下3方面的不良后果:首先，直接影响工件的尺寸精度和表面质量、降低切削效率;其次，容易导致机床零件过早出现疲劳破坏、加剧刀具的磨损与破损;第三，会刺激工人引起疲劳，降低劳动生产率。为保证加工质量、提高数控机床的效率，对铣削加工过程进行动力学建模与仿真，对铣削颤振稳定域进行预测，通过切削参数选择与优化实现无颤振切削是国内外众多学者的研究热点。

有关颤振的研究最早可追溯到上世纪中叶，Tobias［1］和 Tlusty［2］开创了颤振研究的先河，发现再生作用是导致颤振发生的主因，进而奠定了再生颤振的理论基础。基于反馈控制理论，Merrit在对再生颤振分析时最早使用了稳定性叶瓣图(Stability Lobe Diagram，SLD)［3］。基于 Floquet理论和 Fourier级数展开，Minis等采用Nyquist判据获得了铣削加工颤振稳定域分析解［4］。Budak提出了求解铣削颤振稳定性叶瓣图的解析方法［5］，该方法得到了切削试验与数值仿真结果的验证［6］，且已应用到球头铣刀铣削稳定性分析中［7］并拓展到三维铣削中［8］。铣削颤振稳定性分析与仿真方法可分为频域法、时域法和切削试验等3大类。

1 频域法

频域法又叫解析求解法，它是指在频域内对切削过程的稳定性进行分析与求解，可细分为零阶频率法(Zero－order Anaytical，ZOA)和多频域法(Multi Frequency，MF)两类。前者最先由Budak提出，采用零阶Fourier级数展开近似求时变方向力系数平均值，从而使问题线性化［5］，是迄今为止仿真速度最快且应用最广泛的铣削稳定性极限预测方法。MF方法由Merdol等提出，在将时变方向力系数进行Fourier级数展开时取多次谐波，实现了对小径向切深铣削(断续切削)稳定性极限图中附加稳定叶瓣的准确预测［9］。与ZOA方法相比，MF方法计算更为复杂。

频域法的一般过程可描述为:

(1)将工艺系统简化为x、y相互垂直方向的二自由度振动系统，并建立用微分方程表示的铣削动力学微分方程(控制方程)。

(2)考虑再生切削效果对动态切削厚度的影响并忽略静态切削厚度，推导出动态切削力时域表达式。

(3)根据Fourier级数展开理论对时变的方向力系数进行近似求解，将时域求解过程转化频域过程。

(4)求解系统的特征方程，根据李雅普诺夫稳定性判据判断其稳定性。

(5)求解临界稳定条件下的轴向切深和主轴转速，绘制出稳定性极限图。

基于经典频域方法，众多学者在该领域展开了诸多拓展，概括起来主要包括:①针对各种复杂刀具几何提出改进的ZOA模型。如Altintas等建立了面向镶齿铣刀的通用几何模型与颤振稳定域模型［10］;笔者通过采用数值方法计算平均方向力系数实现了T型槽铣削颤振稳定域解析预测［11］;Slavicek、Altintas等先后对变齿距铣刀抑制颤振的机理进行了研究，发现改变铣刀的齿间角和螺旋角可以获得更大的极限切深［12－13］，Budak提出了变齿距铣刀的设计模型［14］。②针对各种复杂的加工策略提出改进的ZOA模型。如Kardes等通过考虑时变的浸入角和方向力系数，建立了面向圆弧走刀轨迹的铣削动力学方程并用频域进行了求解［15］。笔者通过对圆弧铣削进行几何与动力学建模得到了将直线铣削颤振稳定域解析模型应用于圆角铣削的条件，解决了非直线铣削颤振稳定域求解及其工程应用问题［16］。③将经典二维铣削颤振模型拓展到三维乃至多维模型。如Bravo等提出了适用于机床和工件同为弱刚性结构的工艺系统颤振稳定域求解方法，并根据薄壁工件加工时刀具与工件的相对运动来获得三维颤振稳定性叶瓣图［17］。Vincent等利用经典颤振模型用解析法构建出三维颤振稳定性叶瓣图，根据工件与刀具相对位置确定优化的切削参数［18］。笔者在构建T型槽铣削颤振稳定域解析模型时，通过改变径向切深仿真获得三维颤振稳定域图形，并因此获得了给定轴向切深下的颤振稳定域图以满足T型槽铣削的切削参数优化，典型三维颤振稳定性叶瓣图如图1所示［19］。④系统地分析加工条件，尤其是工艺系统动力学特性参数对切削稳定性的影响，以便通过切削条件优化来避免颤振的发生［20］。

2 时域法

时域法，是指在时间域内对铣削过程稳定性进行分析、仿真的方法，可细分为数值仿真法、半离散法和全离散法等几种方法。时域数值仿真法就是首先对铣削过程中的切削力、扭矩、功率、表面粗糙度及振动量等进行仿真，然后对仿真结果施加某种稳定性判据，最后得到稳定性叶瓣图的方法。Tlusty等采用时域数值仿真方法对铣削过程中的动力学行为进行描述，并研究了稳定区与非稳定区的边界［21］。Smith等采用峰－峰图对铣削时域仿真结果进行评估［22］。Altintas等对插铣过程进行时域仿真，发现扭转－轴向振动是引起加工颤振的主因［23］。Campomanes等建立了面向小径向切深的时域颤振稳定域模型，仿真结果证实了稳定性叶瓣图中附加稳定性叶瓣的存在［24］。时域数值仿真法的一般过程可描述为(见图2)［25］:

(1)建立铣削系统动力学微分方程。

(2)用数值方法求解微分方程。对连续时间进行离散化，根据已知初始条件以一定时间增量对微分方程进行求解。虽然采用近似求解方法，但只要时间增量足够小，便可获得满意的求解精度(Euler法的计算精度是1阶，Runge－Kutta法的计算精度是4阶)。为求解方便可直接调用MATLAB库函数ode45()求取每一离散时刻所对应的位移和速度。

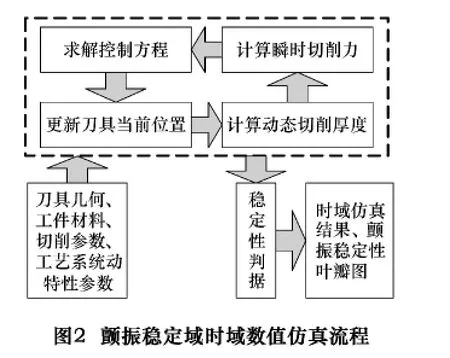
(3)根据微分方程求解结果更新刀具当前位置并对动态切削厚度进行修正。

(4)计算当前时间步下的动态铣削力。

(5)判断仿真是否结束，若未结束跳转到步骤(2)。

(6)对仿真得到的时域数据施加某种稳定性判据确定当前切削条件下的稳定性。

(7)改变主轴转速与轴向切深，重复步骤(2)～(7)获得时域颤振稳定性叶瓣图。

与频域方法不同，采用时域数值仿真法需事先确定稳定性判据。目前主要有以下几种稳定性判据［25］:①FFT法，其基本思想是对时域仿真数据作FFT变换，根据切削频率及其谐振频率下的幅值在所有频率范围的幅值之和中所占比例ηp作为颤振发生的标准，当ηp＜0.8时可认为存在颤振。②PTP法，该方法基于切削条件接近稳定边界时切削力峰值会急剧增大的思想。③动静态力法，将相同切削参数下柔刚性系统的最大切削力之比ηF作为判定标准，当ηF＞1.3时认为存在颤振。④刀尖位移统计方法，该方法由Schmitz提出，铣刀每旋转一周采集一次刀尖位移数据，然后使用其样本统计方差作为颤振判定标准［26］。

时域仿真方法基于所建立的相对真实的切削动力学模型，可以综合考虑诸如刀具几何、刀齿偏心、刀齿因振动脱离切削区、多维结构动力学及非线性过程增益等因素对加工过程稳定性的影响，故预测精度较高［27］。不足之处在于，尽管时域模型非常强大，但目前尚很难找到一种通过仿真数据准确判定系统稳定性的判据。此外，由于它需要针对不同主轴转速、轴向切深进行时域仿真且在时域仿真中需求解微分方程，故其计算量大，计算时间长。

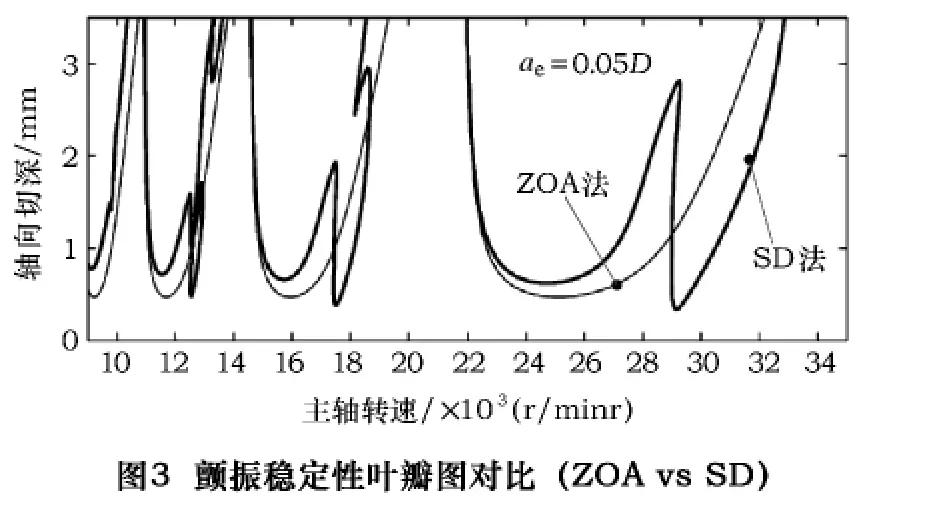
半离散方法(Semi Discretization，SD)由Insperger提出，它在每个离散采样时间间隔里考虑方向力系数的时变性，可以预测任何转速下的稳定性极限［28］。SD方法的精度取决于采样间隔，计算时间取决于加工系统模态阶数及采样间隔。SD方法由于在离散时间间隔Δt考虑了时变、周期因子［A(t)］，其稳定性预测精度更高(尤其是当径向切深较小时)，可揭示周期性稳定运动、准周期性颤振和周期性颤振等3种刀具运动。SD法与ZOA法颤振稳定性仿真结果对比见图3。

全离散方法(Full Discretization，FD)由丁汉等提出［29］，该方法将铣削加工过程的基本数学模型表示为具有单个离散时延的线性时间周期系统，对时间周期进行离散处理，通过直接积分获取系统的响应。在每个小时间间隔内，通过线性插值对系统状态项、时间周期项和时延项等作近似表示。基于获得的单个时间间隔状态变换离散图构建系统变换矩阵的闭式表达式，采用Floquet理论预测系统的稳定性。

FD方法与SD方法的区别在于:①SD方法仅对时延项进行离散处理，而FD方法则通过线性插值对状态项和时延项进行离散处理;②SD方法的周期方向力系数通过求平均值获得，而FD方法的周期方向力系数则通过对时间段的边界值进行插值获得。③获取颤振稳定性叶瓣图时，SD方法需要针对主轴转速和切削深度进行双重循环来计算传递矩阵，而FD方法则只需要针对主轴转速进行单重循环。因此，FD方法可获得与SD方法相同的计算精度，但计算效率要高很多。

3 切削试验法

切削试验法是指通过切削试验获取颤振稳定性叶瓣图的方法。Quintana等采用固定主轴转速、改变轴向切深的方法获得了稳定性叶瓣图［30］，其基本思想是首先固定主轴转速，沿进给方向改变轴向切深，采用麦克风拾取切削噪声，并利用计算机对噪声信号进行采样识别，当颤振发生时停止切削，这样就得到了对应该主轴转速下的极限切深;然后按一定步距逐渐增加主轴转速，重复上述过程，得到每一主轴转速下的极限切深。Yoon等提出了一种基于对实测切削力进行小波变换以确定加工颤振的新方法，该方法得到了FFT方法的验证［31］。Walter等提出根据工件表面粗糙度和采用麦克风测量声音信号的方法来确定加工过程的稳定性 (见图 4)［32］。Somkiat等提出了一种用于判定铣削过程是否发生颤振的新方法，该方法以实测三向切削力均方差的3个比值为判据［33］。刘安民等提出了一种基于建立的铣削系统动力学模型，根据实测得到的颤振频率求解出系统的模态参数与过程参数，进而得到稳定性叶瓣图［34］。

与获取颤振稳定性叶瓣图的其他方法相比，一方面，切削试验法大多针对特定切削条件进行，具有成本高、费时和通用性差等缺陷，很少直接被用来预测稳定性极限。另一方面，由于它是切削条件的真实反映，故被常用来确定其他稳定性极限预测方法是否有效。

4 结论与展望

本文结合国内外研究现状对频域法、时域法和试验法等3类铣削颤振稳定性预测方法进行分析对比，总结了其各自特点和适用场合。频域法尤其是ZOA法计算速度快，其预测精度能满足大部分应用场合;时域法能揭示铣削过程中蕴含的各种动力学现象、预测精度较高，但计算量大;试验法是切削条件的真实反应，但成本高，主要用于验证其他仿真方法的有效性。该领域尚未解决的问题主要存在以下两方面:①时变、非线性、迟滞铣削系统的建模与准确求解;②中低速下过程阻尼建模及考虑非线性阻尼特性的铣削颤振模型。

［1］Tobias S A.Machine tool vibration［M］.Glasgow:Blackie and Sons Ltd，1965.

［2］Koenigsbenger F，Tlusty J.Machine tool structures－ Vol.1:Stability against chatter［M］.New York:Pergamon Press，1967.

［3］Merrit H E.Theory of self－ excited machine tool chatter［J］.ASME Journal of Engineering for Industry，1965，87:447 －454.

［4］Minis I，Yanushevsky T.A new theoretical approach for the prediction of machine tool chatter in milling［J］.ASME Journal of Engineering for Industry，1993，115:1－8.

［5］Budak E.The mechanics and dynamics of milling thin－walled structures［D］.University of British Columbia，1994.

［6］Budak E，Altintas Y.Analytical prediction of chatter stability in milling－part I:general formulation;part II:application to common milling systems［J］.Transactions of ASME，Journal of Dynamic Systems，Measurement and Control，1998，120:22 －36.

［7］Altintas Y，Shamoto E，Lee P，et al.Analytical prediction of stability lobes in ball－ end － milling，transactions of ASME［J］.Journal of Manufacturing Science and Engineering，1999，121:586 －592.

［8］Altintas Y.Analytical prediction of three dimensional chatter stability in milling［J］.Japan Society of Mechanical Engineers，International Journal Series:Mechanical Systems，Machine Elements and Manufacturing，2001，44(3):717 －723.

［9］Merdol S D，Altintas Y.Multi frequency solution of chatter stability for low immersion milling［J］.Journal of Manufacturing Science and Engineering，2004，126:459 －466.

［10］Engin S，Altintas Y.Mechanics and dynamics of general milling cutters Part II:inserted cutters［J］.International Journal of Machine Tools＆ Manufacture，2001，41(15):2213 －2231.

［11］Li Z Q，Liu Q.Modeling and analytical solution of chatter stability for t－ slot milling［J］.Chinese Journal of Mechanics Engineering，2010，23(1):88－93.

［12］Slavicek J.The effect of irregular tooth pitch on stability of milling［C］.Proceedings of the Sixth MTDR Conference，Pergamon Press，London，1965，1:15 －22.

［13］Altintas Y，Engin S，Budak E.Analytical stability prediction and design of variable pitch cutters［J］.Transactions of ASME，Journal of Manufacturing Science and Engineering，1999，121(2):173 －178.

［14］Budak E.An analytical design method for milling cutters with nonconstant pitch to increase stability.Part I:Theory.Part II:application［J］.Transactions of ASME，Journal of Manufacturing Science and Engineering，2003，125(1):29 －38.

［15］Kardes N，Altintas Y.Mechanics and dynamics of the circular milling process［J］.Journal of Manufacturing Science and Engineering，2007，129:21－31.

［16］李忠群，刘强.圆角铣削颤振稳定域建模与仿真研究［J］.中国机械工程学报，2010，46(7):181 －186.

［17］Bravo U，Altuzarra O，Lopez de Lacalle L N，et al.Stability limits of milling considering the flexibility of the work－piece and the machine［J］.International Journal of Machine Tools＆ Manufacture，2005，45(15):1669－1680.

［18］Vincent T，Lionel A，Gilles D，et al.Integration of dynamic behavior variation in the stability lobes method 3D lobes construction and application to thin － walled structure milling［J］.International Journal of Advanced Manufacturing Technology，2006，27(7 －8):638 －644.

［19］李忠群.复杂切削条件高速铣削动力学建模、仿真与切削参数优化研究［D］.北京:北京航空航天大学，2008.

［20］Li Z Q，Liu Q.Impact of modal parameters on milling process chatter stability lobes［J］.Journal of Wuhan University of Technology，2006，28(1):190－195.

［21］Tlusty J，Ismail F.Basic nonlinearity in machine chatter［J］.Annals CIRP，1981，30:21 －25.

［22］Smith S，Tlusty J.Efficient simulation programs for chatter in milling［J］.Annals CIRP，1993，42(1):463 －466.

［23］Ko J H，Altintas Y.Time domain model of plunge milling operation［J］.International Journal of Machine Tools＆ Manufacture，2007，47:1351－1361.

［24］Campomanes M L，Altintas Y.An improved time domain simulation for dynamic milling at small radial immersions［J］.Journal of Manufacturing Science and Engineering，2003，125:417 －422.

［25］Li Z Q，Liu Q.Solution and analysis of chatter stability for end milling in the time － domain［J］.Chinese Journal of Aeronautics，2008，21(2):169－178.

［26］Schmitz T L.Chatter recognition by a statistical evaluation of the synchronously sampled audio signal［J］.Journal of Sound and Vibration，2003，262(3):721 －730.

［27］李忠群，刘强.数控铣削加工过程仿真与优化——建模、算法与工程应用［M］.北京:航空工业出版社，2011.

［28］Insperger T，Stepan G.Updated semi－discretization method for periodic delay － differentilal equations with discrete delay［J］.International Journal for Numerical Methods in Engineering，2004，61:117 －141.

［29］Ding Y，Zhu L M，Ding H，et al.A full－discretization method for prediction of milling stability［J］.International Journal of Machine Tools＆ Manufacture，2010，50(5):502－509.

［30］Quintana G，Ciurana J，Teixidor D.A new experimental methodology for identification of stability lobes diagram in milling operations［J］.International Journal of Machine Tools＆ Manufacture，2008，48:1637－1645.

［31］Yoon M C，Chin D H.Cutting force monitoring in the endmilling operation for chatter detection［J］.Proceedings of the Institution of Mechanical Engineers，Part B:Journal of Engineering Manufacture，2005，219(6):455 －466.

［32］Walter L W，Rolf B S，Milton L P，et.al.Evaluation of high － speed end － milling dynamic stability through audio signal measurements［J］.Journal of Materials Processing Technology，2006，179(1 －3):133 －138.

［33］Somkiat T，Narongsak P.Development of chatter detection in milling processes［J］.International Journal of Advanced Manufacuring Technology，2013，65(5 －8):919 －927.

［34］刘安民，彭程，刘吉兆，等.高速铣削时颤振的诊断和稳定加工区域的预报［J］.机械工程学报.2007，43(1):164－169.