单储丝筒线切割机的切割线振动研究*

张国庆 赵则祥 于贺春 张 洪 张楚鹏

(中原工学院机电学院，河南郑州 451191)

在对特殊晶体进行线切割加工时，切割线的振动和切割方向的频繁改变会对晶体的切割精度造成很大影响。切割线的振动主要由张力波动产生，而引起切割线张力波动的因素有很多，如匀速切割过程中切割阻力的变化、变速切割过程中切割速度的大小和方向的改变以及在整个切割过程中张力调节装置对切割线的影响。对切割线的张力波动进行控制可以减小切割线在工作过程中的振动，进而提高加工精度。张义兵等人［1］分析了张力锤结构对张力波动的影响，并设计了一种对张力波动影响较小的控制系统。蒋近等人［2］提出了减小张力摆杆结构对张力波动影响的方法，并设计了基于相邻轴误差的多电动机同步控制系统。黄洁等人［3］对张力的自适应控制方法进行了仿真研究，设计了一种精度较高的张力控制算法。

在目前已知的张力控制方法中，绝大多数是通过控制非切割区域的张力来间接调节切割区域的张力，而由于切割线导向轮存在转动惯量，使得张力调节出现迟滞，不能达到预期的效果。而针对导向轮转动惯量对切割线振动的影响方面的研究，国内外尚未见报道。本文建立了基于单储丝筒线切割机床走丝系统的数学模型，推导出在切割阻力作用下切割线的长度及弯曲角度的变化公式，在Matlab的Simulink环境下建立仿真模型，并运行求解，结果揭示了导向轮转动惯量和切割阻力对切割线振动的影响规律。

1 走丝系统的总体结构

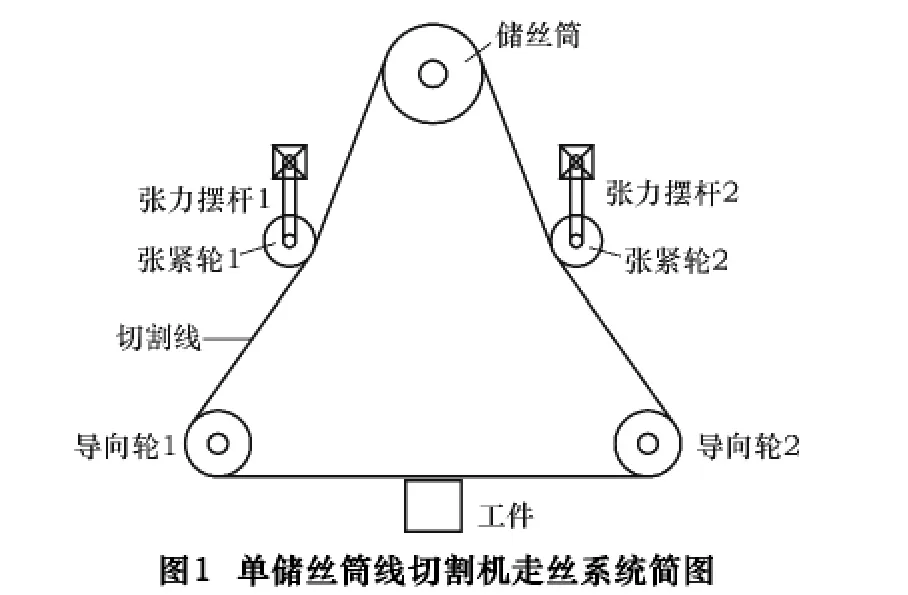
单储丝筒线切割机为单线切割，切割线为金属丝或镀金刚石微粒金属丝，主要用于特殊晶体的切割，对切割质量要求很高。

图1为单储丝筒线切割机走丝系统的结构简图。绝大部分的切割线绕在储丝筒上，其余部分绕过张紧轮、导向轮最后回到储丝筒。切割工件时储丝筒由电动机带动旋转，张紧轮和导向轮在切割线的带动下同时转动，由于受到工件带来的切割阻力的影响，两个导向轮之间的切割线会发生弯曲，两个张力摆杆机构的摆动角度随之改变。

2 转动惯量对切割线振动的影响

由于储丝筒同时完成收放线工作，在假设切割线不可延长的前提下，未被缠绕在储丝筒上线的总长度保持不变。在匀速切割过程中，如果没有切割阻力，则各导向轮和张紧轮的转速恒定且张力摆杆的摆动角度不变，切割线的张力处处相等，走丝系统处于一个相对稳定的状态。而由于两个导向轮之间的切割线在切割工件时受到切割阻力，使得此段切割线的张力增大，大于储丝筒与导向轮之间切割线的张力，导向轮由于受力不均转速发生改变。两个导向轮之间的切割线的长度增加，则储丝筒与导线轮之间的切割线的长度同时减小。

在不考虑各轮转动摩擦力和切割线重力的前提下，如果张紧轮和导向轮的转动惯量为零，则两个导向轮之间的切割线的张力变化能在瞬间传到储丝筒与导向轮之间的切割线上，使得各处张力同时变化且处处相等。由于转动惯量的存在，使得张力的传递出现了迟滞，成为引起切割线振动的一个主要因素。

3 转动惯量的分析模型

3.1 数学模型的建立与分析

为了分析转动惯量对切割线振动的影响，本文建立了一个走丝系统的简化的模型，如图2所示。为简化后期计算，模型中设定储丝筒与两个导向轮的直径相等，用理想的恒力FP代替张力摆杆装置，FP作用在储丝筒与导向轮之间切割线的中点上，方向垂直于储丝筒与导向轮的中心连线。模型中将工件带来的切割阻力简化为一个方向垂直向上的变力FM，FM作用在两个导向轮之间切割线的中点上，其大小模拟真实情况下的切割阻力。储丝筒与导向轮的中心距记为L，两个导向轮之间的中心距记为L＇。

初始状态下，此模型中储丝筒和导向轮均静止，切割阻力FM为零，储丝筒与导向轮之间的切割线在恒力FP的作用下达到最大弯曲程度，两个导向轮之间的线无弯曲，切割线的张力处处相等。之后随着FM的变化，各段切割线的长度和张力均发生变化。

图3为储丝筒部分的分析示意图。图中线段AB为储丝筒与导向轮1的公切线上的一段，A点为切点。C点为切割线与储丝筒的切点，D点为恒力FP的作用点，储丝筒与导向轮间的切割线的拉力记为FT，弧AC为切割线缠绕在储丝筒上的部分，切割线线段CD与AB的夹角为α，储丝筒的半径记为r。

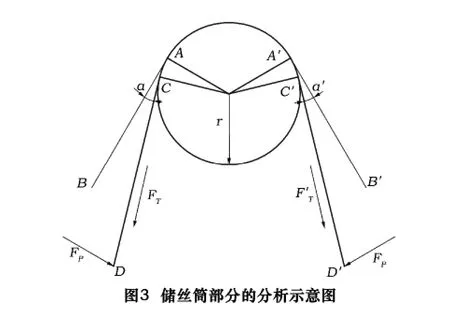
图4为导向轮1部分的分析示意图，字符的定义方法与图3类似。由于在此模型中，导向轮1与2的受力情况相同，故本文中只对导向轮1做分析。

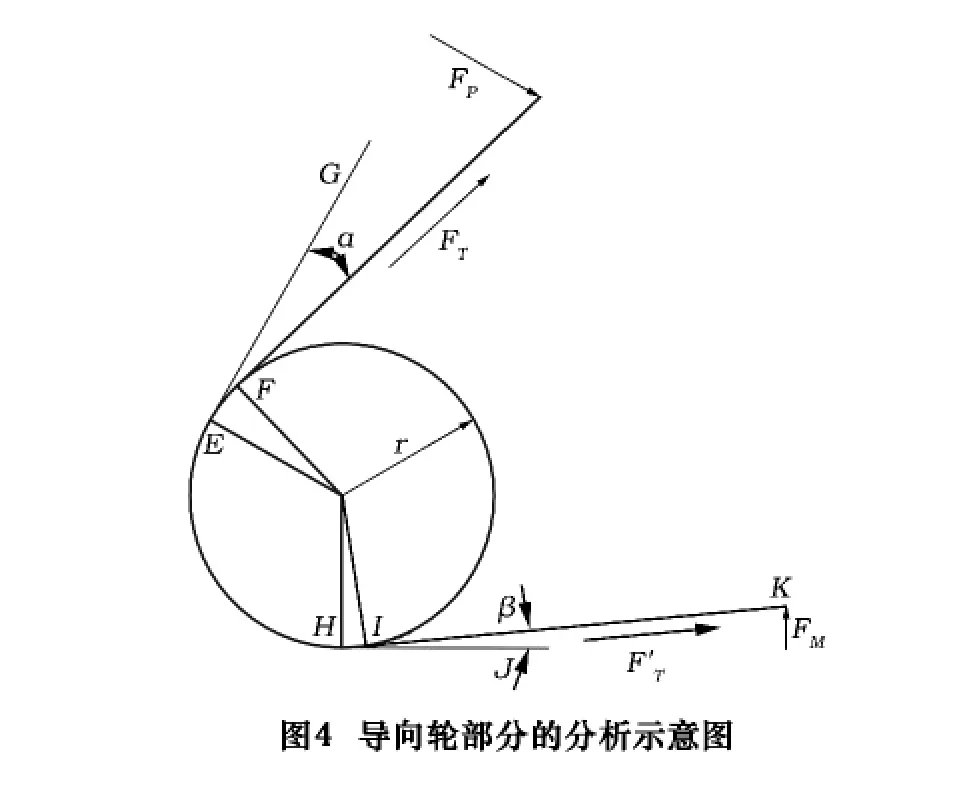
储丝筒与导向轮1的公切线的切点间的切割线的长度为

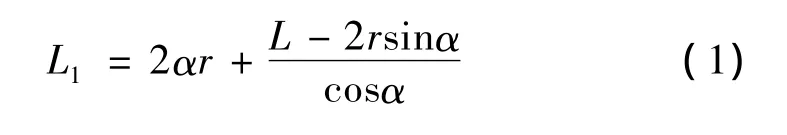
两个导向轮间的切割线的长度为

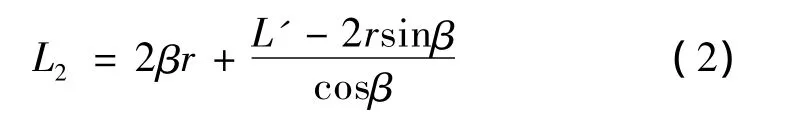
式中:α和β的单位均为rad。

适用于导向轮的转动惯量公式为

使导向轮转动的力为

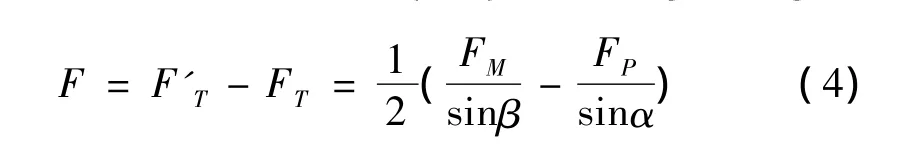
则导向轮转动的线加速度为

在此模型中，随着切割阻力FM的变化，各部分切割线的弯曲角度α和β也会变化。设在t时刻，α和β的大小分别为αt和βt，导向轮的转速为vt，经过Δt时刻之后，α 和 β 的大小分别为 αΔt和 βΔt。设 Δt为无穷小，则在此段时间内，导向轮转动的弧长为

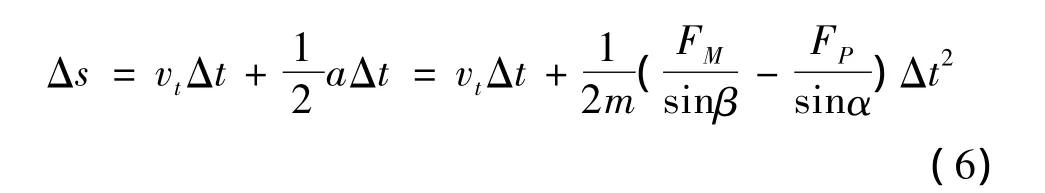
设在t时刻，储丝筒与导向轮之间切割线的总长度为L1t，两个导向轮之间切割丝的总长度为L2t，到t+ Δt时刻切割线的长度分别变为L1Δt和L2Δt，则有

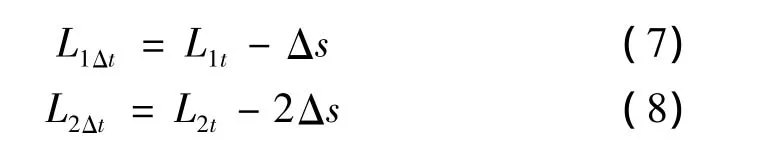
结合公式(1)、(2)、(7)、(8)可得

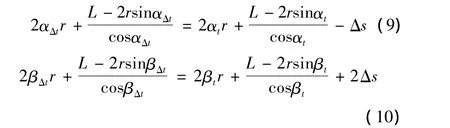
式(9)和(10)反映了导向轮的转动对切割线弯曲角度的影响，而导向轮的转动规律由切割阻力FM决定，利用Simulink的动态仿真功能可以得出在FM作用下的导向轮转动惯量对切割线振动的影响。

3.2 Simulink仿真模型的建立与分析

根据式(6)、(9)、(10)建立的Simulink仿真模型如图5所示。在此模型中设定输入的切割阻力及其他相关参数，运行求解后即可得出导向轮转动惯量对切割线振动的影响。

4 运行求解

4.1 初始条件的设定

结合实际情况，在运行求解前将初始条件设定为:L=1.2 m，L′=1.0 m，r=0.1 m，m=0.1 kg，α =π/18，β=0。FM输入的是一个半周期正弦波，其振幅为20，频率为1/1 200，仿真求解时间为600 s。

4.2 仿真结果

Simulink模型运行后，各示波器输出的波形如图6所示。

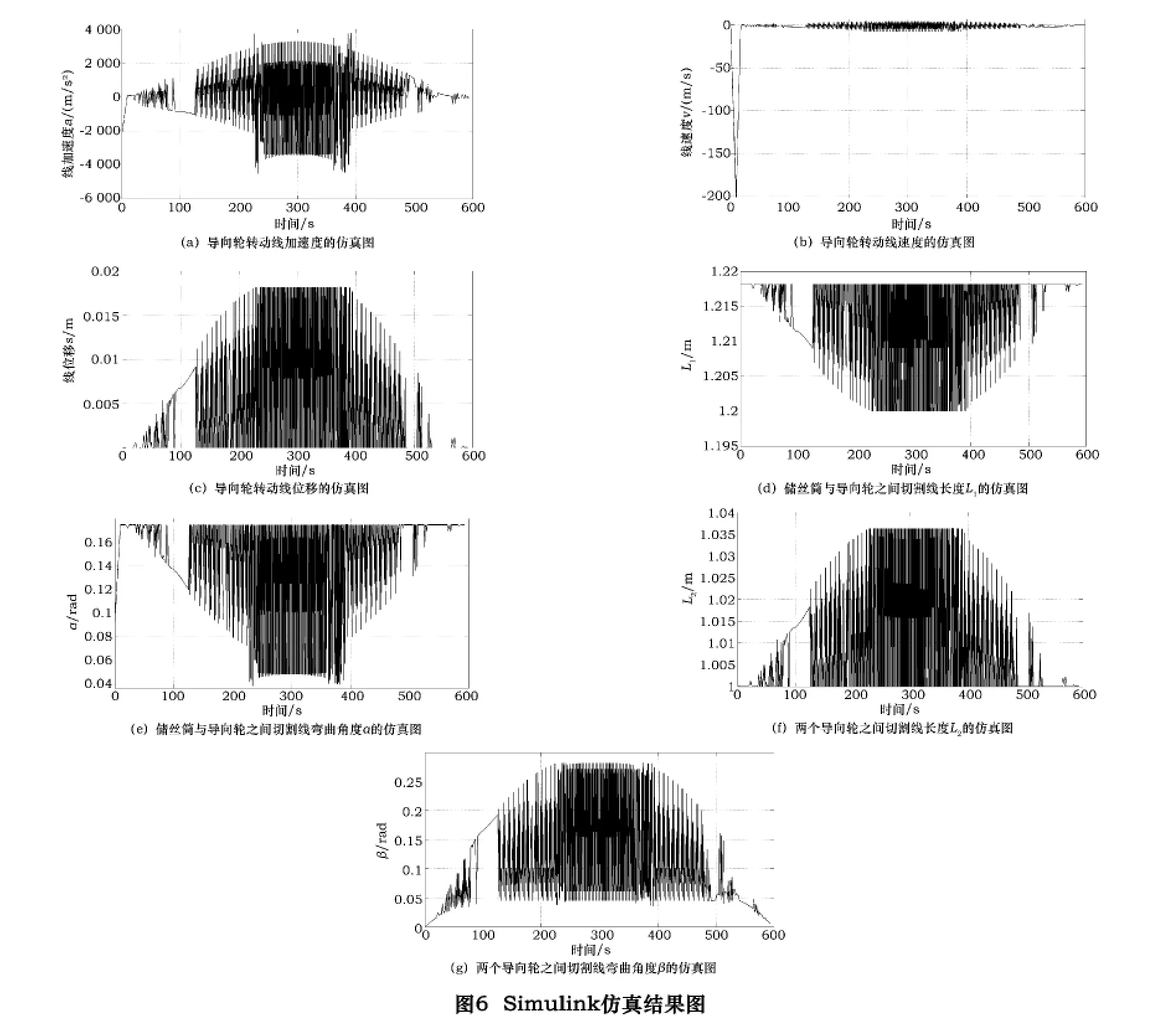
由图6可以看出，导向轮在切割线的带动下其线加速度、线速度和线位移时刻发生着变化，同时两个导线轮之间的切割线的弯曲角度β也在不断变化。角度β的变化反映了切割线的振动情况，其变化趋势与切割阻力的变化趋势大体一致，其幅值与导向轮质量近似成反比关系。

5 结语

(1)导向轮转动惯量的存在是切割线在工作过程中发生振动的主要原因。

(2)切割阻力的变化规律对切割线的振动规律有决定作用。

(3)减轻导向轮的重量可以提高切割线振动的灵敏度，虽然此时切割线振动频率更高，但是振幅会减小，在实际加工过程中更有利于提高工件表面质量。

［1］张义兵，戴瑜兴，袁巨龙，等.多线切割机线张力控制系统设计实现［J］.机械工程学报，2009，45(5):295 －300.

［2］蒋近，戴瑜兴，郜克存，等.多线切割机线走线系统的张力控制［J］.机械工程学报，2011，47(5):183 －187.

［3］黄洁，李伟.多线切割机线张力自适应控制仿真研究［J］.机械科学与技术，2012，31(3):437 －441.