基于声发射信号的铣削加工表面粗糙度**1预测技术研究
熊 巍 李郝林
(①上海理工大学机械工程学院,上海 200093;②上海理工大学材料科学与工程学院,上海 200093)
铣削加工表面粗糙度是衡量铣削加工质量的主要指标之一,加工出合格的零件除了有合格的尺寸精度外,还需获得与零件图纸一致的表面粗糙度。
目前,对于铣削加工中粗糙度预测的研究主要可以分两大类方法,基于切削理论的数学模型法和实验法[1]。但是,由于影响加工表面粗糙度的因素很多,所以,前者很难得到非常精确的计算值,并且很多的系数同样依赖实验,而后者其可重复性较差,往往只能适用于一种刀具或一台机床。Yu-Hsuan Tsai等人[2]运用加速度仪和位移传感器提出了在线检测粗糙度的技术,其运用模糊理论根据实验所得数据建立了在线识别的数学模型用于在线测量加工铝合金时的粗糙度。但是他并没有从切削机理出发,研究不同的信号特征与粗糙度之间的联系,其结果也只能用于切削铝合金一种材料。
声发射技术,近年来越来越多地运用于监测加工切削过程中,迟玉伦[3-4]等人利用声发射监测磨削加工,汤为[5]利用声发射信号来监测刀具磨损,N.-C.Tsai[6]等人将声发射用于监测铣削颤振。但是,刀具磨损不等于产品不合格,而没有发生颤振也不等于产品合格。
因此,本文着力于利用声发射测量材料变形时发出的能量特性,根据切削机理,研究根据识别声发射信号的特征,预测铣削表面粗糙度的方法。

1 铣削表面粗糙度的形成
铣削加工过程是一个由多齿参与的断续切削过程,铣刀随机床主轴绕自身轴线回转而工件相对于铣刀作进给运动[7],如图1所示。如不计其他各种因素,铣削后的粗糙度与每齿进给量f有关系。图2以两刃铣刀为例,根据图示,铣削后的粗糙度由两齿间的残留高度所决定,其计算公式如下:
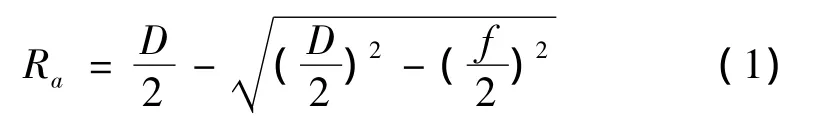
式中:D为刀具的直径。
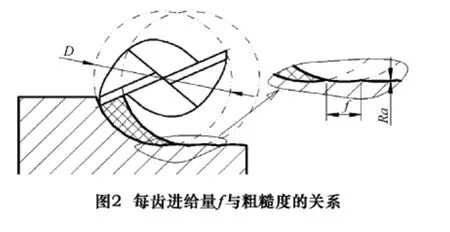
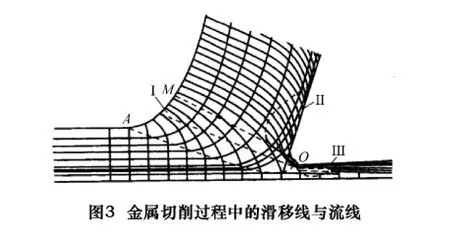
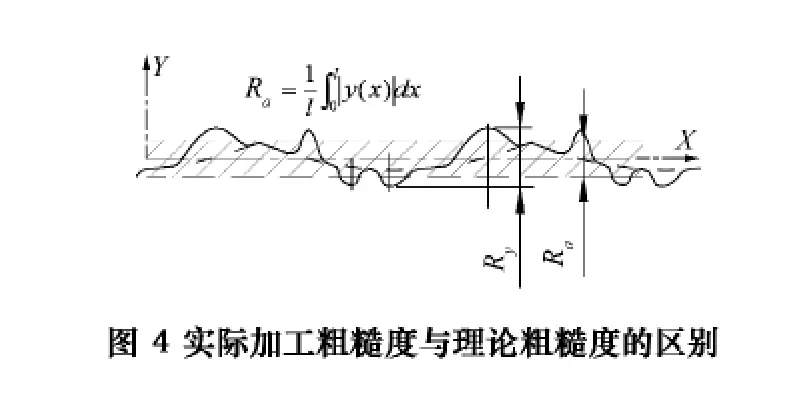
但是,被切部分材料受刀具挤压破坏从工件上剥离并不是连续、光滑、均匀的。切削过程中会发生剪切和滑移变形,从图3可以看出,Ⅰ区处的材料晶粒会发生剪切滑移变形,由于材料的不均匀性,切屑的不连续性以及Ⅱ区切屑与刀具前刀面的摩擦等使切削力产生变动,使刀具、工件的弹性位移发生变化;加之机床主轴轴承回转精度及各滑动导轨面的形状误差等使运动机构发生跳动等等这些因素,会使切屑厚度发生变化[8],形成表面不平度。以及Ⅲ区处已加工表面与刀具后刀面的挤压摩擦,会使已加工面产生变形和回弹[7],进一步地增加表面的不平度。从图4可以看出,在一次切削时,由于切屑厚度的变化,会在原先的切削表面上留下凹凸不平的痕迹,有时凸起,有时凹陷,这些痕迹构成了表面不平度,从而最终形成粗糙度。目前,用于评价粗糙度值的参数主要有两种,一种称为轮廓最大高度Ry,另一种称为轮廓算术平均偏差Ra,而在工程上,Ra使用的最为广泛。
2 声发射信号
根据上述的分析,不难发现,通过检测加工过程中切屑厚度的变化,使之与理论切屑厚度进行相比较,就可以有效地预测加工的粗糙度。
声发射是在金属加工中分子晶格发生位错、裂纹扩展及塑性变形时释放出的一种超高频应力波脉冲信号[5]。声发射的特点就是直接测量材料变形时发出的能量,相对于加速传感器来说,更为直接地反映材料在切削变形中的情况,其对切屑厚度的变化比其他各种传感器更为敏感。E.SUSIC[9]等人提出了利用声发射信号在线预测摩擦过程中被摩擦材料的粗糙度变化。
3 实验设计
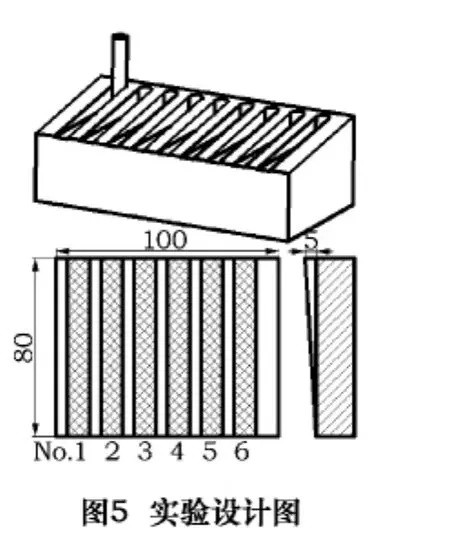
在之前的分析中提到加工表面粗糙度理论上应该由每齿进给量f和铣刀直径D所决定了,与其他参数无关。所以,在所设计实验中,这两个参数,始终不发生改变,而主要改变主轴的转速(即切削速度)和切削深度。由此,参考 Guillem Quintana[10]等人的实验方案,设计了用直径为10 mm的2刃平底螺旋立铣刀以不同的主轴转速在斜面上切除一条条槽,如图5所示,工件长100 mm宽80 mm,切深从0 mm逐渐增加到5 mm,以每齿切0.06 mm的进给量进行切削。具体切削参数详见表1。
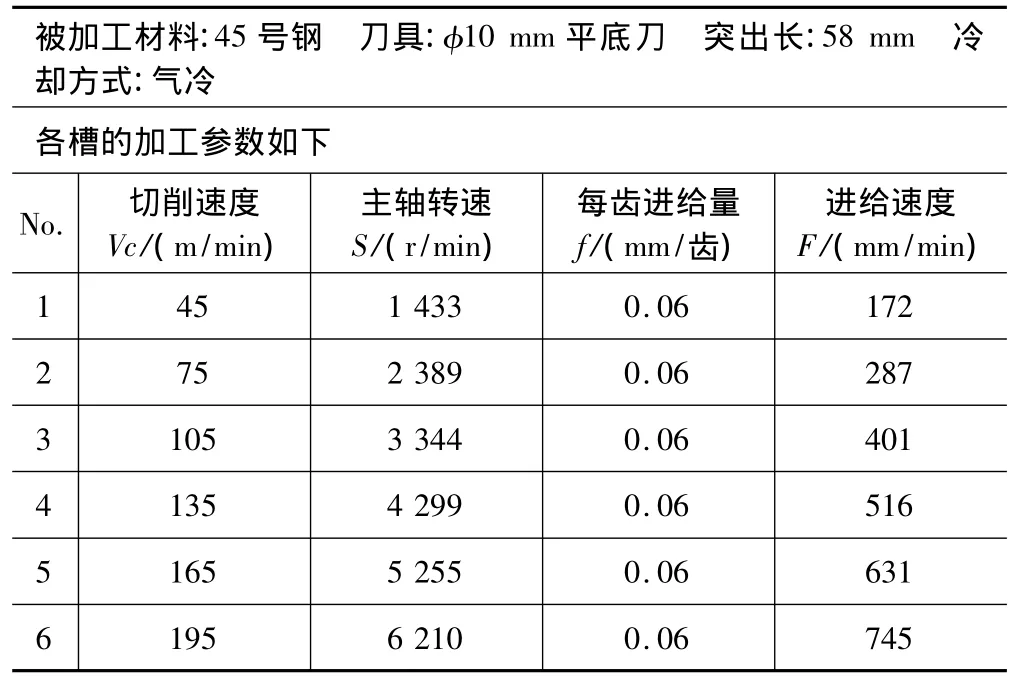
表1 实验加工参数表
4 理论切屑厚度的计算
根据前面的分析,在线预测加工粗糙度最重要的就是要将实测信号与理论切屑厚度曲线进行相比较。理论切屑厚度的计算,就是不考虑任何切削振动、变形等因素时,刀具理想切削状态下的切屑厚度变化情况。也就是说,此时的加工表面粗糙度可以由式1计算得到,本次实验的每齿进给量f为0.06 mm/齿,根据试1,其理论粗糙度Ra为 0.09 μm。
刘强[7]等人给出了平底铣刀瞬时切屑厚度的计算公式为:
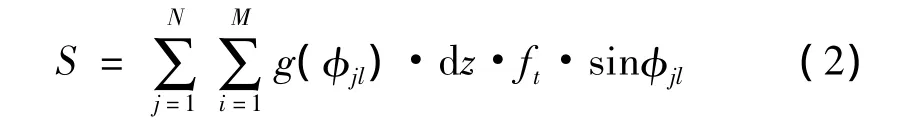
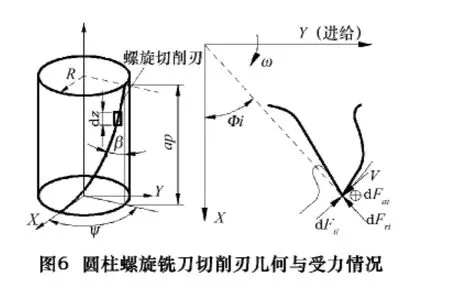
如图6所示,式中:dz为沿铣刀轴线方向上的切削刃微元,在Z轴方向将切削刃分成M个微元;ft为铣刀每齿的进给量;N为刀具的刃数;φjl为第j个刀齿上第l个切削刃微元处的瞬间径向接触角,其定义为:

式中:φ10为第一个切削刃端点处的角位移;β为刀具的螺旋角;R为刀具的半径;g(φjl)为单位阶跃函数用于表示当前切削刃微元是否参与切削,其定义为:

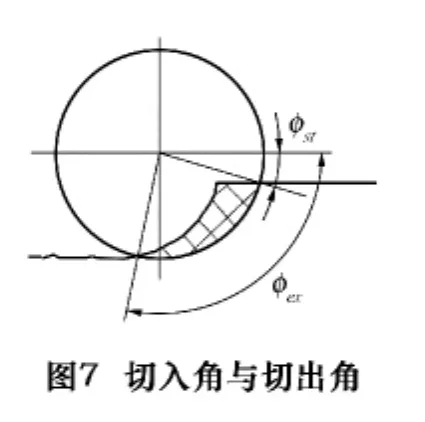
φst,φex分别表示切入角和切出角。如图7所示。
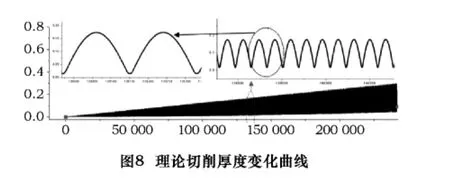
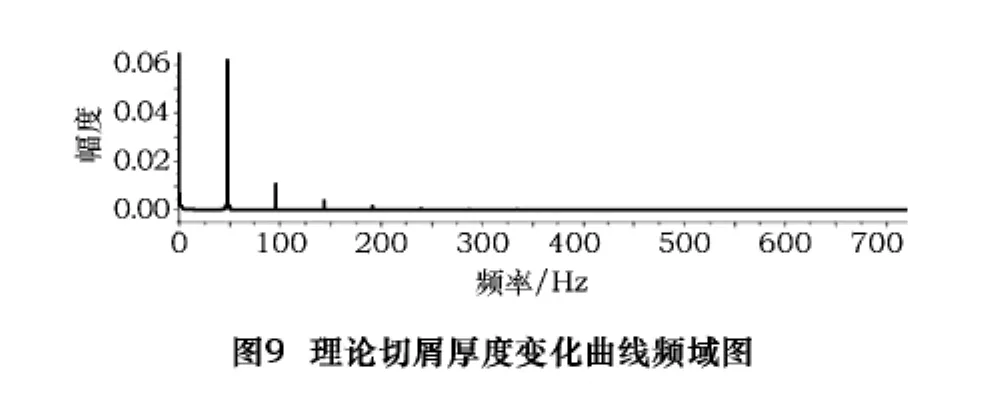
根据上述计算公式对本次实验的理论切屑厚度进行了计算,运用 Matlab编程,计算得到了这次实验的理论切屑厚度变化曲线,如图8所示,从所得到的曲线来看,铣削明显呈断续加工状态。以主轴转速S为1 433 r/min为例,运用傅立叶变换来分析它的频域特性,得到其频域特性图,如图9所示:因为主轴转速S为1 433 r/min,刀具使用的2刃刀具,所以刀具切削的频率应该是47.8 Hz(转速÷60×刃数)。根据频域图可以看到,频率47.8 Hz的幅度最大为0.06,二阶谐振频率95.6 Hz的幅度为0.01,三阶谐振频率143.3 Hz的幅度为0.004。值的注意的是,幅度值的大小和单位,与信号源,以及采样数有关系,很难有客观的参考价值,但是分析不同频率下的幅度值占总幅度值的比例却有很大的参考价值。因此,幅度采用无量纲,进一步分析可以发现,其主要的切削能量集中在刀具的切削频率上,占了全部能量的80%以上,而在二阶和三阶的谐振频率上的能量分别是切削频率上能量的1/6和1/15。而在其他频率上的能量几乎为零。
5 实验数据分析
实验现场的照片如图10所示,实验使用的是沈阳机床厂的VMC850立式铣床(FANUC系统)。声发射的探头分别安装在工件的两边,如图11所示,声发射波会沿工件表面传递到传感器上[9]。实验过程中,通过信号采集卡和计算机记录下了切削过程中的声发射信号,并测得了加工后的表面粗糙度。



由于存在着种种的影响因素,切屑厚度曲线不可能像理论曲线那样光滑,而这些不光滑度所反映的切屑厚度变化应该与表面的粗糙度有着密切的关系。图12是同样以主轴转速S为1 433 r/min切削时的声发射信号。
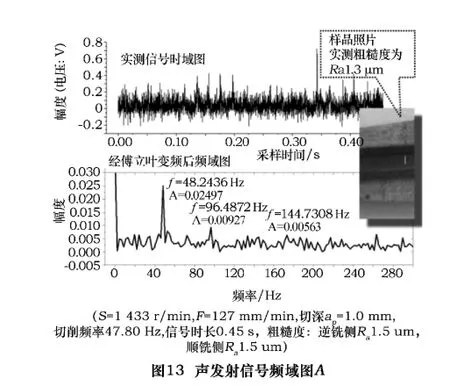
可以看到,声发射信号与理论切屑厚度曲线相比,其信号曲线不光滑,存在着许多的高频信号。从理论的切屑厚度曲线的频域图来看,理想的切削状态,其主要的切削能量应该集中在切削频率上。而声发射信号的频域分析显示出,声发射的频域关系与加工粗糙度有着密切的关系。图13、14、15分别是3个不同粗糙度值下的频域图。
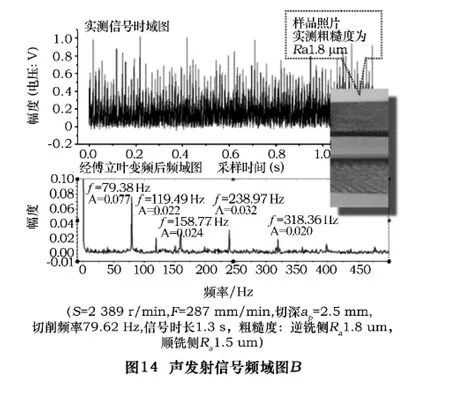

表2 实验中所测得声发射(AE)信号与粗糙度的对应表 μm
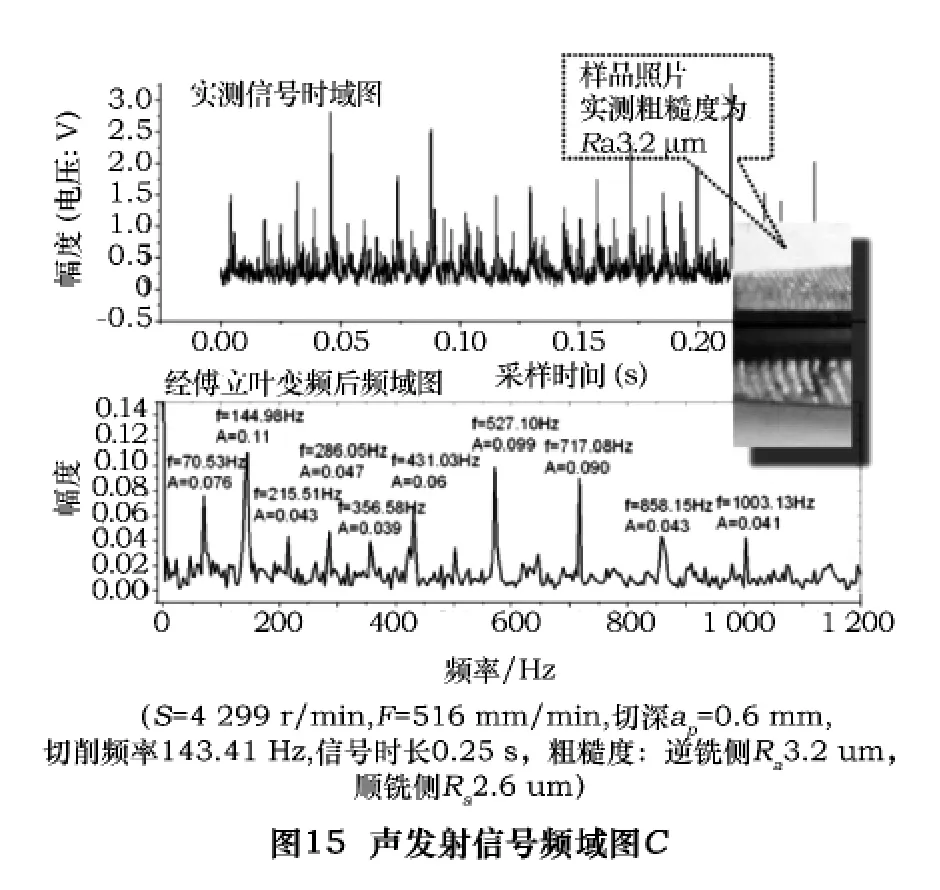
通过比较这3组图与理论切屑厚度频域图之后,可以发现,切削能量越集中在主频上,其加工粗糙度就越好,而能量越分散,其粗糙度就越差。同时,在图12中,近1.5倍的主频处(119.486 Hz)有明显的切削能量,说明此时两齿切削并不平衡,一个齿切了多一点,一个齿切了少一点,刀具切削时有颤振发生,从样品的照片上也可以看出顺铣处有明显的振纹留在切削表面上。图13呈现了一个比较恶劣的切削状态,其主频上的能量不到全部能量的16%,同时,0.5,1.5,2.5倍主频处有很大的能量,两齿切削不一至,有颤振,从样品的照片上也可以看出这一点。表2是实验中所测得的声发射信号与所测得粗糙度的对应表。通过分析,可以发现其中主频能量在整个能量中所占的比例与粗糙度有着密切的关系。通过对表2的总结,得出了主频能量比与粗糙度的关系,详见表3。
6 结语
综上所述,本文通过理论和实验分析验证了利用声发射信号预测加工表面粗糙度的可行性以及预测的方法。从以上的分析以及实验数据可以得出以下结论:即铣削过程中,最理想的切削状态是所有的切削能量都集中在切削频率上,但是,从实际的切削情况来看,由于切削振动等种种因素存在,铣削的能量不可能全部集中在主频上,而分布在其他频率上的能量与主频上的能量比与切削后表面的粗糙度有着密切的联系。
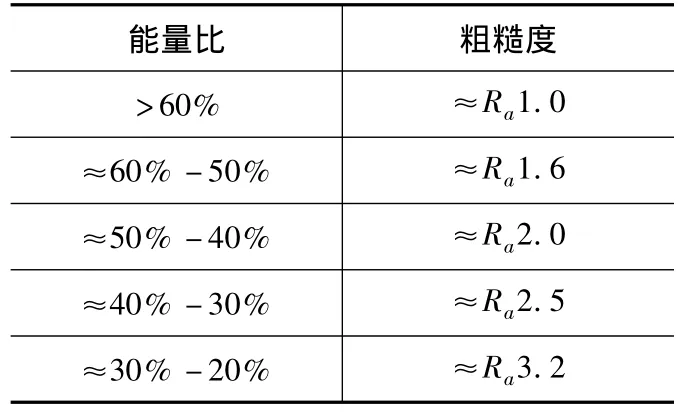
表3 主频能量比与粗糙度的关系
[1]Benardos P G,Vosniakos G C.Predicting surface roughness in machining:a review[J].International Journal of Machine Tools& Manufacture 2003,43(8):833 –844.
[2]Tsai Yu-Hsuan,Chen Joseph C,Lou Shi-Jer.An in-process surface recognition system based on neural networks in end milling cutting operations[J].International Journal of Machine Tools & Manufacture,1999,39(4):583 –605.
[3]迟玉伦,李郝林.基于最大熵的磨削状态判别方法[J].现代制造工程,2010(12):81-83.
[4]迟玉伦,李郝林.光学玻璃磨削状态的声发射监测技术[J].制造业自动化,2010(10):10-13.
[5]汤为.基于声发射法的铣刀磨损状态识别研究[D].上海:上海交通大学,2009:2.
[6]Tsai N C,Chen D C,Lee R M.Chatter prevention for milling process by acoustic signal feedback[J].International Journal of Advanced Manufacturing Technology,2010,47(9/12):1013 -1021.
[7]刘强,李忠群.数控铣削加工过程仿真与优化-建模、算法与工程应用[M].北京:航空工业出版社,2011.
[8]臼井英治(日).切削磨削加工学[M].高希正,刘德忠(译).北京:机械工业出版社,1982.
[9]Susic E,Grabec I.Application of a neural network to the estimation of surface roughness from AE signals generated by friction process[J].Int.J.Mach.Tools Manufact.,1995,35(8):1077 -1086.
[10]Quintana G,Ciurana J,Teixidor D.A new experimental methodology for identification of stability lobes diagram in milling operations[J].International Journal of Machine Tools and Manufacture,2008,48(15):1637-1645.

