材料性能和相对壁厚对管材助推弯曲影响的分析

樊子天，鄂大辛，陈吉生

(北京理工大学材料学院，北京 100081)

管材因具有质量轻，强韧性好，吸收冲击性能好等优点，在航空航天、汽车制造领域中的应用越来越广泛。由于在管材塑性弯曲中的弯管横截面畸变和壁厚减薄规律一直没能被很好掌握，因而阻碍了管材精确弯曲和数控弯曲技术的发展。根据管材力学性能和变形几何条件，正确使用压紧块或尾部助推装置可以有效减轻弯管横截面畸变和壁厚减薄程度。由此，不同的材料性能和变形条件对管材助推弯曲的影响，已成为管材精确弯曲和数控弯曲技术领域中一个重要的研究课题。

文中在实验的基础上，借助于有限元方法，仅在压紧块助推条件下，研究了3种材料和不同相对壁厚管材的助推弯曲对横截面畸变和壁厚减薄的影响，为管材弯曲生产提供参考。

1 实验条件与有限元建模

1.1 实验条件

实验用管材为1Cr18Ni9Ti，TA0(工业纯钛)和5A03(防锈铝)，管外径 d0=20 mm，管壁厚 t0=2 mm，弯模半径R=50 mm，弯曲角度θ=180°。弯曲实验利用VB-200数控弯管机完成。实验前对管材的几何尺寸、平行度及圆度等进行测量并筛选。弯曲成形后，利用线切割方法切割试样，测量并计算壁厚减薄率和短轴变化率。

为了分析管形状态下材料力学性能对助推弯曲的影响，对部分管材进行直接拉伸试验，供理论研究和有限元分析使用，测得真实应力应变σ-ε曲线如图1所示。测算得出的材料力学性能参数见表1。

图1 材拉伸状态下真实应力应变曲线Fig.1 True stress-strain relation for different tubes

表1 不同管材的力学性能参数Table1 Mechanical property parameters for different tubes

1.2 有限元建模

为了提高有限元分析精度，直接加载时的硬化条件、变形条件、工艺参数的定义条件与得到真实σ-ε曲线的拉伸试验条件完全相同。

图2 管材弯曲有限元模型Fig.2 Finite element model of tube rotary draw bending

在DYNAFORM软件中建立管材弯曲的三维有限元模型，如图2所示。管材选用薄壳单元，厚度方向设7个积分点，弯模、夹紧模、弯模镶块、压紧块和防皱块简化为刚性单元。管坯与模具的接触方式为面-面接触，静摩擦系数为 μs=0.15，动摩擦系数为μd=0.1。为防止相对滑动，夹紧模、弯模镶块和管坯之间采用零间隙配合，其余模具工作表面与管坯之间的单边间隙为0.1 mm。有限元采用基于中心差分法的动态显式时间积分算法和静态隐式算法。并使用LS-DYNA非线性动力有限元求解器进行显式成形仿真。

2 结果与讨论

2.1 材料性能对管材助推弯曲成形缺陷的影响

2.1.1 弯管壁厚减薄

管材弯曲变形过程中，弯管内侧壁的增厚直接影响输送流体的流速和压力的稳定性，外侧壁厚减薄则降低承载能力，因此需要严格控制。在工程中，通常采用壁厚减薄率η表示弯管壁厚减薄程度:

式中:t0，t——弯曲前、后管壁厚度，mm。

设管材弯曲前、后纵向线长度分别为l0和l，则弯曲切线方向和半径方向的应变可分别表示为εθ=ln(l/l0)和 εr=ln(t/t0)。如果认为 εθ= －(εφ+εr)，在未产生横截面畸变时，最内、最外侧某一小区域中符合εφ=εr的轴对称变形，因而有:

将按上述简化公式计算的结果与3种管材有助推弯曲和无助推弯曲的壁厚减薄率分布如图3所示，并与实测值进行比较，发现存在一定误差，主要原因是没有考虑材料力学性能参数及其切向弯曲变形方式的影响。

图3 不同材料助推前后的壁厚减薄率Fig.3 Wall thinning ratio before and after boosting bending

由此，针对弯管外侧变形特点，引入材料修正系数ξ，则管壁厚减薄率可表示为:

通过大量管材弯曲实验验证，确定了1Cr18Ni9Ti，5A03及TA0的材料修正系数ξ值分别为 0.510，1.595，1.322。与部分不同规格管材弯曲试验进行比较，计算结果与测试值大致吻合。ξ的赋值原则主要根据表1所示的材料参数而定，由于计算式中没能考虑其他材料性能参数和变形条件的影响，存在一定缺陷，需要修正。该公式可用于粗略估计弯管壁厚减薄率的大小，对管材弯曲生产具有一定的参考价值。

由图3可知，助推弯曲使壁厚减薄率η有所减小，1Cr18Ni9Ti，5A03，TA0 管材助推前后最大壁厚减薄率 ηmax的绝对差值分别为 1.31%，1.36%，2.04%。由表 1 可知，1Cr18Ni9Ti，5A03，TA0 的屈强比 σs/σb分别为 0.28，0.38，0.56，硬化指数 n 分别为0.42，0.30，0.18，即1Cr18Ni9T 硬化最为严重，近似线性硬化，TA0硬化程度最弱，类似理想弹塑性材料。由此可见，屈服后TA0最易变形，5A03变形能力稍低于TA0，1Cr18Ni9Ti最难变形，故有|η|TA0＞ |η|5A03＞ |η|1Cr18Ni9Ti。单纯从管壁厚减薄来看，压紧块同步助推有利于缓解弯管外凸侧切向拉伸变形，但助推效果因材料性能不同略有差异。

2.1.2 弯管横截面畸变

管材弯曲成形中，在弯曲切向拉应力作用下处于自由状态的外凸侧管壁材料具有向弯曲中心方向移动的趋势，使弯曲半径方向的管外径减小，使弯管横截面扁化变形。这将直接导致压力流体输送用弯管产生局部压力损失和流量脉动。由此，通常将短轴变化率φs作为表征弯管横截面畸变程度的重要缺陷指标。

式中:dmin为弯曲成形后管材横截面内的最小直径。

图4所示为有限元模拟三种管材弯曲助推前、后短轴变化率差值 Δφ 分布(Δφ =φs－φa，φa为助推后的短轴变化率)。由图4可见，助推弯曲使3种管材Δφ增大，即减小了横截面扁化变形。Δφ的分布规律与φs相似，即始弯端的Δφ小于终弯端，这是由于整个弯曲过程中始弯端始终受到夹紧模的夹持约束作用，变形较小。此外，由于1Cr18Ni9Ti的伸长率δ和硬化指数n值较大，较好的延伸性和较强的变形抵抗能力使其Δφ均明显大于其他2种材料，即相同的助推工艺对缓解1Cr18Ni9Ti弯管的横截面畸变有更加明显的作用。

图4 助推前后短轴变化率差值有限元结果Fig.4 Finite element results of minor axis change rate difference

2.2 相对壁厚对管材助推弯曲成形缺陷的影响

工程中通常采用相对壁厚t0/d0来描述管材的几何特征，t0/d0不仅表征管材自身的横截面刚度，还可间接反映其对弯曲变形的抵抗能力。为了加深了解助推工艺对弯管成形缺陷的影响，需要研究不同t0/d0条件下管材常规弯曲和助推弯曲时壁厚减薄及横截面畸变的变化情况。

2.2.1 弯管壁厚减薄

不同t0/d0的1Cr18Ni9Ti管弯曲时，助推前、助推后壁厚减薄变化率的有限元计算结果如图5所示。由图5可见，壁厚减薄率η随t0/d0减小而增大。另外，其他变形条件相同时，助推工艺能有效地缓解弯管外侧壁厚减薄程度，且助推前、助推后η的减幅也随t0/d0减小而增大，即助推对减轻壁厚减薄的效果随 t0/d0减小而愈明显。当 t0/d0由0.167减小至0.083 时，相应的 η 最大减幅由1.30%增至2.96%。分析认为，在管壁厚t0一定的情况下，管径d0越大，弯管的抗失稳能力及相对变形刚度越差，总变形量中的塑性成分越大，因此，t0/d0越小，η越大，变形敏感性也逐渐提高，从而使得助推效果更加显著。

图5 不同相对壁厚助推前后壁厚减薄率有限元结果Fig.5 Finite element results of wall thinning ratio for tubes with different relative wall thicknesses before and after boosting bending

2.2.2 弯管横截面畸变

不同t0/d0下1Cr18Ni9Ti管材助推前、后短轴变化率差值Δφ的有限元计算曲线如图6所示。与弯管外壁减薄变化趋势类似，随t0/d0不断减小，Δφ逐渐增加，即截面畸变缓和程度越来越明显。分析认为，弯曲变形程度一定的情况下，即相对弯曲半径R/d0不变，减小t0/d0使得弯曲中性层附近的弹性区变形体积减小，增大总变形量中塑性变形成分，使弯管进一步发生变形而增大截面畸变程度。当t0/d0由0.166 减至0.084 时，Δφmax由1.81%增至3.43%，而Δφ增幅则逐渐减小。由此，对于部分大直径管径，助推工艺能够有效地改善截面畸变程度，但随管径增大，其助推效果逐渐减弱。

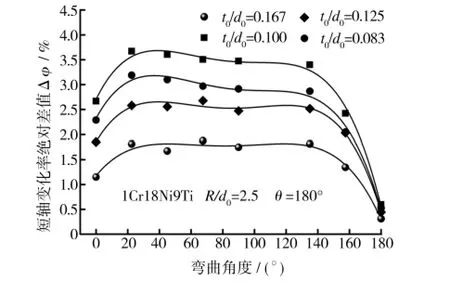
图6 不同相对壁厚助推前后短轴变化率差值的有限元结果Fig.6 Finite element results of minor axis change rate difference for tubes with different relative wall thicknesses before and after boosting bending

3 结语

1)由于壁厚减薄率简化公式仅考虑断后伸长率而未考虑其它材料力学性能参数的综合影响，使得计算值与实测值存在一定误差。引入材料修正系数后，计算值与实测值吻合良好，可用于粗略估计弯管壁厚减薄率的大小。

2)对于不同材料的管材，压紧块同步助推有利于缓解横截面畸变，减小弯管外凸侧切向拉伸变形，但助推效果因材料性能不同而略有差异，相同的助推工艺对缓解1Cr18Ni9Ti管的截面畸变有更加明显的作用。

3)不同相对壁厚t0/d0的管材，压紧块同步助推对壁厚减薄的影响效果随t0/d0减小而明显降低。对于大直径管材，工程中采用助推工艺不能明显改善壁厚减薄程度，但能够有效地改善弯管截面畸变程度。

[1]MEGHARBEL A E，NASSER G A E，DOMIATY A E.Bending of Tube and Section Made of Strain-hardening Materials[J].Journal of Materials Processing Technology，2008，203:372 －380.

[2]MURATA M，KUBOKI T，TAKAHASHI K，et al.Effect of Hardening Exponent on Tube Bending[J].Journal of Materials Processing Technology，2008，201:189 －192.

[3]LI H，YANG H，ZHAN M，et al.Deformation Behaviors of Thin-walled Tube in Rotary Draw Bending under Push Assistant Loading Conditions[J].Journal of Materials Processing Technology，2010，210:143 －158.

[4]E Da-xin，CHEN Ji-sheng，DING Jie，et al.In-Plane Strain Solution of Stress and Defects of Tube Bending with Exponential Hardening Law[J].Mechanics Based Design and Structure，2012，40:257 －276.

[5]E Da-xin，GUAN Z P，CHEN J S.Influence of Additional Tensile Force on Springback of Tube under Rotary Draw Bending[J].Journal of Materials Engineering and Performance，2012，21(11):2316 －2322.

[6]陈吉生，鄂大辛，张敬文.材料模型对1Cr18Ni9Ti管材拉伸有限元仿真的影响[J].精密成形工程，2012，4(4)，10 －12，80.