考虑径向加质的固体火箭发动机内流场整体稳定性分析①

杨尚荣，刘佩进，魏少娟，魏祥庚

(西北工业大学燃烧、热结构与内流场重点实验室，西安 710072)

0 引言

大型分段固体火箭发动机中的压强振荡主要是涡脱落现象引起的［1］。理论上，CFD(例如LES)可完整地模拟涡脱落与声场的耦合过程，预示燃烧室内压力振荡的频率和幅值［2］。但实际预估时，由于发动机几何尺寸较大，工作时间又很长(大于100 s)，对每一时刻的工作状态进行数值模拟计算是不现实的，因此有必要从稳定性理论角度出发，对涡脱落的机理进行研究。

缩比发动机［3］和冷流实验［4－5］都证明单纯表面涡脱落也可引起发动机内的压强振荡，并且其振荡幅值强于由障碍涡脱落导致的振荡幅值［6］。与由剪切不稳定产生的障碍涡脱落相比，表面涡脱落被认为是由固体推进剂燃烧生成的径向加质流的“本质不稳定”决定的［7］。相似的是，它们都可以用流动不稳定性理论来研究并获得不稳定特征以及演化规律。

Casalis等［7］利用局部非平行方法讨论了平面径向加质流的不稳定模式，发现平均流的横向分量对稳定性结果有很大的影响。计算结果表明分别用主变量和势函数表示的扰动方程得到的结果会有差异［8－9］，说明局部非平行方法是不一致的。文献［10］同样利用局部方法研究了圆柱构型的径向加质流不稳定特征，但其与实验结果的差距较大，认为该方法不太适合于圆柱构型的研究［11］。Chedevergne［11－13］采用了整体稳定性方法重新讨论了该问题，解决了局部方法带来的不一致问题，得到的特征值虚部即时间增长率皆为负值，即它们是时间稳定的。因此，其认为实验中出现的表面不稳定现象应该是由某些外在的噪声激发的。

本文使用更合理的边界条件，利用整体流动稳定性方法研究了圆柱构型的径向加质流整体不稳定特征，来解释上述理论与实验的差异，以加深对固体火箭发动机内由于表面涡脱落引起的不稳定现象的理解，并为分段发动机稳定性分析提供一种快速、有效的手段。

1 控制方程

采用不可压缩粘性流体N－S方程，在轴对称坐标系下(图 1)，无量纲速度向量 U=(Ur，Uθ，Uz)和压强 p满足［11］:

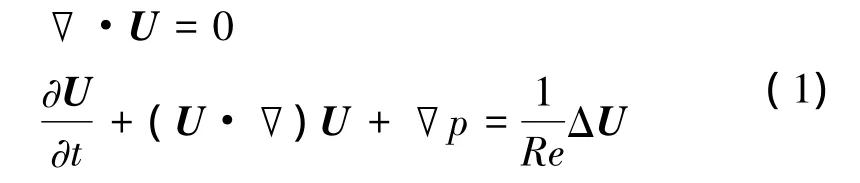
其中，无量纲参考量为半径R(长度)、径向加质速度Vinj(速度分量)、R/Vinj(时间)、ρV2inj(压强)，密度 ρ假定为常数，雷诺数Re=VinjR/ν依赖于径向加质速度和半径，ν为运动粘性系数。

把瞬态解分解为稳态和扰动部分的和，U=Ub+u，p=pb+p，带入方程(1)，并消去 Ub，pb满足的稳态方程，可以得到扰动方程:

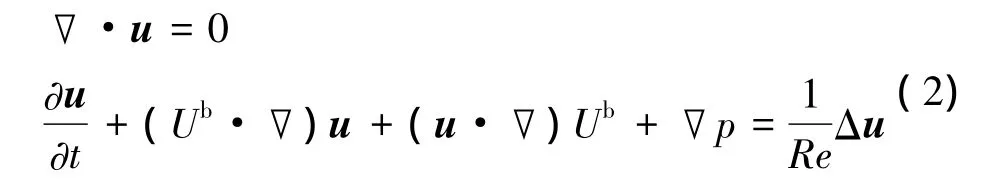
流动稳定性分析便是在一定的边界条件下去求解上述方程(2)，得到扰动量u和p随时间的变化(特征值)及其在空间的分布(特征函数)。方程(2)中用到了稳态流场解Ub，需要提前计算。在无粘且前端无滑移条件下，Taylor和Culick分别独立地得到了方程(1)的稳态精确解［10］，数值计算表明，在 Re＞100时，精确解与数值解相当接近［7］。因此，本文采用该精确解进行稳定性计算，如下式所示:

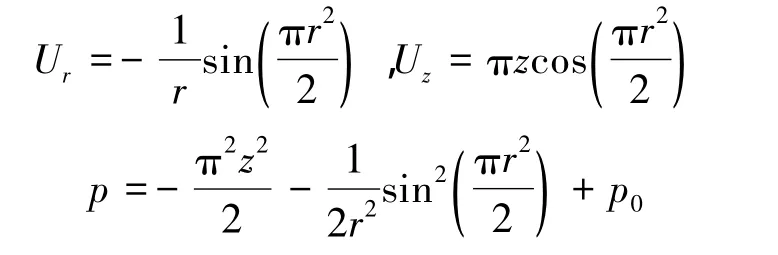
2 整体稳定性分析

局部方法假定扰动量 q=(p，ur，uθ，uz)为如下形式:

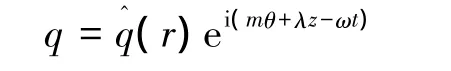
整体稳定性分析则把扰动量 q=(p，ur，uθ，uz)写成如下的形式:

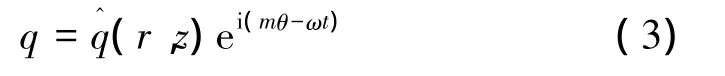
式中 m为整数，代表角波数;ω为复数，实部ωr代表无量纲角频率，ωi代表时间增长率。

本文只讨论轴对称模态，此时m=0，uθ=0。把式(3)代入微分方程(2)，便得到了如下的广义特征值问题:

其中，A与B为3×3矩阵，各分量在柱坐标下的表达式为

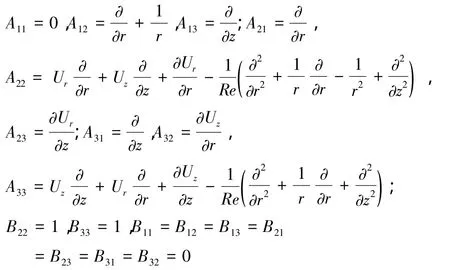
求解特征值(4)需要合适的边界条件，速度扰动在头部和壁面应为0，r=0处设为轴对称条件。文献［11］在尝试了多种出口边界条件之后，认为出口处取插值条件较为理想，但后来发现其结果与 DNS［14－15］结果相差较大。在研究后向台阶的瞬态增长时，Blackburn［16］认为出流边界处取法向应力为0更为合理，本文出口处便采用了该种边值条件。计算所用边界条件总结如下:

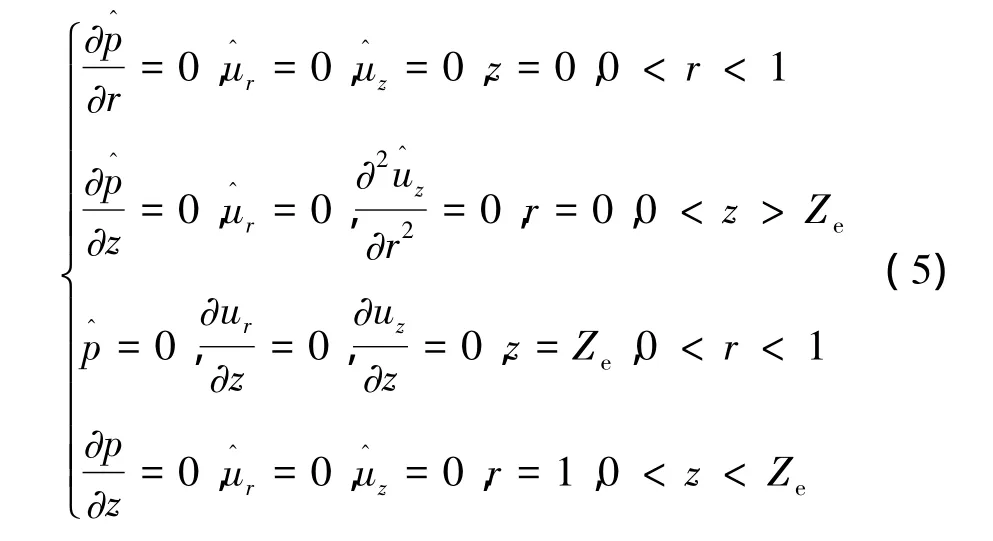
3 结果分析

利用谱配置方法［17－18］和边值条件(5)求解特征值问题(4)，径向×轴向网格量为20×50。数值计算了Re=2 100时的特征模态，如图2所示。可看到长径比L/R分别为10和8时，两者特征值的实部，即无量纲角频率ωr相差不大，但前者的虚部，即能量时间增长率ωi明显大于后者，并且有些越过了临界值0，由稳定模态变成了不稳定模态。这证明了文献［15］中的猜测，即当长径比大到一定程度后，ωi将为正值，时间特征由衰减变为增长。已有的冷流实验［19－21］中长径比都大于10，且都出现了表面不稳定现象，这与上述的理论结果一致，证明了外部噪声不是产生表面不稳定的必要条件。

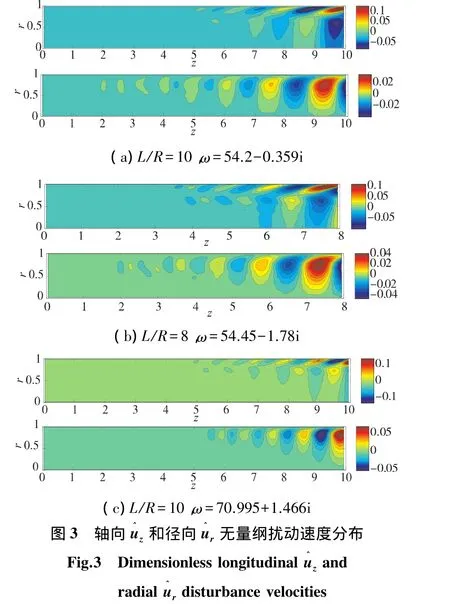
不同长径比及特征值的扰动速度的分布见图3。从图3(a)看出，无论轴向扰动速度(上图)，还是径向扰动速度(下图)，其沿轴向都是逐渐增大的，且向内部扩张。同一径向位置，接近壁面的地方扰动达到最大，这与文献［19］中实验结果一致。径向扰动速度在z=2的地方就已存在，其幅值比轴向扰动速度幅值小了一个数量级。图3(b)为L/R=8时扰动速度的分布，该特征值与图3(a)中的特征值有着相近的实部，但其虚部要小一些。两图中的扰动速度分布很相似，幅值也相差不大，只不过L/R=8时扰动存在的位置更靠前。与图3(a)相比，图3(c)不稳定波的波长较短，径向扰动速度出现位置明显靠后。

4 实验验证

为了与实验结果比较，需把理论求解得到的一系列特征值ωM(其实部为角频率)，量纲化为

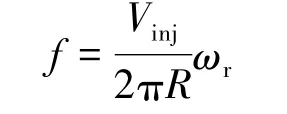
文献［19］利用径向加质轴对称冷流实验器对固体发动机燃烧室内的气动声学做了深入的研究。实验器半径 R=30 mm，空气径向加质速度 Vinj可在 0.8 ～2.0 m/s之间变化。在加质边界附近测得的不稳定频率随径向加质速度的变化如图4所示，图4(a)为径向加质速度递增时的扰动速度频率，图4(b)为径向加质速度递减时的扰动速度频率。从图4看到，理论和实验吻合得很好。实验中的不稳定频率有数条轨迹，但它们都在理论解的范围内。在径向加质速度大于1.7 m/s时，实验结果开始偏离理论值，应归因于实验中使用的供气系统，压力过高时，其与径向加质速度的线性关系可能已不再适合。

Dunlap［20］设计的冷流实验器半径R=50 mm，氮气径向加质马赫数见表1，实验中气体温度在257～286 K之间，本文计算中选取了温度的两边界值，取上界时，偏差在2%以内，取下界时，偏差在6%内。

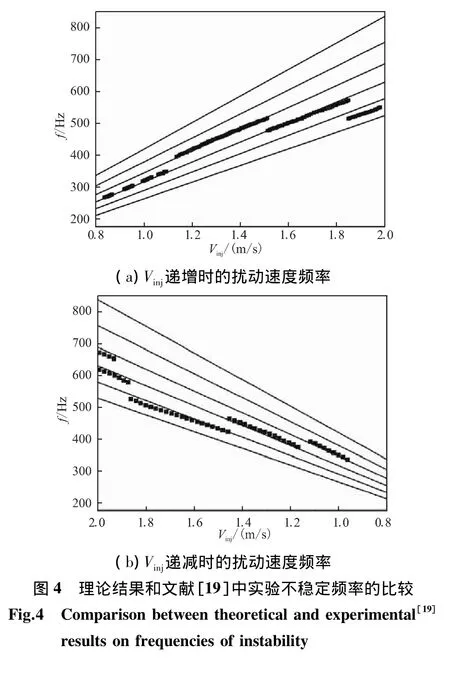
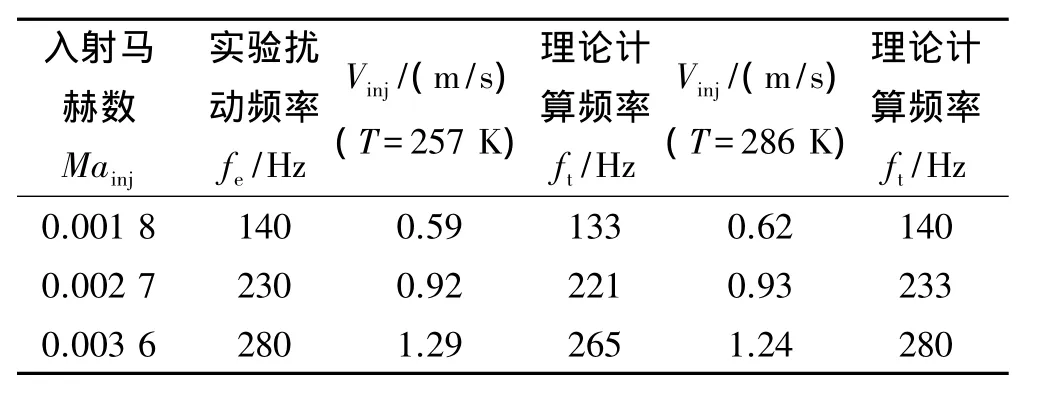
表1 理论结果和文献［20］中实验不稳定频率的比较Table 1 Comparison between theoretical and experimental results［20］ on frequencies of instability

VKI流体力学研究中心Anthoine［21］设计了Ariane 5 MPS的1/30缩比冷流实验器来研究表面涡脱落引起的压力振荡。实验器 L=0.63 m，D=0.076 m，喷管入口处马赫数Ma0=0.09，按下式计算得到径向加质速度［21］:

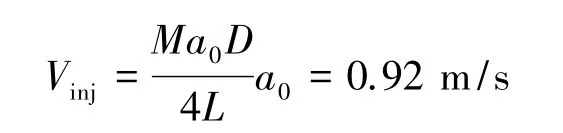
实验中在L/R=10处测得的不稳定频率为270 Hz和350 Hz，本文理论计算结果为273 Hz和337 Hz，偏差在4%以内。

5 结论

(1)圆柱形径向加质流的整体不稳定分析发现特征谱是离散的，且随着长径比的增加，特征值的虚部明显变大，而其实部变化不大，在L/R=10时虚部从时间稳定变为不稳定。

(2)特征函数表明，轴向和径向扰动速度沿轴向逐渐增大，且向内部扩张，同一径向位置，接近壁面的地方扰动达到最大。

(3)理论结果准确地估计了实验中出现的不稳定频率，证明流动稳定性方法可以解释固体火箭发动机内的表面不稳定现象，也可以对发动机内的表面涡脱落现象和流动稳定性进行预估。

［1］Dotson K W，Koshigoe S，Pace K K.Vortex shedding in a large solid rocket motor without inhibitors at the segment interfaces［J］.Journal of Propulsion and Power，1997，13(2).

［2］Zhang Q，Wei Z J，Su W X，et al，Theoretical modeling and numerical study for thrust oscillation characteristics in solid rocket motors［J］.Journal of Propulsion and Power，2012，28(2).

［3］Lupoglazoff N，Vuillot F.Parietal vortex shedding as a cause of instability for long solid propellant motors:numerical simulations and comparisons with firing tests［R］.AIAA 96－0761.

［4］Avalon G，Casalis G，Griffond J.Flow instabilities and acoustic resonance of channels with wall injection［R］.AIAA 98－3218.

［5］Avalon G，Ugurtas B，Grisch F，et al，Numerical computations and visualization tests of the flow inside a cold gas simulation with characterization of a parietal vortex shedding［R］.AIAA 2000－3387.

［6］Anthoine J，Lema M R.Passive control of pressure oscillations in solid rocket motors:cold－flow experiments［J］.Journal of Propulsion and Power，2009，25(3).

［7］Casalis G，Avalon G，Pineau J P.Spatial instability of planar channel flow with fluid injection through porous walls［J］.Physics of Fluids，1998，10(10).

［8］Griffond J，Casalis G.On the dependence on the formulation of some nonparallel stability approaches applied to the taylor flow［J］.Physics of Fluids，2000，12(2).

［9］Griffond J，Casalis G.On the nonparallel stability of the injection induced two－dimensional taylor flow［J］.Physics of Fluids，2001，13(6).

［10］Griffond J，Casalis G，Pineau J P.Spatial instability of flow in a semi－infinite cylinder with fluid injection through its porous walls［J］.Eur.J.Mech.B－Fluids，2000，19.

［11］Chedevergne F，Casalis G，Feraille T.Biglobal linear stability analysis of the flow induced by wall injection［J］.Physics of Fluids，2006，18.

［12］Chedevergne F，Casalis G.Thrust oscillations in reduced scale solid rocket motors，part Ⅱ:a new theoretical approach［R］.AIAA 2005－4000.

［13］Chedevergne F，Casalis G.Detailed analysis of the thrust oscillations in reduced scale solid rocket motors［R］.AIAA 2006－4424.

［14］Casalis G，Boyer G，Radenac E.Some recent advances in the instabilities occurring in long solid rocket motors［R］.AIAA 2011－5642.

［15］Chedevergne F，Casalis G，Majdalani J.DNS investigation of the taylor－culick flow stability［R］.AIAA 2007－5796.

［16］Blackburn H M，Barkley D，Sherwin S J.Convective instability and transient growth in flow over a backward－facing step［J］.Journal of Fluid Mechanics，2008:603.

［17］Weideman J A C，Reddy S C.A matlab differentiation matrix suite［J］.ACM Trans.Math.Softw.，2000，26(4).

［18］Trefethen L N.Spectral methods in matlab［J］.Society for Industrial and Applied Mathematics，Philadelphia，2000.

［19］Cerqueira S，Avalon G，Feyel F.An experimental investigation of fluid－structure interaction inside solid propellant rocket motors［R］.AIAA 2009－5427.

［20］Dunlap R，Blackner A，Waugh R，et al.Internal flow field studies in a simulated cylindrical port rocket chamber［J］.Journal of Propulsion and Power，1990，6(6).

［21］Anthoine J.Experimental and numerical study of aeroacoustic phenomena in large solid propellant motors［D］.PhD thesis，Universite libre，Bruxelles，October，2000.