地铁车辆车轮磨耗仿真研究*

丁军君 黄运华 李 芾

(1.西南交通大学机械工程学院，610031，成都;2.西南交通大学土木工程博士后流动站，610031，成都∥第一作者，讲师)

车轮磨耗是影响地铁运输安全性和经济性的重要因素。车轮磨耗后，车辆平稳性变差，临界速度下降。同时，由于车轮镟修等原因将造成运营成本增加。目前，国内对地铁车辆车轮磨耗的研究集中在车轮踏面的异常磨耗上［1－5］;而车轮磨耗仿真研究始于上世纪90年代，且主要集中在重载货车和高速列车上［6－7］，尚未应用于地铁车辆。本文对地铁车辆的车轮磨耗行为进行研究，通过建立地铁车辆系统动力学模型，结合轮轨滚动接触理论和车轮磨耗模型，对车轮磨耗过程进行仿真，得到车轮磨耗后的踏面形状和磨耗分布，为地铁车辆车轮磨耗问题的研究提供一定的参考依据。

1 车轮踏面磨耗模型

Braghin在BU 300全尺寸试验台上对轮轨磨耗进行试验，并根据试验结果建立了车轮踏面磨耗数值模型［8］。在该模型中，将接触斑分为黏着区Aa和滑动区As，而磨耗只发生在滑动区内，如图1所示。

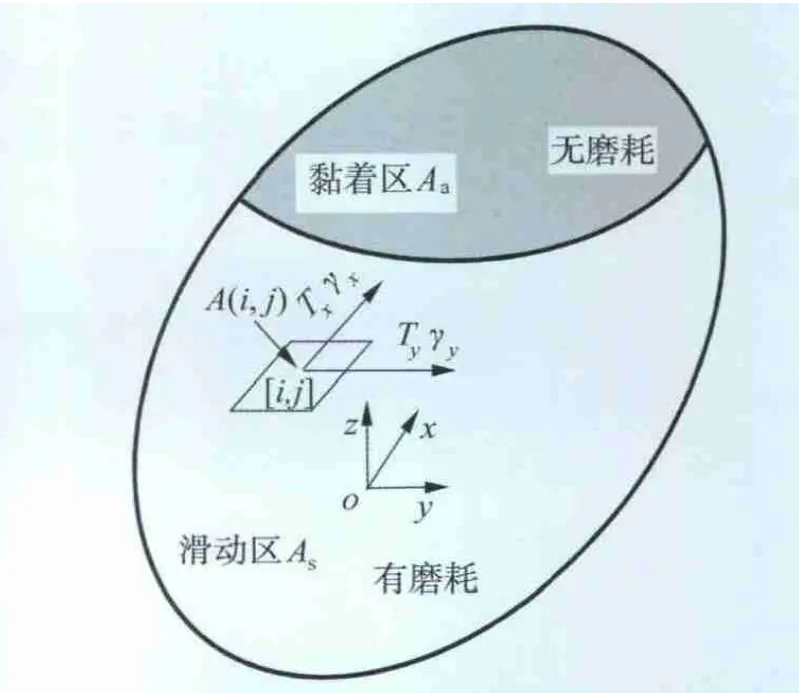
图1 接触斑内黏滑区分布示意图

接触斑内单元格(i，j)处的磨耗深度为［8］:

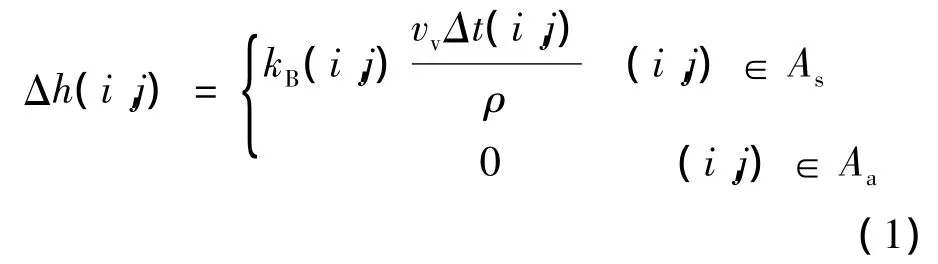
式中:

Δh——磨耗深度;

vv——车辆运行速度;

Δt——车轮通过该单元格的时间;

ρ——车轮材料密度;

kB——磨耗率。

kB与 T(i，j)·γ(i，j)/A(i，j)的值有关(见表1)。其中 T(i，j)为单元格(i，j)内的蠕滑力，γ(i，j)为蠕滑率，A(i，j)为单元格面积。

表1 Braghin模型磨耗区分布与磨耗率

2 轮轨滚动接触理论

2.1 FASTSIM 算法

在线性理论的基础上，Kalker发展了简化理论，即FASTSIM算法。在该算法中，假设材料表面弹性位移u与面力p和柔度系数L相关［9－10］:

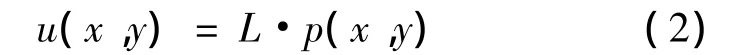
接触斑内稳态情况下的一般性滑动方程为［9］:

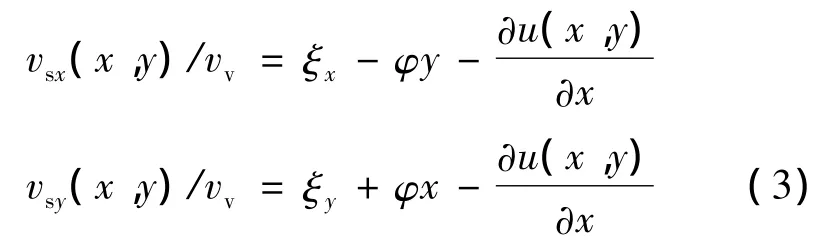
式中:

vsx，vsy——分别x和y方向的滑动速度;

ξx，ξy，φ——分别为纵向、横向和自旋的蠕滑率。

对式(3)进行无量纲处理后，将椭圆接触斑转化为图2所示的单位圆接触斑。根据接触斑内任一点位置处的刚性滑动量，对接触斑内任一平行于x'轴且宽为dy'的长方形带中的任一点x'1=(x'0－h)到x'0进行积分，得到该点处的切向应力，然后根据法向接触应力和摩擦系数确定该点的黏滑状态。

2.2 接触斑内滑动速度比较

通常情况下，刚性滑动速度远大于弹性滑动速度，因此在计算磨耗时忽略弹性滑动速度的影响，仅考虑刚性滑动速度［11］:

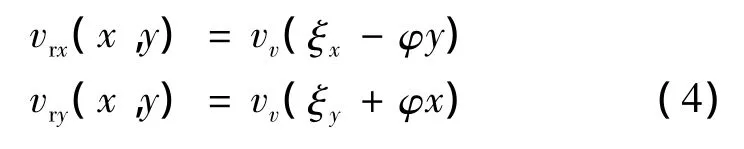
式中:

vrx，vry——分别为x和y方向的刚性滑动速度。

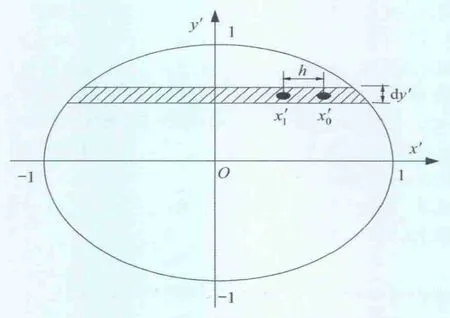
图2 转化后的单位圆示意图

当考虑弹性滑动速度时，根据式(2)和(3)，接触斑内的弹性滑动速度为:

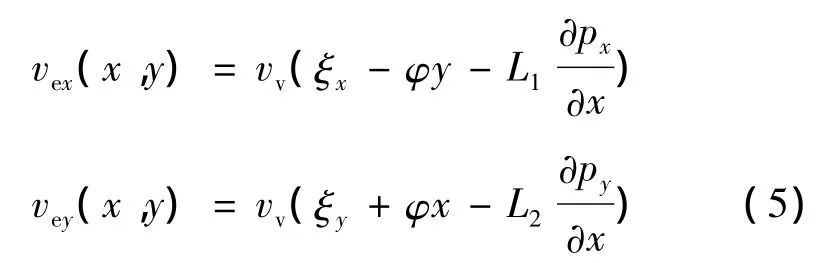
式中:

vex，vey——分别为x和y方向的弹性滑动速度;

px，py——分别为x和y方向的切向应力;

L1，L2——分别为x和y方向的柔度系数。

在部分滑动和纯滑动条件下，接触斑内y=0时的滑动速度随纵向坐标x的变化如图3所示。将其与Kalker完全理论程序CONTACT进行比较，结果表明:在部分滑动条件下，CONTACT的滑动速度介于弹性滑动速度和刚性滑动速度之间，刚性滑动速度偏小;在纯滑动条件下，弹性滑动速度与CONTACT计算结果较为吻合，刚性滑动速度相差较大。

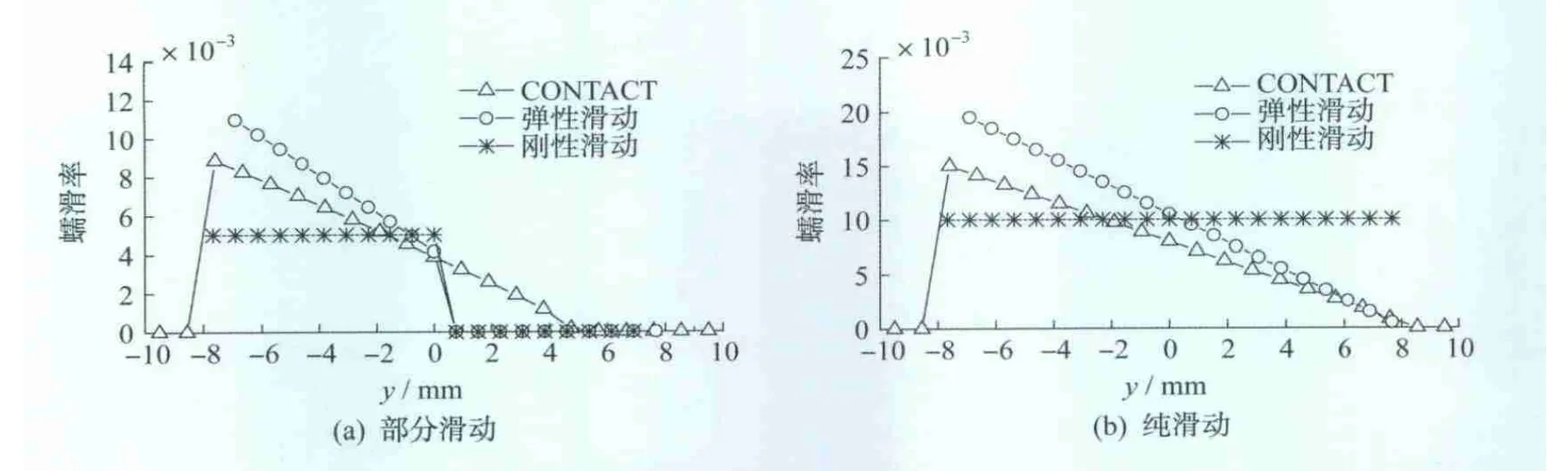
图3 接触斑内滑动速度比较

2.3 接触斑内磨耗量比较

考虑刚性和弹性滑动速度时，计算不同纵向蠕滑率和横向蠕滑率条件下接触斑内总的磨耗量，并与CONTACT计算结果进行比较，如图4所示。结果表明:CONTACT的磨耗量最大，当考虑弹性滑动速度时，其计算结果较刚性滑动更接近CONTACT计算结果。

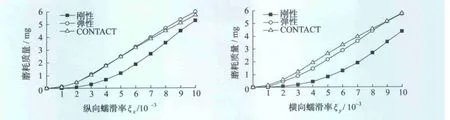
图4 接触斑内磨耗量比较

综上所述，弹性剪切变形对磨耗有较大影响，因此在车轮磨耗仿真中应用弹性滑动速度代替刚性滑动速度。

3 车轮磨耗仿真分析

根据多体动力学理论，以国产某型地铁车辆为例，在SIMPACK中建立车辆系统动力学模型。轮轨关系为LM型车轮踏面和60 kg·m－1级钢轨型面匹配，采用Kalker简化理论求解轮轨蠕滑力，同时考虑非线性悬挂力。车轮磨耗仿真过程描述为:利用车辆动力学模型、FASTSIM算法和Braghin磨耗模型，计算得到车辆运行一定距离后踏面上的磨耗深度分布;当最大磨耗深度达到0.1 mm时即对动力学模型中的车轮型面进行更新，反复进行迭代，最终得到磨耗后的车轮型面。在磨耗仿真过程中只对车轮型面进行更新，忽略钢轨磨耗后的形状对车轮磨耗的影响。

3.1 直线上车轮的磨耗仿真

车辆在直线上运行时，磨耗后的车轮型面与运行距离的关系如图5(a)所示，踏面上磨耗深度的分布如图5(b)所示。由图5可知，车辆在直线上运行时，磨耗分布在－30～35 mm范围内，磨耗主要发生在踏面上，没有发生轮缘磨耗;随着运营里程的增加，磨耗速度变慢。

3.2 曲线上车轮的磨耗仿真

车辆在半径为300 m的曲线上运行时，磨耗后的车轮型面和磨耗深度分布如图6所示。结果表明:车辆在小半径曲线上运行时，磨耗分布在－50～40 mm范围内;由于在计算中假设车辆通过左曲线和右曲线的概率相同，因此车轮踏面和轮缘同时出现磨耗，以轮缘磨耗为主，其磨耗速度远远大于直线上的磨耗速度;在－10～0 mm范围内由于接触较少故磨耗最少。

3.3 实际线路上车轮磨耗仿真

以国内某条地铁线路为例建立车辆动力学仿真所需的线路模型。该线路全长40 km，曲线半径及其对应的曲线长度如图7所示。轨道谱选用美国5级线路不平顺谱，磨耗后的车轮型面和磨耗深度分布如图8所示。结果表明:车辆在该线路上运行时，磨耗主要分布在－50～40 mm范围内;由于线路中小半径曲线较多，因此轮缘磨耗较严重，从轮缘到踏面磨耗逐渐减小;随着运营里程的增加，轮缘和踏面上的磨耗速度都变慢。图9为车轮轮缘厚度随运行里程的变化情况。可见轮缘厚度随运行里程的增加呈线性减小。

图5 直线上车轮的磨耗分布

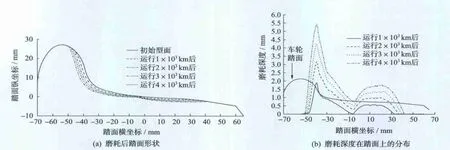
图6 曲线上车轮的磨耗分布

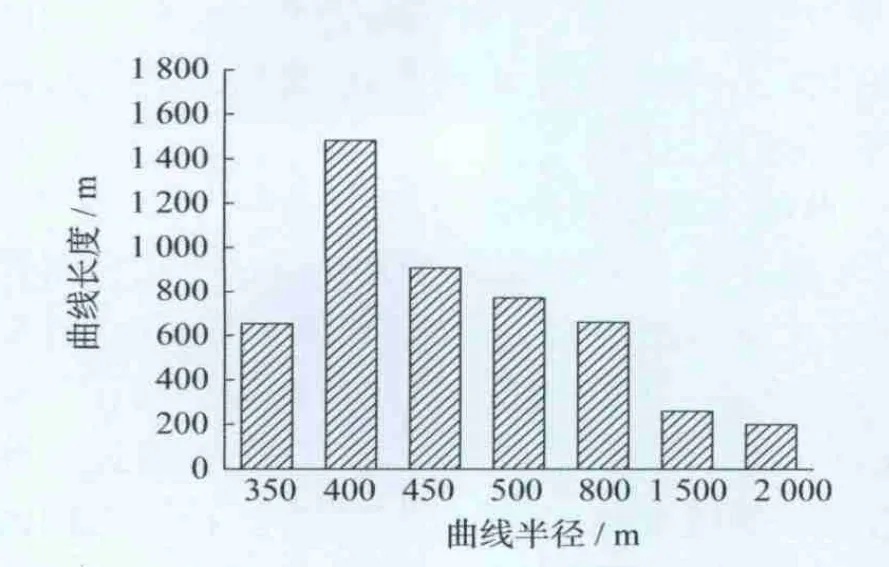
图7 某地铁线路曲线半径及长度

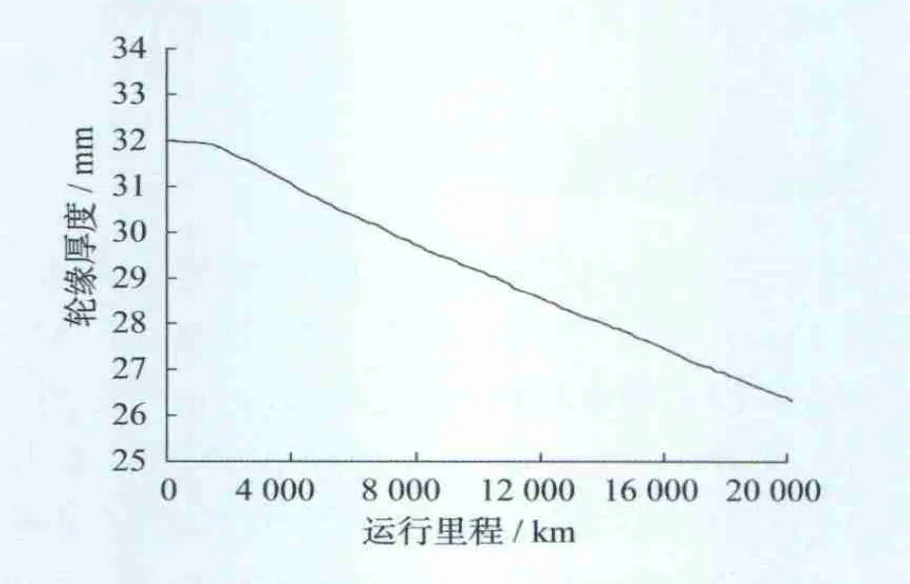
图8 轮缘厚度与运行里程的关系

4 结论

综上所述，考虑弹性滑动速度时的磨耗计算结果与CONTACT更为接近，因此在磨耗分析中应考虑弹性滑动速度。车辆在直线上运行时，磨耗分布在－30～35 mm范围内，没有轮缘磨耗发生;车辆在小半径曲线上运行时，磨耗分布在－50～40 mm范围内，车轮踏面和轮缘同时出现磨耗，以轮缘磨耗为主，其磨耗速度远大于直线上的磨耗速度;在－10～0 mm范围内由于接触较少故磨耗最少。以国内某地铁线路为例进行的车轮磨耗仿真结果表明，磨耗主要分布在－50～40mm范围内，轮缘磨耗较严重，从轮缘到踏面磨耗逐渐减小;随着运营里程的增加，轮缘和踏面上的磨耗速度都变慢，轮缘厚度随运行里程的增加线性减小。

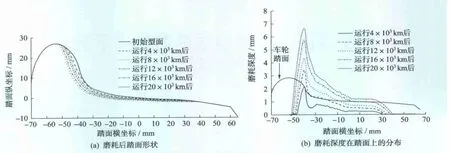
图9 实测线路上车轮的磨耗分布

［1］李洪，宗清泉，吴井冰，等.南京地铁列车车轮踏面非正常磨耗初析［J］.城市轨道交通研究，2007(7):54.

［2］方宇，穆华东，朱祺.上海地铁3号线车轮踏面异常磨耗分析［J］.机车电传动，2010(2):45.

［3］李霞，温泽峰，金学松.地铁车轮踏面异常磨耗原因分析［J］.机械工程学报，2010，46(16):60.

［4］乔青峰.地铁车辆车轮踏面异常磨耗原因初探［J］.铁道车辆，2011，49(6):28.

［5］周宇，詹刚，许玉德.城市轨道交通小半径曲线钢轨磨耗分析［J］.城市轨道交通，2011(7):42.

［6］丁军君，李芾，黄运华.重载货车车轮磨耗仿真［J］.交通运输工程学报，2011，11(4):56.

［7］罗仁，曾京，戴焕云，等.高速列车车轮磨耗预测仿真［J］.摩擦学学报，2009，29(6):551.

［8］Braghin F，Lewis R，Dwyer R S.A mathematical model to predict railway wheel profile evolution due to wear［J］.Wear，2006，261(11):1253.

［9］Kalker J J.A fast algorithm for the simplified theory of rolling contact［J］.Vehicle System Dynamics，1982，11(1):1.

［10］金学松，刘启跃.轮轨摩擦学［M］.北京:中国铁道出版社，2004.

［11］Jendel T.Prediction of wheel profile wear-comparisons with filed measurements［J］.Wear，2002(1):89.