一种降低码构造复杂度的QSTBC设计

许冰祥，彭文杰

（河海大学 计算机与信息学院，江苏 南京 211100）

随着现代数字通信技术的不断发展，相应的通信标准和产品对诸如传输质量、传输效率等移动网络传输技术的要求也越来越高，为了尽可能地增加系统容量和提高数据的传输速率，多输入多输出（MIMO）技术以其显著的传输优越性越来越被人们所关注[1]。

近年来有关MIMO多天线系统空时编码技术的研究表明，空时编码能同时利用时间和空间两维信息来构造码字，从而提高了系统的抗衰落特性；该技术还可以利用衰落信道的多径传播和发射分集以及接收分集来为用户提供高速率、高质量的数据通信。在诸多MIMO空时编码方案中，正交空时分组码（OSTBC）[2]虽然能够实现全分集特性，但是当传输天线数目超过2的时候，却达不到满速率；而准正交空时分组码（QSTBC）不仅能够达到满分集，还能实现满速率，因此得到了广泛研究。

文献[3]采用准正交空时分组码，在八发一收天线条件下，将码字映射到多维分圆格上，然后通过最大似然译码准则将信号还原，得出了采用分圆格进行码字设计的优越性，即：满分集很容易保证；分集上限直接取决于多维格点的最小欧氏距离（MED）；能达到更高的分集增益。但是，该文献中原始的八发一收准正交空时分组码的编码矩阵过于繁琐，并不利于系统的分析与设计。为了简化这一码字矩阵，本文依据分圆格思想设计了一种基于分圆格的四发四收准正交空时分组码，新设计的四发四收准正交空时码不仅具有良好的分集增益和编码增益，在误码率、信道容量和中断概率及算法复杂度方面皆具有较原设计较显著的优越性。

1 系统模型

为研究方便，文中仅考虑准静态平稳衰落信道中的传输情形。假设有一采用准正交空时编码技术的nT×nRMIMO系统，其中nT为发射天线数，nR为接收天线数，信号接收模型为

其中，Y是一个T×nR的接收矩阵，ρ是每一个接收天线的信噪比，C是码字矩阵，H是nT×nR信道矩阵，N是 T×nR噪声矩阵，H和N中的元素独立同分布，并且都服从于复高斯分布，即CN（0，1）分布。此处的T是每组码中所包含的信号数。

本设计中的码字矩阵依据Alamouti准则设为[4]：

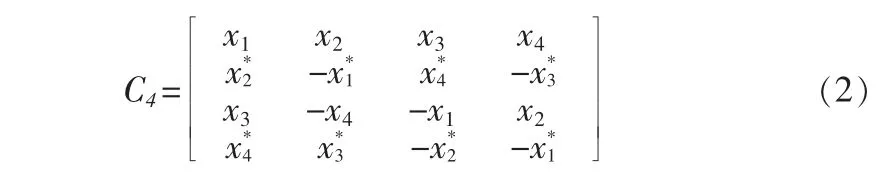
码字矩阵C4的能量为

其中，E表示期望，‖‖F表示F范数，式（3）将C4归一化。

式（1）经过匹配滤波和噪声白化后[4]得到的等效接收信号模型为：

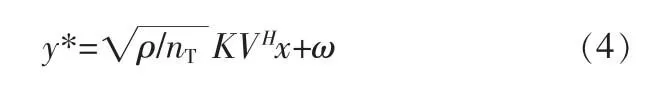
y*是接收向量，K是一个实对角阵，x为发射信号，其中的每个元素对应一个单输入单输出信道，ω是一个满足复高斯分布的噪声矩阵，V是一个经奇异值分解后得到的酉矩阵。

2 基于分圆格的四发四收准正交空时分组码设计

在介绍具体的基于分圆格准正交空时分组码设计之前，首先根据古典代数理论，介绍2个有关分圆格的基本定义[5]。

定义一：一个整数环Z[ζm]上的四维复分圆格为：

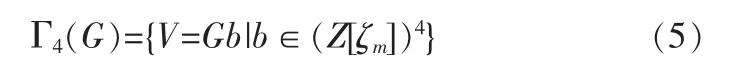
其中，V=[V1V2V3V4]T即二维复分圆格的格点，b=[b1b2b3b4]T，G 是 4×4 复生成矩阵，m 是正整数；Z[ζm]={z|z=z1+z2ζm，ζm=e2πj/m，z1，z2∈ωZ}，其中，ωZ 是一个有范围的整数集，ω 是一个正比例因数。 事实上，ω 是整数环 Z[ζm]的单位长度；（Z[ζm]）4是四维列向量的集合，向量中的元素属于整数环Z[ζm]。

定义二：四维分圆格 Γ4（G）的最小乘积距离（MPD）由下式表示

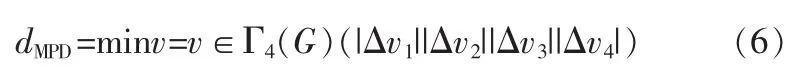
其中 v，v′∈Γ4（G），Δv=v-v′=[Δv1Δv2Δv3Δv4]T并且 v≠v′。 标准化 dMPD=（dMPD）1/4。

定义发射信号向量s=[s1s2s3s4]T，并令x=V4s。在该传输系统中，将发送符号调制为四维分圆格中的格点。假如ΔC4=C4-C′4是2个不同码字C4和C4的差矩阵，而C4和 C4则分别对应于两不同向量或者说格点 s和 s′。 令 Δs=s-s′=[Δs1Δs2Δs3Δs4]T。

结合文献[3]的内容，得到分集增益为：

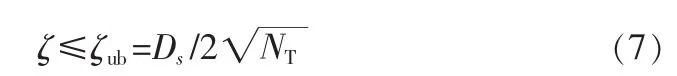
随后将选取所使用的格，此处采用最优的爱因斯坦分圆格[6]：

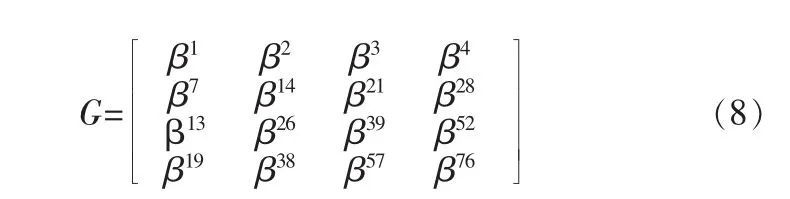
其中，β=ejπ/15，Γ4（G）基于整数环 Z[ζ6][6]。

根据式（6）和式（7），可以得到[3]：

其中，ω在文中第2节的定义一中已经定义。

接下来进行格压缩过程，即将定义一中的ω最大化。令M=4来表示分圆格Γ4（G）的维数，R为每个信道周期的比特吞吐量（bpcu），令其值为2。再接下来的问题就是如何选取L=2RM=256个格点作为信号集合来获取最大欧氏距离，此过程在文献[3]中有详细理论介绍。文中通过分析选取Θ={-2，-1，0，1}⊂z，再根据上述过程进行分析，用 MATLAB给出仿真结果。通过计算我们得到四维分圆格能达到的最大分集上界ε为 0.408 3。

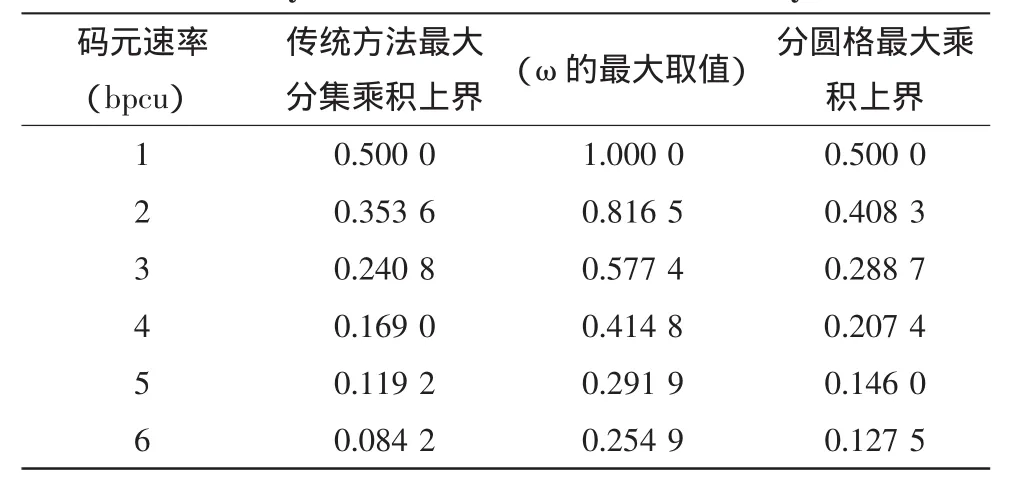
表1 四发天线系统中传统方法与格压缩理论获得的分集乘积上界比较Tab.1 Comparison of the upper bound of diversity product between the traditional method and the lattice compression theory obtained by four transmit antennas antenna system

表1给出了发射天线数为4时，采用文中分析的经典格压缩理论获得最大分集乘积上界与传统方法获得的分集乘积上界相比较的情况。可以看出，在码元速率大于1之后，利用格压缩理论能得到比传统方法获得更大的乘积上界，提升了系统的编码增益性能。当码元速率高于4之后，文献[3]中所取256个格点组成的环不够用，增大可选格点的范围，即增加Θ的取值范围，从而使其达到所需分析的最小格点数。当码元速率高于4时，根据表1，格压缩理论仍然适用，因此，在4发射天线的情况下，基于分圆格基础的准正交空时分组码比原始的复星座空间中的准正交空时分组码有更大的分集乘积上界。

3 四发四收准正交空时分组码优越性

基于分圆格的传输方式具有全分集的特性，因此可以推出4×4空时分组码的分集增益为16，优于8×1空时分组码的分集增益8。本节主要针对基于分圆格技术的准正交空时编码系统的误码率和中断概率进行分析。

首先对文中研究的基于分圆格的4发4收准正交空时编码同文献[3]中提出的8发1收准正交空时码在误码率方面进行性能比较：

我们选取本文第1节介绍的信道模型，并且信道状态信息（CSI）在接收端是已知的，但是在发送端是未知的。本文在瑞利衰落信道下，通过蒙特卡洛仿真，在100万次条件下得到图1所示。

如图1所示，在同等信噪比的条件下，4发4收方案的误码率显然比8发1收方案的小；当信噪比不断增大的时候，两条线之间的距离明显增大。因此我们可以推出：信噪比一定时，本文所研究的4×4基于分圆格准正交空时编码方案的误码率明显低于文献[3]的原始8×1编码设计实例。因此本文研究的方案能更稳定、更高效地传输数据信息。

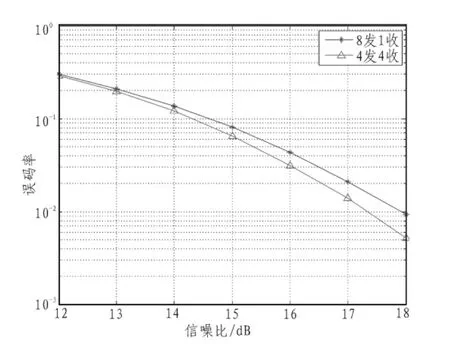
图1 4×4QSTBC和8×1QSTBC误码率比较Fig.1 Comparison of code error rate between 4×4 QSTBC and 8×1 QSTBC

中断概率是指系统瞬时信道容量比系统传输速率小的概率，它反映了系统无差错传输性能，是系统性能的重要考核指标。在发射天线数为，接收天线数为的准静态Rayleigh衰落MIMO信道系统中，其若接收端有良好的信道估计，且发射端在无信道状态信息（CSI）的情况下：

准正交空时分组码的信道容量公式为[7]：

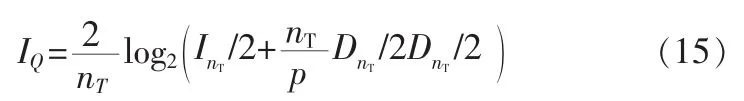
准正交空时分组码能达到的中断概率Pout定义为信道容量IQ小于某一特定传输速率R的概率：

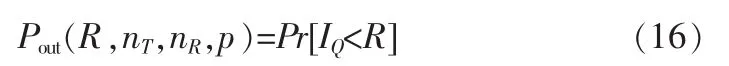
中断概率的下界公式为[7]：

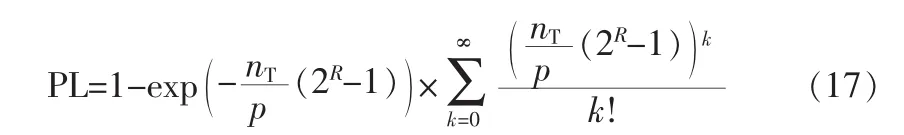
中断概率的上界估算为[7]：

图2中，加“Δ”的曲线表示4×4准正交空时分组码的信道容量曲线，标记“*”的曲线表示8×1准正交空时码的信道容量曲线。从图中看出，10%中断概率的情况下，4×4准正交空时分组码信道容量大于8×1准正交空时分组码。观察曲线的斜率可以推出其传输速率会随着SNR的增大，与8×1准正交空时分组码传输速率之间的间隔越来越大，或者说本文的4×4传输方案比文献[3]8×1方案有更好的信道容量。根据图3，在发射天线数为4的情况下，4接收天线的信道容量比小于4接收天线时的信道容量要大，适合数据传输，且4接收天线的天线阵列安排并不是很复杂，可见4发4收系统能取得较好的信道容量。

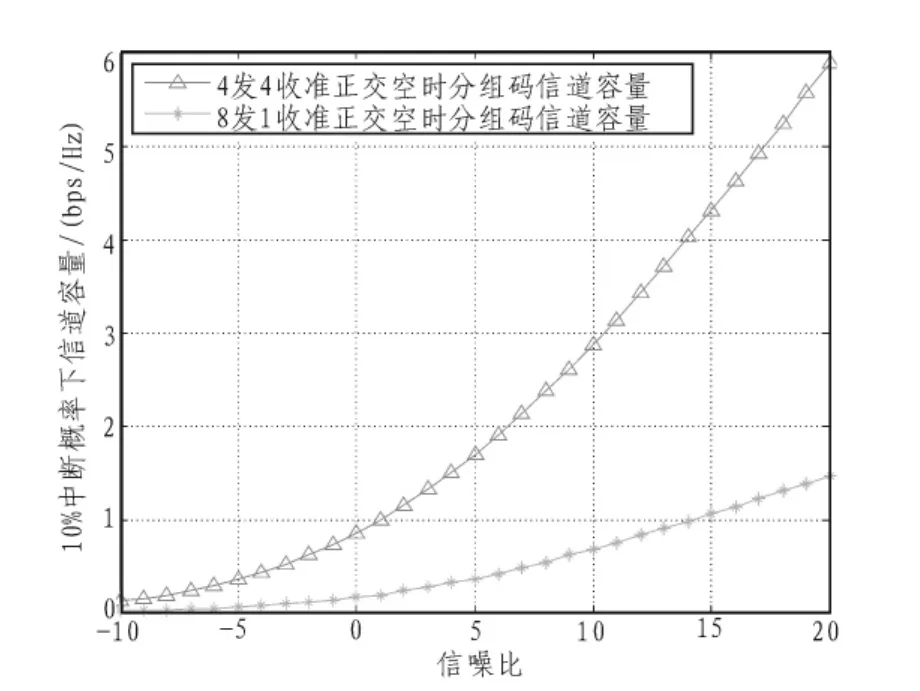
图2 4×4QSTBC和8×1QSTBC信道容量比较Fig.2 Comparison of channel capacity between 4×4 QSTBC and 8×1 QSTBC

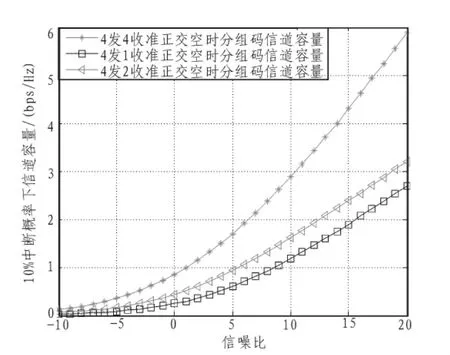
图3 10%中断概率下发射天线数为4的准正交空时分组编码信道容量比较Fig.3 Comparison of channel capacity among 4 transmit antenna with QSTBC in outage probability of 10%

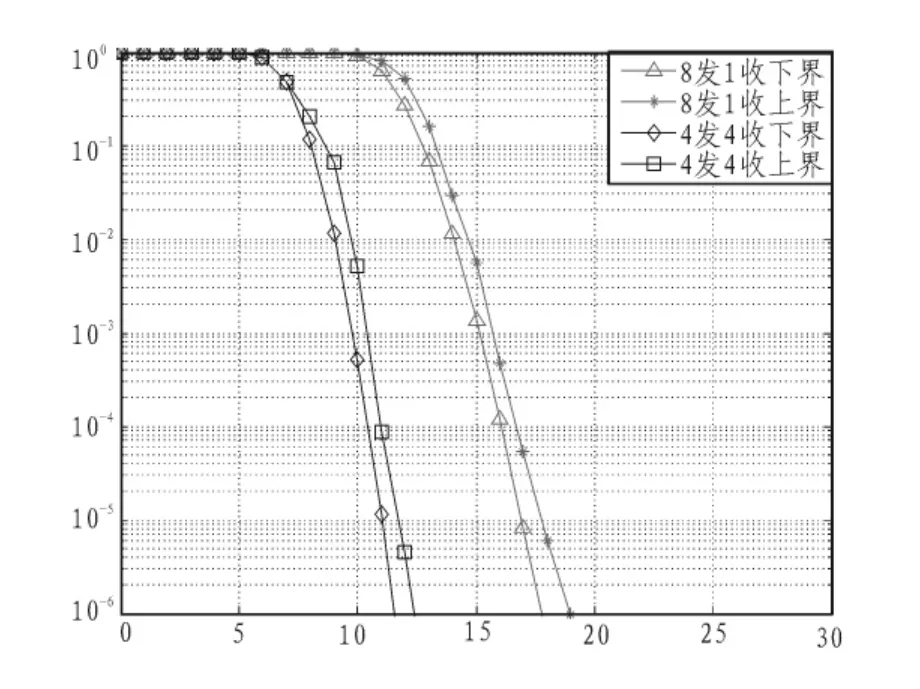
图4 本文方案与原始设计实例中断概率比较Fig.4 Comparison of outage probability between this paper program and original design example

图4则为本文4×4设计方案与文献[3]原始8×1设计实例中断概率仿真比较结果，根据图4的仿真曲线可以看出，当信噪比一定时，本文研究方案的中断概率始终低于原始设计实例。因此本文的方案能更稳定、更高效地传输数据信息。

由于在码字矩阵设计方面，本文选用的是4×4分圆格码字矩阵，由于它的传输只需要4个时隙，对信道稳定性要求比较低，而文献[3]中8×8码字矩阵的传输需要8个时隙，对信道的稳定性要求较高。尤其在译码方面，原始的8×1方案需对分为2个独立4×4的信道矩阵分别进行奇异值，而新方案只需一次奇异值分解，故计算复杂度可降一半。另外本文采用的是4接收天线，相比文献[3]中的1接收天线，我们可以先通过最大比合并（MRC）以提高信噪比，然后再译码就可以提高译码准确度。综上所述，本文研究的四发四收方案不论在计算复杂度、还是在系统误码率以及信道容量和中断概率方面都优于原始设计实例，因而能更高效更稳定地传输数据。

4 结 论

文中研究了一种降低编码矩阵构造复杂度的简化型四发四收准正交空时分组码设计方案，研究结果表明，该简化设计方案不仅可以比未采用格压缩理论的四发四收方案获得更大的分集乘积上界，而且与已有文献中的八发一收设计实例相比，在误码率、信道容量和中断概率及算法复杂度方面皆显示出其优越性。

[1]王超，廖桂生，张林让，等.微小区环境下MIMO系统相关性的测量分析[J].西安电子科技大学学报，2003，30（5）:634-639.

WANG Chao，LIAO Gui-sheng，ZHANG Lin，et al.Measurement of MIMO system in the cell environment[J].Journal of Xidian University，2003，30（5）:634-639.

[2]Tarokh V，Jafarkhani H，Calderbank A R.Space-time block codesfrom orthogonaldesigns[J].IEEE Trans.Inform.Theory，1999，45（7）:1456-1466.

[3]LIU Wei，Sellathurai，WEI Ji-bo，et al.A cyclotomic lattice based quasi-orthogonal STBC for eight transmit antennas[J].IEEE Signal Processing Letters，2010，17（4）:394-397.

[4]Sezgin A，Oechtering T J.Complete characterization of the equivalent MIMO channel for quasi-orthogonal space-time codes[J].IEEE Trans.Inform.Theory，2008，54（7）:3315-3327.

[5]Conway J H，Sloane N J A.Sphere packing， lattices and groups[M].New York:Springer-Verlag，1998.

[6]WANG Gen-yuan，LIAO Hui-yong，WANG Hai-quan，et al.Systematic and optimal cyclotomic lattices and diagonal space-time block codes designs[J].IEEE Trans.Inform.Theory，2004，50（12）:3348-3360.

[7]Sezgin A，Oechtering T J.Comeplete characterization of the equivalent MIMO channel for quasi-orthogonal space-time codes[J].IEEE Trans.Inform.Theory， 2008，54（7）:3315-3327.