非均匀采样的频谱研究

李 杰，赵红东，苏 周

（河北工业大学 天津 300401）

信号采样问题是信号处理中的一个基本问题[2]，利用计算机来处理连续时间信号，首要的问题就是要将时间和幅度都连续的模拟信号转换成离散信号，得到数字信号。模拟信号要数字化，就是对其进行离散化处理。采样就是实现将连续的模拟信号在时间上离散化的过程。从采样时间的间隔不同的角度上可以将采样分成两种——均匀采样和非均匀采样[3]。非均匀采样是相对于均匀采样提出的一种采样方法，非均匀采样有时也会被称为随机采样。理想均匀采样的采样时间间隔完全相等，而非均匀采样的采样时间间隔是不确定的[4]。现实中经过采样得到的真实数据，采样时间间隔往往是非均匀的[5]。

1 非均匀离散傅里叶变换

假设 x（t）是有限带通信号，x（n）和 x（tn）其中（n=1，2，3，…，N）分别表示均匀采样和非均匀采样信号，Xs（f）为连续信号 x（t）的傅里叶变换结果，T为采样的时间间隔，N为总的采样点数，NT为总的采样时间，连续时间的傅里叶变换为：

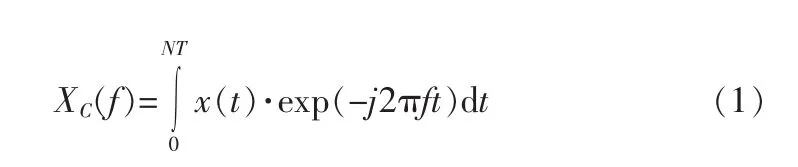
均匀采样信号的离散傅里叶变换就是将式（1）的积分换成求和累加的形式，由于均匀采样情况下采样时间间隔相等[7]，也就是每个采样时间段的宽度都相同，均匀采样信号的离散傅里叶的数学表达式为：

类似的可以得到非均匀采样的离散傅里叶变换的数学表达式为：

非均匀采样信号的傅里叶变换和均匀采样信号的傅里叶变换的主要区别在于积分时间上的不同[8]。

2 非均匀采样的频谱分析

文中将利用Matlab对式（3）进行验证，并对非均匀采样信号的数字频谱进行分析研究。设置一个简单的非均匀时间函数，将采样时间设置成非线性的关系，设置采样点总数N=1 024，设置采样时间函数的数学表达式为：

从式 （4）可以知道到采样点数和采样时间是三折线关系，t1时间段对应的采样频率为512 Hz，采样点数为256；t2时间段对应的采样频率为1 024 Hz，采样点数为256；t3时间段对应的采样频率为512 Hz，采样点数为512。

为了能够直观的观察非线性采样时间对信号频谱的检测结果，以连续的简单单正弦信号作为研究对象。简单正弦信号设置如下：

式中取f0=150 Hz。分别对正弦信号进行均匀采样和非均匀采样，非均匀采样按照式定义的非线性时间函数对正弦信号采样，并进行非均匀采样的频谱分析。频谱分析结果分别如图 1，图2所示。

其中均匀采样信号的频谱如图1所示。可以观察到图中有2个频谱成分，分别是150 Hz和 874 Hz。这2个频谱成分的相对幅值十分接近。其中，150 Hz为真实信号的频谱，874 Hz为混叠信号的频谱。

观察图 2非均匀采样信号频谱图中4个信号的频谱，分别是 150 Hz、362 Hz、662 Hz和 874 Hz。 其中 150 Hz为真实信号的频谱，幅值为1 V。由于t1时间段对应的采样频率为512 Hz，根据香农采样定理可知，512 Hz的采样频率产生的1 000 Hz以下的混叠信号分别为 512-150=362 Hz；512+150=662 Hz；2×512-150=874 Hz，由于其他的混叠信号均超过了1 000 Hz，所以图中并未显示，由此可见该采样频率产生的混叠信号分别为 372 Hz、652 Hz和884 Hz。另外，由于t1采样时间段的采样点数为256点，所以它们的频谱幅值均为0.25 V。类似的t2还有时间段对应的采样频率为1 024 Hz，该采样频率产生的混叠信号图中只能显示出一个，即1 024-140=884 Hz，由于该混叠信号和t1采样频率的884 Hz混叠信号重合，且t2采样时间段的采样点数为256点，混叠信号频谱幅值也为0.25 V，所以t1和t2采样时间的双重作用下，使得884 Hz处的频谱幅值达到0.5 V。此外，由于t3采样时间段产生的混叠信号频率均超过1 000 Hz，所以图中没有显示。

从图 1和图2之间的对比可以观察到，如果使用均匀采样结果会出现混叠信号与真实信号的频谱幅值非常接近，以至于无法准确的分辨出真实信号的频谱，所以香农采样定理要求采样频率至少为信号频率的两倍以上[9]。由于本例中均匀采样使用的采样频率为1 024 Hz，根据香农采样定理的要求可知此采样频率理论上只能够检测到512 Hz以下的信号[10]，所以图2.5中874 Hz的信号将会被排除（图中874 Hz信号是由于采样周期性延拓的结果，以下为了说明的方便会将统称为混叠信号）。所以均匀采样可以使用香农采样定理来排除混叠的频谱，从而检测得到真实的信号频谱[11]。如果使用非线性采样，由图2可以观察到，频谱图中真实信号频谱的相对幅值大于混叠信号的相对幅值，所以非线性采样可以方便的直接依据频谱的相对幅值来检测出真实信号。

图1 均匀采样频谱结果Fig.1 Uniform sampling frequency spectrum

图2 三折线非均匀采样频谱Fig.2 Non-uniform sampling frequency spectrum of Three line

从以上分析可以看出，当采样时间的非线性程度越大，混叠频谱的幅值会不断的降低。可以推想如果将采样时间设置为完全随机，那么混叠频谱的幅值将可能会下降到更低[12]。现定义采样时间函数的数学表达式为：

式中rand定义为均匀分布在（0，1）之间的随机数，由于随机数的引入，可以认为采样时间间隔完全随机，同样取N=1 024，对式简单正弦信号再次采样得到如下的频谱图3。

图3 非均匀采样频谱Fig.3 Non-uniform sampling frequency spectrum

3 结 论

由于真实信号不会随采样频率的不同而变换[13]，在所有的采样点中，所以都会含有真实信号的信息；而对于混叠信号，由于每个采样频率下的混叠信号都不相同，所以出现混叠频谱已经降低到不足真实频谱幅值的1/10，不再会影响到对真实频谱的检测。

[1]郭东亮，张铁军，戴宪华.基于非均匀采样的信号频率、幅值和相位检测[J].系统工程与电子技术，2012，32（4）:662-665.

GUO Dong-liang，ZHANG Tie-jun，DAI Xian-hua.Based on the non-uniform sampling signal frequency，amplitude and phase detection[J].Systems Engineering and Electronics，2012，32（4）:662-665.

[2]刘立祥，谢剑英，张敬辕.利用小波对非均匀采样信号进行重建[J].通信技术，2002，2（32）:7-11.

LIU Li-xiang，XIE Jian-ying，ZHANG Jing-xuan.By using wavelet to non-uniform sampling signal reconstruction[J].Communication Technology，2002，2（32）:7-11.

[3]汪安民，陈良福.基于自适应陷波的非均匀采样信号处理系统[J].计算机工程与应用，2006，5（36）:13-17.

WANG An-min，CHEN Liang-fu.Based on the adaptive notch of non-uniform sampling signal processing system[J].Computer Engineering and Application，2006，5（36）:13-17.

[4]刘民，邓丹，卿粼波，等.平稳随机信号非均匀采样的分析[J].江西农业大学学报，2005，1（2）:155-157.

LIU Min，DENG Dan，QIN Lin-bo.Non-uniform sampling analysis of stationary random signa[J].Acta Agriculturae Universitatis Jiangxiensis，2005，1（2）:155-157.

[5]张薇薇.平稳信号的非均匀采样与仿真[J].通信技术，2009，42（9）:185-189.

ZHANG Wei-wei.Non-uniform sampling and simulation of stationary signal[J].Communication Technology，2009，42（9）:185-189.

[6]高玉凯，张维.非均匀采样信号的频谱分析方法[J].电测与仪表，2009，518（46）:8-11.

GAO Yu-kai，ZHANG Wei.Spectrum analysis method of non-uniform sampling signal[J].Electrical Measurement&Instrumentation，2009，518（46）:8-11.

[7]潘晓峰，刘红星.一种新的非均匀采样规则[J].振动、测试与诊断，2003，23（1）:14-17.

PAN Xiao-feng，LIU Hong-xing.A new kind of non-uniform sampling rules[J].Journal of Vibration，Measurement&Diagnosis，2003，23（1）:14-17.

[8]王廷云，初仁欣.多路A/D非均匀采样信号的数字谱分析[J].激光与红外，2000，52（3）:32-35.

WANG Ting-yun，CHU Ren-xin.Signal digital spectrum analysis of multiple A/D non-uniform sampling[J].Laser&Infrared，2000，52（3）:32-35.

[9]陶然，王越，周思永.周期信号等效非均匀采样策略研究[J].兵工学报，1999，42（3）:49-53.

TAORan，WANGYue，ZHOU Si-yong.Periodicsignalequivalent non-uniform sampling strategy research[J].Acta Armamentarii，1999，42，（3）:49-53.

[10]刘桂英，粟时平.利用小波傅里叶变换的谐波与间谐波检测[J].高电压技术，2007，53（6）:25-29.

LIU Giu-ying，SU Shi-ping.Detection between harmonic and harmonic by wavelet Fourier transform [J].High Voltage Technique，2007，53（6）:25-29.

[11]龚黎明，公茂法，李琦.基于傅里叶和小波变换的电力系统谐波分析[J].电子质量.2010，15（10）:43-47.

GONG Li-ming，GONG Mao-fa，LI Qi.Based on Fourier and wavelet transformation of the power system harmonic analysis[J].Electronic Mass，2010，15（10）:43-47.

[12]周龙华，付青，余世杰，等.基于小波变换的谐波检测技术[J].电力系统及其自动化学报.2010，78（1）:7-11.

ZHOU Long-hua，FU Qing，YU Shi-jie.The harmonic detection technology based on the wavelet transform[J].Journal of Power System and its Automation，2010，78（1）:7-11.

[13]石芳，郑文松.脉宽调制芯片在高压发生电路中的应用[J].火箭推进，2012（1）：68-71，75.

SHI Fang，ZHENG Wen-song.Application of pulse-width modulation chip in high-voltage generating circuit[J].Journal of Rocket Propulsion，2012（1）：68-71，75.