电化学教学中的两个问题

史济斌 刘国杰

(华东理工大学化学系 上海 200237)

在原电池热力学计算中，有两个看似简单的问题，但仔细追究起来，其实并不简单，只是在电化学教学中没有引起大家的关注，致使第一个问题不知其所以然，第二个问题则错在大多数物理化学教材中的表示。

1 问题一：公式是怎样导得的？

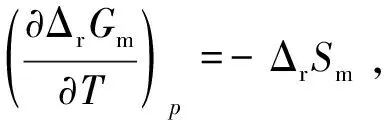
(1)

关于这个问题，并不是大家都知道其所以然。在《大学化学》杂志2011年第3期上，杨喜平等[1]提出了这个问题，我们觉得是很有意义的。但是，我们并不完全同意他们的观点，认为文中有些看法是值得商榷的。下面，谈谈我们对这个问题的理解，以供大家进一步讨论。

推导①：若有一发生化学变化的封闭系统，由K个组分和π个相构成，则系统的热力学能微变可由如下热力学基本方程描述[2]：

(2)

在恒温、恒压条件下，将热力学第一定律

dU=δQ-pdV+δW′

(3)

代入式(2)，可得:

(4)

或:

(5)

式中W′代表非体积功，等号代表可逆，不等号代表不可逆。式(5)也可表示成:

(6)

假如将化学变化设计成原电池，并使它可逆地放电做电功，则由式(6)可得:

(7)

(8)

(9)

由于原电池可逆做电功时，有：

(10)

式中z为反应电荷数，F为Faraday常量，E为原电池的电动势。故代入式(9)，可得:

(11)

由于在恒温、恒压下，系统所做的可逆电功即为Gibbs自由能减小，所以，式(10)也可以表示为:

dG=-zFEdξ

(12)

故摩尔反应Gibbs自由能为：

(13)

于是，根据热力学关系，有：

(14)

式中下标xini和xfin分别代表初态和终态中各相组分的物质的量分数保持不变，SB为组分B的偏摩尔熵。将式(13)对温度求偏导，并代入式(14)，便得：

此式即为式(1)。

推导②：一个更为简单的推导方法是从下列电化学系统的热力学基本方程[3]出发：

(15)

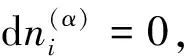
(16)

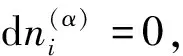
(17)

式中下标2代表终态。因此有：

(18)

若电池反应是从ξ=0的初态进行到ξ=1mol的终态，则式(18)可表示为：

此式即为式(1)。

2 问题二：原电池可逆做电功时吸收的热QR应该怎样表示？

由于ΔrGm=-zFE，将它代入式(1)，可得：

(19)

因此，在一般物理化学教材中几乎无例外地有以下表示：

(20)

但是，这个公式是不恰当的，这可从式(20)中QR的单位看出。因为按照这个公式，QR的单位应为C·mol-1·V，即J·mol-1。而SI制规定，热量的单位只能是焦耳(J)[4]。尽管式(20)的意义是反应进度ξ=1mol时，原电池可逆做电功时吸收的热量，但是将热量的单位与摩尔热力学能一样表示为J·mol-1，这将使系统与环境传递的热量与物质的热力学能混为一谈，从而促使人们联想起早已被推翻的“热质论”，这样的表示显然是不可接受的。

我们认为，正确的表示是将式(19)改写成：

因此，

(21)

积分后得：

(22)

式中S0为积分常数。

已知，ξ=0时S=S0，所以有：

(23)

故原电池可逆做电功时吸收的热量当为：

(24)

由于ξ的单位为mol，这样QR的单位就不再是J·mol-1，而是J，符合SI制的规定。因此，式(24)才是QR的正确表示式。

参 考 文 献

[1] 杨喜平,刘建平,杨新丽,等.大学化学,2011,26(3):38

[2] Reid C E.Chemical Thermodynamics.New York:McGraw-Hill,1990

[3] 胡英,吕瑞东,刘国杰,等.物理化学.第5版.北京:高等教育出版社,2007

[4] 理科化学教材编审委员会物理化学编审组.物理化学教学文集.北京:高等教育出版社,1986