颗粒材料剪胀性的微观力学分析

秦建敏 ，迟璐璐

（1. 大连大学 土木工程技术研究与开发中心，辽宁 大连 116622；2. 大连理工大学 工业装备结构分析国家重点试验室，辽宁 大连 116024）

1 引 言

剪胀现象是由 Reynolds[1]于 1885年首先指出的，他把颗粒材料由剪切应变引起体积变形这一特性称为剪胀性。1936年由Casagrande[2]应用于土力学领域，并分析了土体中摩擦角对体积应变的影响。Rowe[3]采用微观分析方法，基于规则排列结构的研究，通过对内功率的无约束最小化提出了著名的膨胀函数，得到三维空间的表达其中，σ1、σ3分别为大、小主应力，φu为颗粒间摩擦角，V为颗粒体的体积，和分别为体积和轴向应变的变化率。在这一理论中，剪胀性被假设为应力比的单一函数，推导过程中颗粒系统被假设为等效连续体，不考虑颗粒接触处静态和动态约束条件的限制。文献[4]中证实了Rowe的应力剪胀理论中的原理，并提出描述颗粒材料各向异性的一个概念性方法，发现有关结构各向异性演化的一些非常重要的事实，比如大变形后土体接近一个极限各向异性状态。文献[5]基于光弹材料及圆铝棒的直剪试验结果，从颗粒接触点数分布变化规律出发，推导出滑动面上的应力剪胀性方程。文献[6]用离散元方法研究了土体的应力剪胀方程。文献[7]建立了一个“砂土样品”的颗粒力学模型，探讨了剪胀性的颗粒力学影响因素。但室内试验资料证明，膨胀性不仅依赖于应力比，还与材料的内部状态变量有关，如孔隙比。在同样的应力比条件下，排列密实的颗粒体发生剪胀，疏松的颗粒体发生剪缩。至今，颗粒材料的剪胀性仍未得到充分解释，现有的剪胀理论与试验观测结果仍有显著背离，关于颗粒材料剪胀性的演化过程也鲜有报道。

由于颗粒材料所表现出来的变形特性取决于内部颗粒之间、颗粒与孔隙及其他边界之间的相互影响，是其系统内部各种材料结构要素共同作用的结果。因此，本文将从颗粒材料的内部结构入手，用孔隙胞元（void cell）描述颗粒材料的最小单元，进行双轴剪切试验，给出剪切过程中孔隙胞元体积变形的空间分布和演化过程，探讨颗粒材料的膨胀性对加载过程中应力比与内部结构的依赖关系，解释排列密实颗粒材料在剪切过程中先压缩后膨胀的微观机制。

2 孔隙胞元系统

颗粒体系的宏观变形和力学特性，通常不是单个颗粒对外荷载的反应，而是颗粒在空间排列起来对外荷载的反应。因此，在研究颗粒材料的剪胀性之前，必须先明确颗粒体系内部的微观结构。为了描述颗粒体系的分布特性，需要根据颗粒空间的几何信息、粒间接触关系将其划分成几何系统。二维颗粒体的微观拓扑结构可以由颗粒（顶点）、接触（边）和孔隙胞元（面）构成。颗粒系统划分成微元存在一定的任意性，以二维情况为例，点a和b是以O为中心的颗粒的两个接触点，如果点a和b处颗粒表面的切线相交，则接触点a和b称作是一组关联接触。a和b以及颗粒中心O形成一个半开放的子平面 a-O-b，相邻颗粒的子平面连接形成一个闭合空间，如颗粒O、P、Q和R的子平面形成的闭合空间为OaPcQdRbO，称为孔隙胞元，如图1中阴影所示。以4 000个圆形颗粒为例，对颗粒体系中所有颗粒进行循环，生成孔隙胞元系统（void cell system），如图2(b)所示。

从孔隙胞元的构建过程看出，孔隙胞元的边界提供了传递接触力的连续路径，因此，孔隙胞元是承受外部应力时保持稳定的最小单元[8]。将颗粒材料视为具有不同特性孔隙胞元的集合，颗粒材料的力学响应可从孔隙胞元在承受外载时的响应来研究。

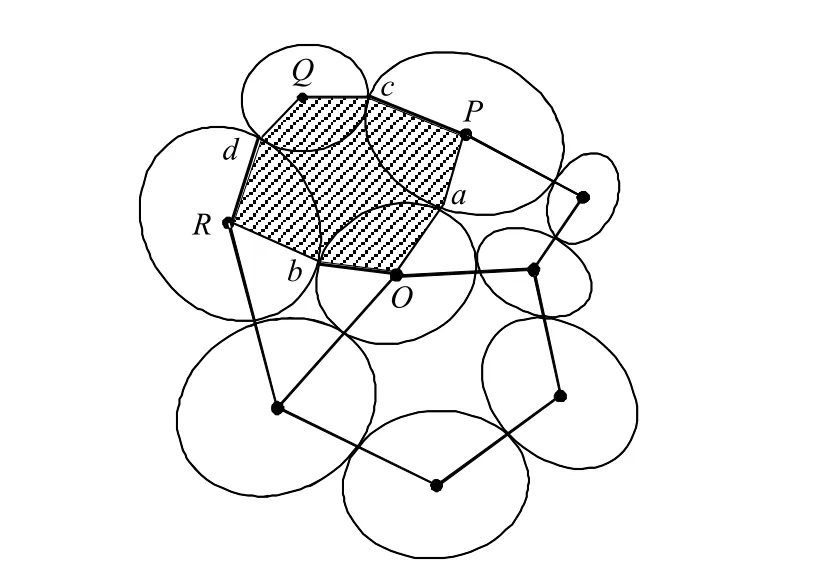
图1 孔隙胞元的构建Fig.1 Construction of void cell

图2 4 000个随机排列的密实颗粒体模型Fig.2 Initial arrangement of dense granular assembly of 4 000 particles

为了方便说明，以图3所示的二维等径颗粒体的规则排列为例进行分析，假设颗粒为刚性体，单个颗粒的变形通过接触点变形来刻画，不考虑颗粒的破碎。研究规则排列的等径颗粒体，有助于揭示颗粒介质力学行为的内在机制。对于规则排列，其力学特性可通过分析代表性孔隙胞元（如图中阴影区域所示）来展开讨论。记其竖直方向和水平方向的长度分别为l1和l2，它们的比值l1/l2称为孔隙胞元的形状因子，定义 α= arctan(l1/l2)以描述周期性结构的几何特征，β表示接触点发生滑动时的角度。作用于试样边界的力与内部接触力平衡，接触力包括法向和切向分量，F11、F22以及F12、F21分别为作用在颗粒上的法向、切向力。颗粒间的摩擦力提高了颗粒体系在承受外荷载时保持稳定的能力。规定以周期性结构受压为正，竖直方向为大主应力方向，记为σ11；水平方向为小主应力方向，记为σ22。

图3 二维规则排列的颗粒体Fig.3 Two dimensional granular assembly with regular arrangement

当孔隙胞元受竖直方向的剪切荷载时，即σ11/ σ22＞ 1，l1/l2减小，孔隙胞元体积发生改变。仅仅从几何上考虑，当孔隙胞元为各向同性时，其面积最大；各向异性越强，面积越小。以四边形为例，孔隙胞元的面积为，当α=45°时，即l1=l2为正方形，面积最大。因此，受剪切荷载作用（ σ11/σ22＞1）时，在基本构型不变的前提下，对于l1/l2>1的孔隙胞元，面积增大，孔隙胞元呈膨胀性；而对l1/l2<1的孔隙胞元，接触点的滑动导致孔隙胞元面积的减小，为压缩的。图3中阴影部分孔隙胞元的剪切过程如图4所示，即从图4(a)～(c)经过先膨胀后压缩的过程。图4(a)和图 4(c)为相同孔隙比条件下孔隙胞元的两种最基本状态，对于α＞45°时的状态图4(a)，大主应力方向与孔隙胞元的方向平行，结构相对稳定，需要承受较大的主应力比才能使原有结构发生破坏，演变为图4(b)的状态，孔隙胞元面积增大；而在α＜45°的图 4(c)状态，孔隙胞元的结构不稳定，只需要较小的主应力比就能使α继续减小，孔隙胞元的孔隙比也减小。因此，孔隙胞元的体积变化与所受应力比和形状因子都有关系。孔隙胞元的形状因子不能增加到无穷大，当形状因子太大时，孔隙胞元可能不能承受外部荷载。在持续的剪切荷载作用下，孔隙胞元的构型发生改变，这时在竖向有新的接触形成，接触力的传递路径因而发生改变，微观结构重新排列。

图4 四边形孔隙胞元的剪切变形Fig.4 Shear deformation of quadrangular void cell

3 离散元双轴剪切试验

本文采用基于孔隙胞元的离散元方法，对颗粒体试样进行双轴剪切试验，详细理论介绍见文献[9]，限于篇幅，本文不再重复介绍。高质量的颗粒体试样必须满足以下3个条件：①颗粒体须满足统计上的各向同性和均匀性；②颗粒体初始状态时的重叠量不宜过大；③在初始状态，必须保证颗粒体处于平衡。本文采用压缩边界法生成颗粒体集合：首先，将颗粒体边界范围按照一定的倍数放大，根据颗粒的级配曲线生成一系列的颗粒；然后，将周围边界压缩，得到设定的孔隙比；最后，使颗粒在非平衡力的作用下自由运动，并在给定的边界范围内达到平衡状态。取如图2中排列致密的4 000个粒径不等的圆形颗粒体为研究对象，对该试样进行双轴剪切试验。试样为高、宽度均为60 mm的正方形，颗粒的粒径在（0.45～1.40）D50之间随机分布，其中D50=1.1 mm，为颗粒体的中值粒径，表示当小于某粒径的土粒质量累计百分比为50%时的粒径。不均匀系数Cu=1.69。试样的初始状态为紧密、随机、各向同性排列，初始孔隙比为0.154，颗粒的初始重叠量为 1.01×10-2D50。颗粒体四周均采用周期性边界，颗粒重度为20 kN/m3，颗粒之间的摩擦系数为0.5（颗粒间摩擦角φ=26.57°），法向接触刚度为2.5×108N/m，切向刚度与法向刚度的比值为0.25，时间步长取 1×10-6s。在双轴加载过程中，颗粒体试样的高度以恒定的速度减小，采用伺服应力控制原理使水平应力σ22保持常数值。

图5给出了排列密实的颗粒体在双轴加载过程中应力比（ q=σ11/σ22）、孔隙比与轴向应变之间的关系曲线。从图 5(a)可以看出，加载过程分为如下几个阶段，即：硬化阶段（A- B- C）、峰值状态（点C）、软化阶段（C- D）、临界状态。在加载初期，颗粒体的力学性能接近于弹性，随着加载的进行，应力比逐渐增大，达到峰值后发生软化，软化现象的发生是由于密实颗粒之间有咬合力，剪切过程中咬合力被破坏，强度降低。随着加载的进一步进行，应力比达到稳定状态保持不变。从图5(b)发现：在初始加载阶段，颗粒体的孔隙比首先发生轻微的下降，然后随着变形的增大，排列致密的颗粒体发生膨胀，并且剪胀现象一直伴随在随后的加载过程中（硬化－达到峰值－软化），直至达到稳定态，孔隙比变化率很小，即达到临界状态。为了说明加载过程中颗粒材料的体积变化不仅与应力比有关，选出图5(a)应力比-应变关系曲线中应力比相同的B和D两点作为比较，详细讨论见第4部分。

4 剪胀性演化过程

下面详细讨论颗粒材料在细观尺度上，即单个孔隙胞元尺度上的变形情况。对颗粒材料应变张量的微观定义具有多样性，大致分为两类：①基于等效几何图形的应变定义，即颗粒体系可以视为等效连续体，假设相应颗粒中心的位移集中发生在接触点处，在均匀场的假设下，建立位移梯度张量与颗粒位移以及相关几何量的关系；②基于最优拟合的应变（best-fit strains），即基于平均位移梯度（应变）拟合出颗粒体系的位移场，寻找位移场与颗粒体系的特征位移偏差最小的平均位移梯度。在这里，特征位移可以选取颗粒中心的平动位移或接触点处的相对平动位移。理论和计算结果表明，基于等效几何图形和颗粒平动位移的细观应变定义与基于材料边界变形的应变更为接近。本文用Kruyt等[10]提出的基于Satake的图形系统定义的适用于二维颗粒物质的表达式。

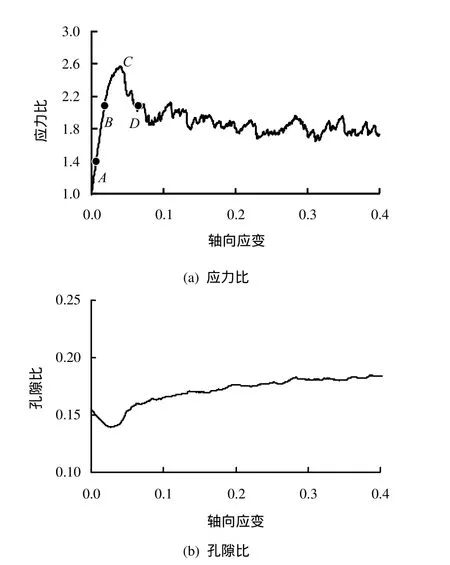
图5 应力比和孔隙比与轴向应变的关系曲线Fig.5 Stress ratio and void ratio vs. axial strain

二维颗粒体区域S的拓扑结构可以分成n个多边形子结构 Si的集合，每个子结构表示由接触颗粒的接触支链围成的孔隙胞元，如图6所示。整个颗粒体区域S的变形率可由速度梯度L表示，L为位置x的函数，L在宏观尺度上是均匀的，而微观尺度（即每个孔隙胞元）上的有较大的变化。整个区域的平均速度梯度与每个孔隙胞元的平均速度梯度有如下关系：

Kuhn假设速度沿着孔隙胞元的边是线性变化的，推导出具有m条边的多边形孔隙胞元Si的的表达式如下[11]：

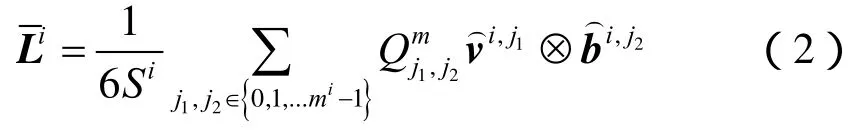
图6 粒子图和对应第i个孔隙胞元的矢量图Fig.6 Particle graph and the vectors in the corresponding i th void cell

图7给出了初始排列为密实状态的颗粒体在双轴剪切过程中，孔隙胞元及其内部体积变形的演化过程。图中ε22为轴向应变，q为应力比。从图7中的离散元数值结果可以看出，局部孔隙胞元的变形具有明显的非均匀性，这从图中的颜色差异可以体现出来。以蓝色填充的孔隙胞元代表其中的 Φi为正，表示该胞元内的变形为膨胀；以红色填充的孔隙胞元中的变形率为负，该孔隙胞元内的变形为压缩。比较图7中各个不同加载阶段发现，在双轴加载过程中，颗粒体内部孔隙胞元的形状发生改变，并存在由体积变化较大的孔隙胞元形成的窄带。在初始加载状态，孔隙胞元的形状基本为各向同性，颗粒材料内部几乎所有的孔隙胞元内体积应变都是压缩的（如图7(a)、(b)所示），这与前面图5(b)中相同轴向应变时孔隙比的变化一致。结合图4中四边形孔隙胞元的3种基本状态，在加载初期，图4(a)状态的孔隙胞元保持不变，而处于图 4(c)状态的孔隙胞元发生变化，持续加载使α变小，从而孔隙胞元面积变小，即孔隙比变小。初始状态越密实的颗粒材料，处于图4(c)状态的孔隙胞元对于加载初期的剪缩现象的贡献就越大，这就是在加载初期排列密实的颗粒材料会发生剪缩现象的原因。随着加载的进行（如图7(c)所示），孔隙胞元在竖直压缩方向上变大，孔隙胞元的几何形状出现各向异性；接触力较大的力链沿着近似平行于大主应力的方向（即竖直方向）排列，形成柱状结构，荷载沿着相对较强的力链传递，此时孔隙胞元结构相对稳定，总体的应力-应变关系曲线为硬化状态（对应图5(a)）；孔隙胞元内部体积变形大部分为压缩（对应图5(b)中孔隙比与轴向应变关系曲线中也为压缩），由压缩变形大的孔隙胞元组成窄带，窄带中的局部孔隙胞元内压缩变形略微大于周围孔隙胞元的压缩性。随着加载的进行，颗粒体内部孔隙胞元的结构进一步改变，由于颗粒体在水平方向上持续膨胀，颗粒材料发生剪胀，孔隙胞元内部体积变形大部分为膨胀，由膨胀性大的孔隙胞元组成了窄带（如图7(d)所示），持续剪胀使内部很多孔隙胞元解体，颗粒体的力学响应进入软化状态。比较图7(b)和图7(d)，虽然颗粒体所处的应力水平相同，但是由于在加载过程中，颗粒体内部孔隙胞元的几何结构发生了很大的变化，微观尺度上体积变形也有很大的不同，其对应的宏观尺度上力学响应也有明显的区别。

图7 颗粒体孔隙胞元内的体积变形Fig.7 Volume deformation in individual void cell of particulate assembly

5 结 论

以单个孔隙胞元描述颗粒材料的内部结构，分析了承受剪切荷载时其体积变化与孔隙胞元形状、所受应力状态的关系。对排列致密的颗粒材料进行离散元双轴剪切试验，得到了不同加载阶段孔隙胞元系统的演化过程。

（1）微观尺度上孔隙胞元内体积存在先压缩后膨胀、形状上先各向同性后沿主应力方向变长的现象，体积变形同时受孔隙胞元形状及所受应力状态二者的影响。

（2）在剪切过程中，孔隙胞元的体积变形存在局部化现象，由体积变形较大的孔隙胞元组成倾斜的窄带。

（3）综合孔隙胞元的受力分析和离散元数值结果表明，致密排列颗粒材料的剪胀性与微观尺度上孔隙胞元的几何结构及其内部的力链传递方式密不可分。

[1]REYNOLDS O. On the dilatancy of media composed of rigid particles in contact, with experimental illustrations[J]. Philosophical Magazine (Series 5), 1885,20: 469－481.

[2]CASAGRANDE A. Characteristics of cohesionless soils affecting the stability of slopes and earth fills[J]. Journal of the Boston Society of Civil Engineers, 1936, 23(1):257－276.

[3]ROWE P W. The stress dilatancy relation for static equilibrium of an assembly of particles in contact[J].Proceedings of the Royal Society of London (Series A):Mathematical and Physical Sciences, 1962, 269: 500－527.

[4]HOME M R. The behavior of an assembly of rotund, rigid,cohesionless particles[J]. Proceedings of the Royal Society of London (Series A): Mathematical and Physical Sciences, 1965, 286: 62－97.

[5]MATSUOKA H. A microscopic study on shear mechanism of granular materials[J]. Soils and Foundations, 1974, 14(1): 29－43.

[6]LIU S H, MATSUOKA H. Microscopic interpretation on a stress-dilatancy relationship of granular materials[J].Soils and Foundations, 2003, 43(3): 73－84.

[7]常在, 杨军, 程晓辉. 砂土强度和剪胀性的颗粒力学分析[J]. 工程力学, 2010, (4): 95－104.CHANG Zai, YANG Jun, CHENG Xiao-hui. Granular mechanical analysis of the strength and dilatancy of sands[J]. Engineering Mechanics, 2003, 43(3): 73－84.

[8]秦建敏, 张洪武. 颗粒材料的微观临界状态理论模型[J]. 岩土力学, 2010, 31(12): 3697－3703.QIN Jian-min, ZHANG Hong-wu. Microscopic theoretical model of critical state for granular materials[J].Rock and Soil Mechanics, 2010, 31(12): 3697－3703.

[9]张洪武, 秦建敏. 基于非线性接触本构的颗粒材料离散元数值模拟[J]. 岩土工程学报, 2006, 28(11): 1964－1969.ZHANG Hong-wu, QIN Jian-min. Simulation of mechanical behaviors of granular materials by discrete element method based on mesoscale nonlinear contact law[J]. Chinese Journal of Geotechnical Engineering,2006, 28(11): 1964－1969.

[10]KRUYT N P, ROTHENBURG L. Micromechanical definition of the strain tensor for granular materials.ASME[J]. Journal of Applided Mechanics, 1996, 63(3):706－711.

[11]KUHN M R. Deformation measures for granular materials[C]//Mechanics of Deformation and Flow of Particulate Materials. New York: American Society of Civil Engineers, 1997: 91－104.