隧洞围岩损失位移估计的智能优化反分析
张 研,苏国韶,燕柳斌
(1. 广西大学 土木建筑工程学院,南宁 530004;2. 广西大学 工程防灾与结构安全教育部重点实验室,南宁 530004;3. 广西大学 广西防灾减灾与工程安全重点实验室,南宁 530004)
1 引 言
隧洞施工过程中,监测断面的布置一般滞后于掌子面开挖,监测仪器到位前围岩发生的位移可称为损失位移。损失位移的求取对于围岩稳定性的合理评价具有重要意义,特别是当损失位移较大时,若将监测到的少部分位移作为围岩最终的收敛位移,必然给隧洞的安全性和正常工作性能的评价带来较大的偏差。此外,自新奥法施工理念出现以来,利用围岩位移量测信息进行信息化施工已成为现代隧洞工程施工的一种趋势,然而,在信息化施工过程中,如果忽视损失位移信息,将给施工安全带来不利影响,并会导致围岩反分析结果出现较大误差[1]。因此,如何获取损失位移成为隧洞围岩稳定性评价和安全施工的关键问题。
多年来,人们进行损失位移求解时,常根据经验引入荷载(或位移)释放系数,进而求得相应的等效释放荷载,再依据Boltzmann叠加原理得到监测位移[2],然而荷载(或位移)释放系数一般依靠经验来确定,存在一定的盲目性。近年来,杨志法等[3]考虑松动圈的影响,提出将损失位移求取问题转化为反分析围岩多层分区弹性模量问题,对提高位移反分析精度起到了很大作用;张传庆等[4]以Hoek经验公式的通式为基础,基于现场监测收敛位移曲线,提出了求取损失位移的方法,取得了一定进展。然而由于问题的高度复杂性,现有的理论和方法还难以完全满足工程实践的要求,因此,寻求更为合理有效的围岩损失位移求取方法是很有必要的。
监测收敛位移是隧洞开挖过程中获得的最直接、最有效的信息,以监测位移作为优化反分析的依据是损失位移求取的有效途径。本文在数值方法的基础上,将损失位移的求取问题转化为一种优化反分析问题,然后再利用优化方法进行求取。
由于岩体结构的复杂性,优化反分析的目标优化函数常是一种复杂的非线性多峰函数,采用传统的梯度优化方法往往只能获得局部最优解。近年来,采用遗传算法(genetic algorithm,GA)、粒子群优化算法(particle swarm optimization,PSO)等随机性全局优化算法求解优化反分析问题成为了一种趋势[5-6]。但采用随机性全局优化算法时,为了评价随机解的优劣,往往需要对大量的随机解进行成千上万次的适应度评价。由于岩体结构的复杂性,很难建立决策变量与适应度函数的显式表达式,往往需要借助数值计算建立这种隐含关系,而数值计算是相对耗时的,多次的适应度评价使得总的计算耗时过于浩大,从而导致随机性全局优化算法在工程应用中受到了极大限制。为了有效地减少优化过程中适应度评价次数以提高损失位移优化反分析的求解效率,本文将 PSO[7-8]、高斯过程机器学习方法(Gaussian process,GP)[9-10]、FLAC3D数值计算方法[11]相结合,提出隧洞围岩损失位移反分析的PSO-GP-FLAC3D方法,为隧洞围岩损失位移求取提供一条新的途径。
2 损失位移优化反分析的计算模型
2.1 损失位移优化反分析的总体思路
假设有一隧洞,借助数值计算模型,容易获得开挖后围岩某测点的计算位移u随时间t变化的全过程曲线,即位移全收敛计算曲线。保持计算模型和本构关系不变,给定不同的围岩力学参数能够计算获得不同的位移全收敛计算曲线。同时,将实测位移依照对应的监测时间描绘于同一坐标系中,该测点的两条位移全收敛计算曲线和一条位移实测曲线见图1。以实际位移监测开始时刻为分隔点,图1中的两条位移全收敛计算曲线均可分为两部分:一部分是损失位移,另一部分是监测位移。从图中可看出,与计算曲线1相比较,计算曲线2的监测位移部分与位移实测曲线较接近,由此可认为,计算曲线2的可信度较高,进而可以推断计算曲线2包含的损失位移即为可能的损失位移。如何获取计算曲线 2,就成为了问题的关键。可以采用优化反分析方法来推求曲线 2,这时损失位移的求解就转化成一种优化反分析问题。
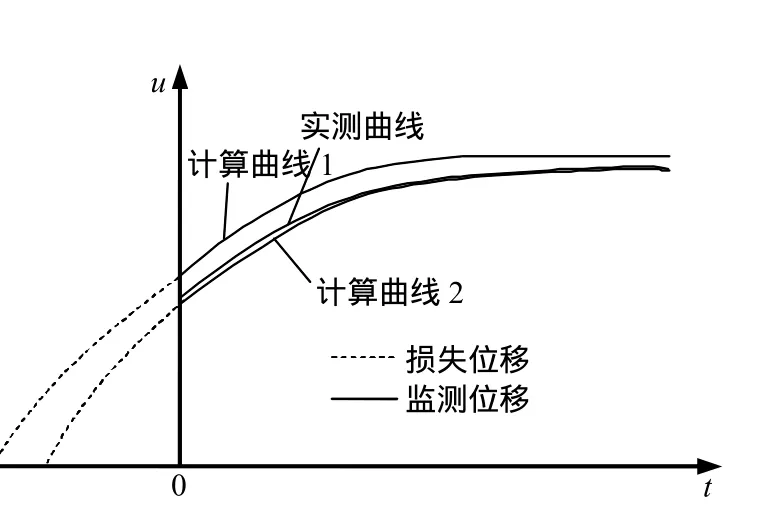
图1 围岩位移变形曲线Fig.1 Displacement curves of surrounding rocks
2.2 优化反分析的目标函数与决策变量
优化反分析以计算位移曲线与实际监测位移曲线的误差最小化为优化目标,以围岩力学参数为决策变量,通过优化参数,搜索出计算位移曲线与实际监测位移曲线最为接近的位移全收敛计算曲线,该曲线中包含的损失位移部分即为相对可信的损失位移。
为了评价计算收敛位移曲线与实际监测收敛位移曲线的接近程度,依据监测时间确定用于比较的样本点。由此,优化反分析的优化目标函数可设为
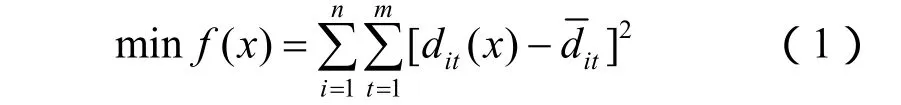
式中:f(x)为目标函数;x为决策变量;m为监测总时间;n为位移测点总数;dit为第i个位移监测点在t时刻的位移计算值;为第i个位移监测点在t时刻的位移实测值。
约束条件为

式中:常数a、b分别为决策变量取值区间的下限和上限。
建立上述优化问题的优化目标函数与约束条件后,就可采用优化方法进行求解。
3 损失位移优化反分析智能优化方法
3.1 粒子群优化方法
PSO算法最早由Eberhart和Kennedy博士首先提出[7],它是模拟鸟类群体捕食行为的一种仿生智能优化算法。由于其具有算法简单、寻优能力强等优点,近年来受到各个领域学者的关注。
算法首先随机初始化一群粒子,然后调整速度、位置,通过多次迭代来寻找最优值。在每次迭代中,粒子通过跟踪本身迄今为止寻找到的最优值,即个体极值Pid;当前整个粒子群找到的最优值,即全局极值 Pgd,以及粒子前一次迭代的状态来调整当前迭代步的位置和速度。粒子速度和位置的调整方程为

式中:vid(k)为第i粒子在第k次迭代中第d维度上的速度;xid(k)为第i粒子在第k次迭代中第d维度上的位置;c1和c2均为学习因子,通常c1=c2=1.8~2.0;r1、r2为(0,1)之间的均匀分布的随机数;w为惯性权重。为了避免算法后期在全局最优解附近难以收敛这个问题,w值应随算法迭代的进行而减小,一般依据下式进行线性减小:

式中:wmax、wmin分别为最大、最小惯性权重;t为当前迭代数;tmax为最大迭代数,一般wmax=0.9,wmin=0.4。
3.2 高斯过程机器学习方法
GP是基于高斯随机过程与贝叶斯学习理论发展起来的一种新的机器学习方法。由于其具有良好的适应性,能够很好地处理高维数、小样本、非线性等复杂问题,近年来得到广泛应用[12-13]。在保证性能的前提下,与神经网络(ANN)和支持向量机(SVM)相比,高斯过程具有灵活的非参数推断、参数自适应获取、实现过程简单等突出优点。
以统计学理论的观点分析,GP是随机变量的1种集合。其任意有限随机变量集合均服从联合高斯分布,即对任意一组n维随机变量X,与其对应的t时刻的过程状态()fX 的联合概率分布是n维高斯分布。当给定它的均值m(t)和协方差函数 k(t,t′)时,()fX 在t时刻的过程状态()f t完全确定,GP定义式表示如下:
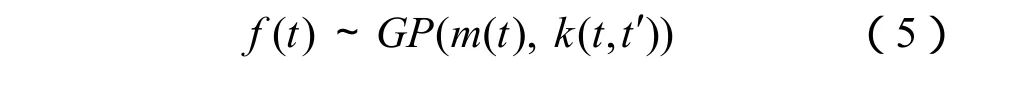
假设有 n组观察数据的集合 D={(xi,yi) |i=1,...,n}作为GP模型的训练样本集合,其中:xi为d维输入矢量,yi∈R为观察目标值。如果X为d×n维输入矩阵,y表示输出矢量,那么训练样本集合可表示为D=(X,y)。
对于新的d维输入矢量 X*,学习过的GP模型可以依据先验知识预测出与X*相对应的输出矢量y*。
实际建模过程中通常要考虑噪声的影响,则带高斯噪声的标准线性回归模型为
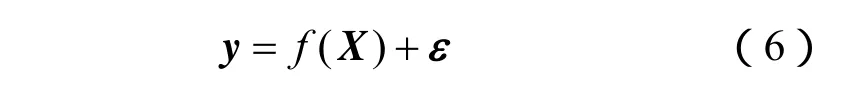
式中:f(X)为回归函数值;ε为噪声,且符合均值为0、方差为的高斯分布。
根据贝叶斯学习理论,观察目标值y的先验分布为

式中:(=K K X,)X 为n×n阶对称正定的协方差矩阵,矩阵中的任一项kij度量了xi和xj的相关性;I为单位矩阵。
n个训练样本的观察目标矢量y和1个测试样本的回归函数输出值f*所形成的联合高斯先验分布为
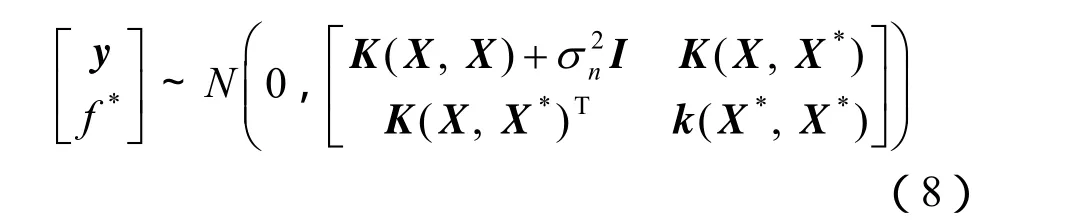
式中:K(X,X*)为测试点 X*与训练样本集合的所有输入点X的n×1阶协方差矩阵;k(X*,X*)为测试点 X*本身的协方差矩阵,可分别简写为K(X*)、k(X*)。常用的协方差函数为
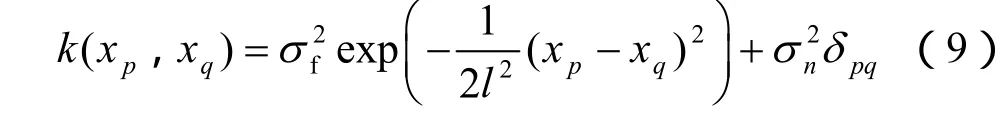
式中:超参数l、σf、σn的选取对学习与预测结果的影响较大。在GP回归模型中,最优超参数可采用极大似然法自适应获得[9];xp、xq根据情况可以是训练样本之间、测试样本之间或者训练样本与测试样本之间的变量组合;δpq是符号函数,当p=q时,δpq=0,反之 δpq=1。
GP学习完成后,将根据贝叶斯原理在训练集先验分布的基础上预测出与X*对应的最可能的输出值。贝叶斯原理能够利用观察到的真实数据不断更新概率预测分布,当给定新的输入 X*、训练集的输入值X和观察目标值y的条件下,推断出f*预测值的均值和方差为
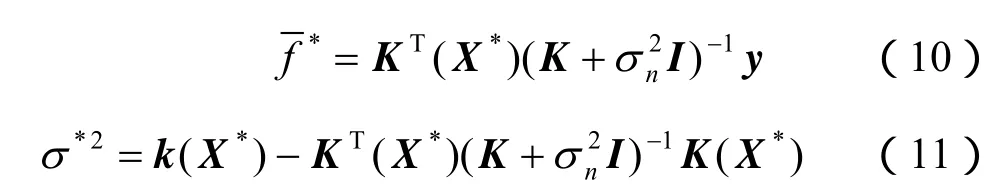
3.3 PSO-GP-FLAC3D优化反分析方法
3.3.1 方法构建的思路
采用粒子群优化-高斯过程协同优化方法[14],结合FLAC3D数值计算软件进行损失位移优化反分析。其中,将式(1)作为适应度函数。
为了进一步提高优化反分析的效率,本文对粒子群优化-高斯过程协同优化方法做了如下的改进。
(1)对于全局最优解的超前预测
原方法在每次循环中仅利用一次GP机器学习模型在全局空间下对可能最优解进行预测,本文通过构建内层循环,循环产生q(q=1,2,…,q)代粒子(q为内循环次数),多次采用GP机器学习模型对粒子适应度进行评价,并寻找q代粒子中适应度最小的粒子即全局空间下预测可能最优解,作为预测全局最优解。这样就能充分发挥GP机器学习模型对粒子适应度进行评价,无需调用数值计算这一优点,提高寻找全局最优解的效率。
(2)对于寻优经验知识库的动态更新
原方法是将当前迭代步的最优粒子信息作为新的知识源添入知识库,而本文对寻优经验知识库的更新从以下两个途径实现:①对q代粒子中适应度最小的粒子进行了一次真实适应度评价,不浪费此次适应度评价,将该粒子个体信息作为新的知识源替换寻优经验知识库中最差粒子,更新寻优经验知识库;②当不满足精度要求进入外循环时,在最优粒子指引下主粒子群结构产生第2+p(p=0,1,…,p)代粒子(p为外循环次数),经过适应度评价,将此代粒子信息与原寻优经验知识库的所有样本信息按照适应度由小到大顺序进行排列,选择与原知识库数量相等的适应度较小的粒子组建新的寻优经验知识库。与原方法相比,通过保持知识库的容量不变并提高知识库质量,可以明显提高GP模型的预测能力与精度。
(3)此外,本文方法采用双层嵌套的粒子群结构,充分利用粒子群自身寻优技术,降低对粒子群寻优结构的破坏,大大提高粒子群获得最优解的机会,而原方法采用的搜索空间动态压缩、全局最优解随机扰动等措施,需要干扰粒子群本身寻优,增加了算法的难度。
3.3.2 方法的实现步骤
本文方法的流程图见图 2,其框架主要由两个嵌套的粒子群算法组成,主粒子群结构由外层循环构建,内层循环构建子粒子群结构。具体实现步骤如下:
(1)应用FLAC3D数值计算软件建立隧洞数值计算模型,采用某种岩体流变本构模型,将其参数作为决策变量。编制Fish程序,选取测点、监测时间,依据式(1)建立适应度函数。
(2)启动 MATLAB环境下的优化程序,根据决策变量的个数设置PSO算法的维数。为了保证随机解的互异性,依照粒子群规则随机初始化第1代和第2+p代粒子作为随机解(p为动态更新最优粒子的循环次数)。调取FLAC3D程序,将随机解作为岩体的计算力学参数,通过FLAC3D获取各测点的计算位移,将各测点的计算位移代入适应度函数,获得每个粒子的适应度,然后返回 MATLAB环境下的优化程序,对随机解的适应度进行比选。如果最小适应度满足精度要求,则退出计算,最小适应度对应粒子即为最优解;否则,转入下一步。
(3)当步骤(2)中p=0时,基于第1代和第2代粒子建立寻优经验知识库;当p≠0时,更新寻优经验知识库。接着,将知识库中适应度最小粒子作为历史最优解。
(4)根据PSO规则在内循环产生第q代粒子,采用GP机器学习模型对知识库中样本进行学习,初步建立自变量与函数值的非线性映射关系。借助学习后的GP模型取代FLAC3D计算对此代粒子进行适应度预测,通过q次循环选取预测适应度最小粒子作为基于GP模型的最优解的预测值。
(5)考虑到最优解的预测值与数值计算解之间必然存在一定的误差,将最优解的预测值代入FLAC3D进行正向计算,将此解获得对应的真实的适应度函数值返回 MATLAB环境下,并与当前迭代步历史最优解的适应度进行比较,较小者为当前迭代步对应的当前最优解。将当前最优解返回寻优经验知识库,动态更新寻优经验知识库。
(6)对当前最优解进行精度判断,如果满足精度要求,则退出计算;反之,则动态更新最优粒子,循环次数p增加一次,指导主粒子群结构产生下一代粒子,引领粒子群飞向最有前景的寻优方向。同时,将此新一代粒子经过适应度评价产生的新信息与原寻优经验知识库的所有样本信息,按照适应度由小到大顺序进行筛选,选取与原知识库中同样数目的样本更新知识库。按照上述两种策略动态更新寻优经验知识库,克服随机优化算法过度依赖初始学习样本这一局限性,保证算法的全局性。
依据上述步骤编制了MATLAB计算程序,程序中采用接口程序直接调用FLAC3D数值计算程序。
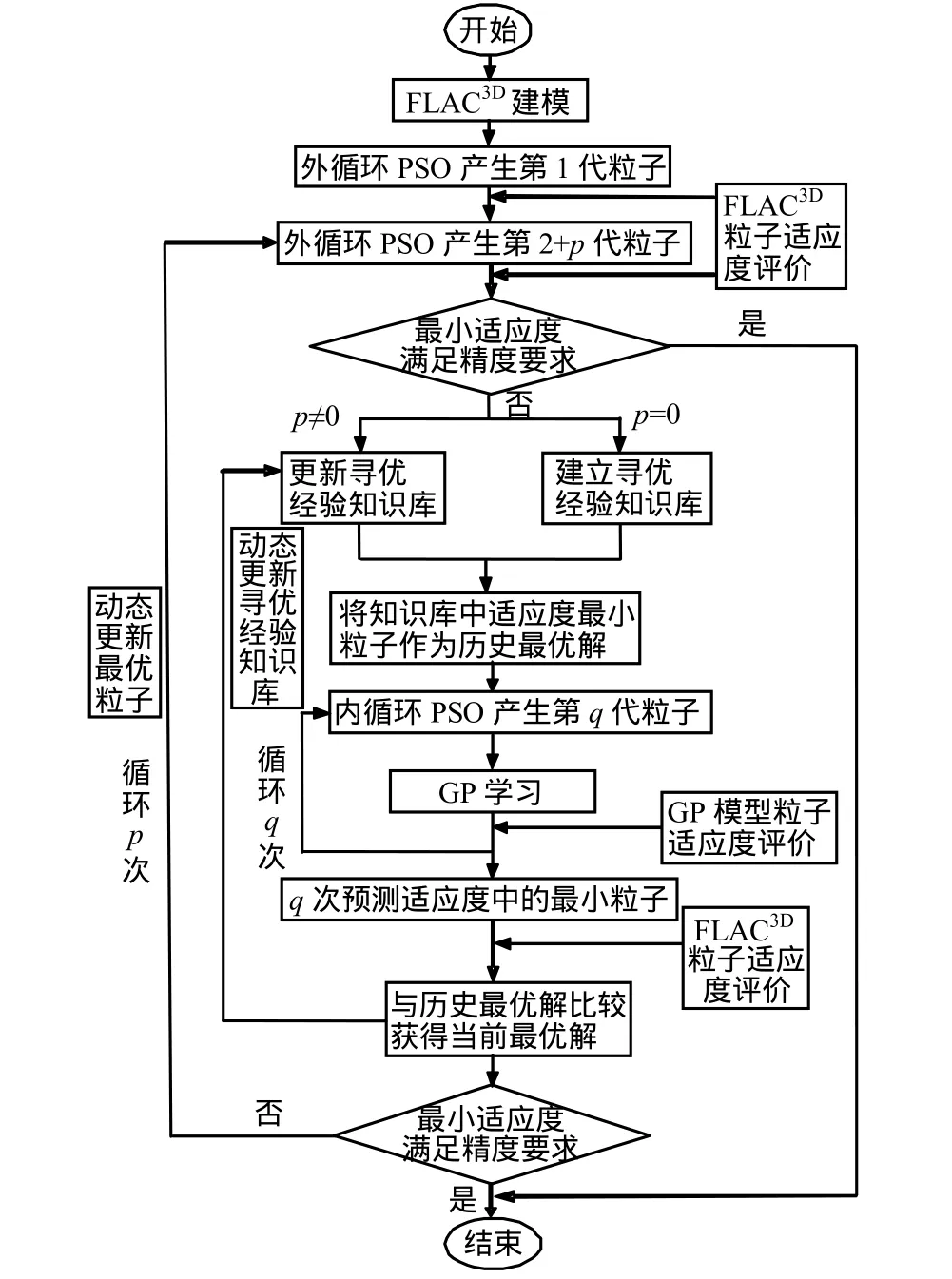
图2 PSO-GP-FLAC3D方法流程图Fig.2 Flow chart of PSO-GP-FLAC3D method
4 算例研究
为了验证上述方法的可行性,分别采用标准PSO-FLAC3D与PSO-GP-FLAC3D方法求取隧洞围岩损失位移。取1/4圆形隧洞如图3所示,隧洞直径为20 m,隧洞沿坐标轴x、z方向围岩厚度均为90 m,沿 y方向取单位厚度,均质岩性,初始地应力为σx=σy=σz=30 MPa。本构模型采用经典黏弹性本构模型——Viscous模型,决策变量为泊松比μ、弹性模量E和黏滞系数η共3个变量,则PSO的维数为3维。作为例证,沿环向分别在 30°、45°、60°处选取3个测点a、b、c作为监测点(见图4),真解设为:μ=0.2,E=2.0 GPa,η=10 GPa·d,总的计算时间为10 d,滞后监测为4 d,即实际监测总时间为6 d。将后6 d测点计算位移作为实测位移,采用本文方法预测前4 d测点已发生的损失位移。
目标函数即适应度函数参见式(1),其中:监测总时间m=6 d;位移测点总数n=3;两种方法的搜索范围设为:0.1≤μ≤0.5,1.0 GPa≤E≤5.0 GPa,8.0 GPa·d≤η≤12.0 GPa·d。

图3 隧洞网格划分图Fig.3 Mesh of tunnel

图4 隧洞开挖面的测点布置图Fig.4 Monitoring points of excavation section for tunnel
以精度满足f<1×10-4作为终止条件,标准PSO算法参数设置:维数 D=3,种群个数 NP=30,c1=c2=2.0,p=500,最大飞行速度Vmax= [0.01,0.01,0.01]。PSO-GP-FLAC3D模型中PSO的参数设置同标准PSO算法,q =10,GP模型初始超参数lnl =[-1,-1,-1],lσnf=-1,σn=1×10-6。
为了保证两种算法对比的公平性,每种算法都独立运行5次,取其适应度评价次数的平均值作为该算法的最终适应度评价次数。计算结果见表 1,两种方法的相对误差令人满意。但与标准PSO方法相比,采用PSO-GP-FLAC3D方法时计算代价得到了大幅度削减,适应度评价次数和计算耗时仅为标准PSO-FLAC3D的1/5。

表1 两种方法计算结果比较Table 1 Results comparison with different methods
PSO-GP-FLAC3D方法在3个测点处与实测位移曲线的拟合情况见图5。从图中可见,在3个测点处计算监测收敛位移曲线与实际监测收敛位移曲线基本吻合。最终计算损失位移与实测损失位移大小比较如表 2所示,3个测点中最大相对误差为0.37%,平均相对误差仅有0.32%,说明本文方法是可行的,能够通过对实际监测收敛位移曲线的准确拟合,可获取合理的损失位移。

图5 各测点的计算位移与实测位移对比Fig.5 Comparison between calculated displacement and measured displacement of monitoring points

表2 计算损失位移与实测损失位移比较Table 2 Comparison between calculated loss displacement and measured loss displacement
为了探讨滞后监测时间对损失位移预测精度的影响,本文还对滞后监测天数为6、8 d情况下不同测点的损失位移进行预测,计算结果如表3所示。从中可见,滞后监测天数越大,反分析获得的损失位移精度越低。当滞后监测天数达到8 d时,3个测点获取的损失位移相对误差均超过了 5%,计算结果可信度相对较低。
5 工程应用
锦屏二级水电站位于四川省凉山彝族自治州境内的雅砻江锦屏大河弯处雅砻江干流上,系利用雅砻江锦屏150 km长大河弯的天然落差,裁弯取直、凿洞引水建成的。锦屏二级水电站共有引水隧洞 4条,最大埋深为2550 m,为超深埋长隧洞特大型地下水电工程。为了保证隧洞施工的安全性,开挖辅助洞A、B以超前探明地质情况[15]。辅助洞大部分洞段处高地应力区,开挖后围岩应力释放剧烈。下面以辅助洞B的BK14+599断面为例,利用实测位移资料,采用本文方法进行围岩损失位移的优化反分析。

表3 不同监测天数损失位移计算结果比较Table 3 Results comparison of calculated loss displacement for different monitoring days

图6 BK14+599断面的AC测线布置图Fig.6 AC monitoring line of section BK14+599
数值计算网格划分如图7所示,模型的水平x方向与竖直z方向均取60 m,沿隧洞轴线y方向取单位厚度。
图7 BK14+599断面的网格划分图Fig.7 Mesh of section BK14+599
选取AC测线的实测收敛位移,依据式(1)建立适应度函数,其中:监测总时间m=45 d;位移测点总数 n=2;决策变量的搜索范围设为:0.1≤μ≤0.3,1.0 GPa≤E≤12.0 GPa,1.0×104GPa·d≤η≤12.0×104GPa·d。采用本文方法进行求解,相关参数设置与以上算例相同。
经优化反分析,获得的全局最优解是:围岩泊松比μ=0.263、围岩弹性模量E =10.295 GPa、围岩滞系数η=79567.5 GPa·d。测线AC的损失位移达10.45 mm(见图8),占实际总位移的比例高达36%。如果仅依据远小于实际总位移的监测位移来指导隧洞开挖或评价围岩稳定性,将给该隧洞的施工和运行安全带来潜在隐患。因此,该工程由于埋深较大,开挖后的弹性变形大,其引水隧洞及辅助洞的围岩损失位移不可忽视,在围岩稳定性评价中应给予足够重视。
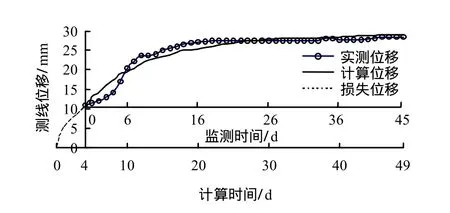
图8 测线AC的计算位移与实测位移对比Fig.8 Comparison between calculated displacement and measured displacement of AC monitoring line
6 结 论
(1)损失位移的准确预测对于地下工程围岩稳定性的合理评价具有重要意义。本文提出了1种损失位移求解的新思路,即根据滞后监测的围岩位移信息,通过优化反分析方法预测监测时刻前已发生的损失位移,并可同时获取合理的围岩计算力学参数。研究表明,该思路是可行的,为围岩损失位移问题的求解提供了一条新的途径。
(2)针对位移全局优化反分析过程计算量较大的问题,本文结合数值计算模型,提出了一种基于高斯过程机器学习与粒子群优化算法的损失位移智能优化反分析方法,算例研究与工程应用表明,该方法是可行的,与传统优化反分析方法和以往智能优化反分析方法相比较,该方法采用动态更新学习样本的策略,具有不依赖初始学习样本的优点,在获取全局最优解的前提下,计算效率具有一定的优越性。
(3)通过算例验证,随着监测天数的减少,获取的损失位移精度降低。在实际应用中,应尽可能早的布置监测仪器,尽可能多的获取监测位移数据,将有利于进一步提高所获取的损失位移的可靠性。算例研究表明,随着滞后监测天数的增加,采用本文方法获取的损失位移的误差也会随着增高。因此,在本文方法的工程应用中,应注意监测滞后天数对预测精度的影响,滞后天数较大时,应适当调整对预测结果的可靠度的预期。另一方面,在开挖后及时布置监测仪器,尽量减小损失位移,将有利于提高围岩损失位移与力学参数反分析结果的可靠性。
(4)锦屏二级水电站辅助洞某断面的损失位移反分析结果表明,损失位移占实际发生总位移的比例高达36%,说明深部地下岩体工程中,受高地应力的影响,开挖后围岩在短时间内弹性变形大,围岩损失位移不可忽视,在围岩稳定性评价与围岩参数反分析中应给予足够重视。
(5)为便于工程应用,本文仅对基于经典黏弹性本构模型——Viscous模型的二维空间围岩损失位移求取方法进行了探讨。在工程应用中,采用本文方法时应考虑工程围岩特点,选择合适的岩体本构模型。此外,隧道围岩变形还受到开挖方式、开挖进尺、支护等多种因素的综合影响。关于多种因素影响下三维空间围岩损失位移反分析问题的研究将另文阐述。
[1]杨林德. 岩土工程问题的反演理论与工程实践[M]. 北京:科学出版社,1996.
[2]蔡美峰,何满潮,刘东燕. 岩石力学与工程[M]. 北京:科学出版社,2002.
[3]杨志法,熊顺成,王存玉,等. 关于位移反分析的某些考虑[J]. 岩石力学与工程学报,1995,14(1):11-16.YANG Zhi-fa,XIONG Shun-cheng,WANG Cun-yu,et al.Some consideration of the back-analysis from displacements[J]. Chinese Journal of Rock Mechanics and Engineering,1995,14(1):11-16.
[4]张传庆,冯夏庭,周辉,等. 隧洞围岩收敛损失位移的求取方法及应用[J]. 岩土力学,2009,30(4):997-1003.ZHANG Chuan-qing,FENG Xia-ting,ZHOU Hui,et al.Method of obtaining loss convergence displacement and its application to tunnel engineering[J]. Rock and Soil Mechanics,2009,30(4):997-1003.
[5]高玮,郑颖人. 采用快速遗传算法进行岩土工程反分析[J]. 岩土工程学报,2001,23(1):120-122.GAO Wei,ZHENG Ying-ren. Back analysis in geotechnical engineering based on fast-convergent genetic algorithm[J]. Chinese Journal of Geotechnical Engineering,2001,23(1):120-122.
[6]赵洪波. 基于微粒群优化的智能位移反分析研究[J].岩土工程学报,2006,28(11):2035-2038.ZHAO Hong-bo. Back analysis of intelligent displacement based on particle swarm optimization[J].Chinese Journal of Geotechnical Engineering,2006,28(11):2035-2038.
[7]李丽,牛奔. 粒子群优化算法[M]. 北京:冶金工业出版社,2009.
[8]KENNEDY J,EBERHART R. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Perth:IEEE Press,1995.
[9]SEEGER M. Gaussian processes for machine learning[J].International Journal of Neural System,2004,14(4):69-106.
[10]SOFIANE B B,AMINE B. Gaussian process for nonstationary times series prediction[J]. Computational Statistics &Data Analysis,2004,47(4):705-712.
[11]彭文斌. FLAC3D实用教程[M]. 北京:机械工业出版社,2008.
[12]苏国韶,宋咏春,燕柳斌. 岩体爆破效应预测的一种新方法[J]. 岩石力学与工程学报,2007,26(增刊):3509-3514.SU Guo-shao,SONG Yong-chun,YAN Liu-bin. A new method for forecasting of blasting effect in rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(Supp.):3509-3514.
[13]苏国韶,燕柳斌,张小飞,等. 基坑位移时间序列预测的高斯过程方法[J]. 广西大学学报(自然科学版),2007,32(2):223-226.SU Guo-shao,YAN Liu-bin,ZHANG Xiao-fei,et al.Time series prediction of foundation pit displacement using Gaussian process method[J]. Journal of Guangxi University(Natural Science Edition),2007,32(2):223-226.
[14]苏国韶,张克实,吕海波. 位移反分析的粒子群优化-高斯过程协同优化方法[J]. 岩土力学,2011,32(2):510-515,524.SU Guo-shao,ZHANG Ke-shi,LÜ Hai-bo. A cooperative optimization method based on particle swarm optimization and Gaussian process for displacement back analysis[J]. Rock and Soil Mechanics,2011,32(2):510-515,524.
[15]刘建友,伍法权,卢丙清,等. 雅砻江锦屏二级水电站皮带输送隧洞施工中的地质问题分析及其处理措施[J].工程地质学报,2009,17(5):591-596.LIU Jian-you,WU Fa-quan,LU Bing-qing,et al.Geological problems encountered in rock tunnel at Jinping Ⅱ hydroelectric power station and their treatment measures[J]. Journal of Engineering Geology,2009,17(5):591-596.
[16]陈炳瑞,冯夏庭,黄书岭,等. 基于快速拉格朗日分析——并行粒子群算法的黏弹塑性参数反演及其应用[J]. 岩石力学与工程学报,2007,26(12):2517-2525.CHEN Bing-rui,FENG Xia-ting,HUANG Shu-ling,et al.Inversion of viscoelasto-plastic parameters based on fast Lagrangian analysis of continuum—parallel particle swarm algorithm and its application[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(12):2517-2525.

