基于等级相关的泥石流危险因子筛选与危险度评价
陈鹏宇,乔景顺,彭祖武,谢 凯,余宏明
(1. 中国地质大学(武汉)工程学院,武汉 430074;2. 黄淮学院 建筑工程学院,河南 驻马店 463000)
1 引 言
泥石流是我国山区最为常见的地质灾害之一,具有突发性、流速快、流量大、物质容量大和破坏力强等特点。发生泥石流常常会冲毁公路铁路等交通设施甚至村镇等,造成巨大损失。因此,在灾前评价泥石流的危险程度,定量给出其危险度估计值就显得非常重要,对于减轻泥石流可能造成的生命财产损失具有重要的意义。泥石流危险度是指在人类及所在环境中的一切事物遭受泥石流损害的可能性大小[1]。其评价研究一直是国内外泥石流研究的一个重要课题。我国最早对单沟泥石流危险度的评价研究以刘希林的“泥石流危险度判定的研究”为代表,给出了基于灰关联分析的泥石流危险度评价的因子选择和权重确定方法,危险因子采用等级赋值或者公式化赋值[2-6]。随后,国内学者在此基础上,进一步将集对分析、模糊数学、神经网络、信息熵等非线性科学理论应用到泥石流危险度评价中[7-10]。在这些方法中,评价因子的选取和权重的确定仍是其中最为关键的问题。
理论上,泥石流危险度是泥石流规模——频率曲线的定积分[6],而现实中泥石流规模和频率难以直接确定,因此,目前泥石流危险度评价通常采用以泥石流的规模和频率作为主要因子,以泥石流所在流域的岩石构造、地形地貌、水文气象、植被土壤和人类活动等条件作为次要因子的多因子综合定量评价模型[6]。对于单沟泥石流危险度评价,两个主要危险因子是必不可少的,而可供选择的次要危险因子较多。对于不同区域,泥石流沟发育的关键危险因子各不相同,每个危险因子对评价结果的贡献也不同,因此,需要对危险因子进行合理的筛选,以简化多因子评价体系,同时满足评价精度的要求。现有选取泥石流危险因子的方法主要有关联度法、投踪寻影法、相关系数法等[11],其中以刘希林采用的双系列灰色关联度分析最为经典,其以泥石流规模和发生频率为主要内在因子,采用灰关联分析计算次要危险因子与主要危险因子的关联度,从而提取关键的次要危险因子[2]。但这些方法在筛选次要危险因子时并未考虑各因子之间的单调性差异以及主、次危险因子之间的非线性关系,使得评价结果并不一定准确。为此,本文采用散点图结合Spearman等级相关[12]评价泥石流主、次危险因子之间的相关性,作为泥石流危险因子筛选的依据,采用Spearman等级相关系数计算各因子的权重,利用云南省37条泥石流沟的基础数据[2],建立泥石流危险度综合评价模型。该方法尽可能避免危险因子的单调性和非线性对评价结果的影响,突出了物源条件和动力条件对泥石流危险性的贡献。
2 泥石流次要危险因子的筛选
我国泥石流危险度的评价研究以刘希林的“单沟泥石流危险度计算”为代表。其主要经历了3个发展阶段[5],但指标体系的构建基础都是 2个主要因子和14个次要因子。这也是本文因子筛选的基础。
(1)主要因子:一次泥石流最大冲出量 M(104m3)(表示泥石流规模)、泥石流发生频率 F(%)。
(2)次要因子:流域面积S1(km2)、主沟长度S2(km)、流域最大相对高差S3(km)、主沟平均比降S4、形成区山坡坡度S5(°)、流域切割密度S6(km/km2)、主沟床弯曲系数 S7、松散固体物质储量S8(104m3)、泥砂补给段长度S9、24 h最大降雨量S10(mm)、年平均降雨量S11(mm)、植被覆盖率 S12(%)、垦殖指数 S13(%)、流域内人口密度S14(人/km2)。
2.1 次要危险因子的初步筛选
经典的泥石流危险度评价模型中,以灰关联分析进行次要危险因子的筛选,在进行灰关联分析时,未考虑因子之间的单调性差异。比如泥石流规模和频率对于泥石流危险性的贡献都是单调递增的,而植被覆盖率一般对于泥石流危险性的贡献是单调递减的,沟坡比降则是适中型指标,在适宜的范围内,泥石流危险性增大。同时,泥石流危险因子之间并非简单的线性关系,以相关系数进行因子筛选也存在一定的不足。为此,综合考虑以上各种因素的影响,本文采用散点图直观地表现出主、次危险因子之间的关系。采用云南省 37条泥石流沟的基础数据[2]。其中,一次泥石流最大冲出量数量级从0.1~102,泥石流发生频率数量级从1~103。由于幂律是自然界普遍存在的规律,根据两个主要危险因子的数量级分布特征,本文对其采用以10为基的对数坐标。次要危险因子根据情况分别采用对数坐标或者正常坐标。图1分别是一次泥石流最大冲出量与次要危险因子之间的关系图。
从图1可以看出,经过相应的坐标调整后,流域面积、主沟长度、流域最大相对高差、松散固体物质储量在对数坐标下与一次泥石流最大冲出量之间具有明显的正相关关系;流域切割密度、主沟床弯曲系数、泥沙补给段长度在正常坐标下与一次泥石流最大冲出量之间具有明显的正相关关系;而植被覆盖率在正常坐标下与一次泥石流最大冲出量之间具有明显的负相关关系。由此说明了这些次要危险因子与泥石流规模并非简单的线性关系。主沟平均比降、形成区山坡平均坡度、24 h最大降雨量、年平均降雨量、垦殖指数、流域内人口密度与一次泥石流最大冲出量之间没有明显的相关关系,说明这些次要因子不是该地区影响泥石流规模的关键因子,在初步筛选中予以剔除。
对于泥石流发生频率和次要危险因子之间的关系图与一次泥石流最大冲出量基本一致,仅流域面积结果不同,与泥石流发生频率不存在明显关系。其中主沟长度、流域最大相对高差、流域切割密度、主沟床弯曲系数、松散固体物质储量、泥沙补给段长度、植被覆盖率和泥石流发生频率之间具有明显的相关关系,其中植被覆盖率和泥石流发生频率是负相关,主沟长度、流域最大相对高差、松散固体物质储量在对数坐标下与泥石流发生频率具有正相关关系。由于篇幅有限,次要危险因子与泥石流发生频率的关系图并未一一列出。

图1 一次泥石流最大冲出量与各次要危险因子的关系图Fig.1 Scatter diagrams of the maximum quantity rushed out of a debris flow and secondary risk factors
2.2 次要危险因子的进一步筛选
从初步筛选结果可以得出,流域切割密度、主沟床弯曲系数等次要危险因子与主要危险因子之间存在明显的相关关系,但图中散点比较分散,需要进一步量化分析以筛选与主要危险因子具有显著关系的次要危险因子。由于泥石流主、次危险因子之间具有不同的非线性关系,次要危险因子的单调性存在差异,因此,简单的相关系数和灰关联分析都不适合筛选次要危险因子。为此,本文对泥石流危险因子进行等级划分,利用Spearman等级相关系数筛选次要危险因子,以避免因子之间的非线性和单调性差异对筛选结果的影响。
2.2.1 Spearman等级相关系数
Spearman相关系数又称为秩相关系数,是利用两变量的秩次大小作线性相关分析,对原始变量的分布不做要求,属于非参数统计方法,其适用范围比Pearson相关系数要广得多[12]。Spearman等级相关系数适用于测度两顺序变量的相关性。顺序变量的取值能够表示某种顺序关系。如泥石流危险因子的等级:1为无危险;2为极低危险;3为低度危险;4为中度危险;5为高度危险;6为极高危险。Spearman等级相关系数的计算公式为[12]

与简单相关系数类似,Spearman等级相关系数的取值区间[-1,1]。rs>0,两变量存在正的等级相关;rs<0,两变量存在负的等级相关;rs=1,表明两个变量的等级完全相同,存在完全正相关;rs=-1,表明两个变量的等级完全相反,存在完全负相关;rs=0,表明两个变量不相关。
由于 Spearman等级相关系数是一种非参数方法,只需将变量进行合理的等级划分就可以计算变量之间的相关性,最大程度上避免了因子之间的量纲、数量级、单调性以及非线性关系等对筛选结果的影响。泥石流主、次危险因子之间的 Spearman等级相关系数计算步骤如下:
(1)对泥石流危险因子进行等级划分,按等级次序编号;
(2)按顺序求出两个因子的每对等级编号的差;
(3)按式(1)计算等级相关系数。
2.2.2 基于Spearman等级相关系数的泥石流危险因子筛选
在计算 Spearman等级相关系数首先要对各危险因子进行等级划分。从云南省37条泥石流沟的基础数据[2]中可以发现,一次泥石流最大冲出量数量级从0.1~102,泥石流发生频率数量级从1~103,因此,对它们采用非等区间等级划分,在泥石流危险因子等级及赋值新表[2]中,已经采用了这种等级划分方法。至于次要危险因子,同样根据其数量级变化选择非等区间、等区间或者近似等区间等级划分形式。根据泥石流危险因子等级及赋值新表[2],除松散固体物质储量和植被覆盖率外,其余因子都可以按照该表进行等级划分。松散固体物质储量按照非等区间划分等级,植被覆盖率按照等区间划分等级。各危险因子等级划分标准如表1所示。

表1 泥石流危险因子等级及赋值Table 1 Grade and assignment of risk factors
以云南省 37条泥石流沟的基础数据[2]对各泥石流危险因子确定等级 1~6,然后计算 Spearman等级相关系数,结果如表2所示。
从表中的结果可以看出,Spearman等级相关系数计算结果与初步筛选结果是一致的。其中,一次泥石流最大冲出量与初步筛选的各项次要危险因子之间存在非常显著的相关关系(sig <0.01);泥石流发生频率与初步筛选的各项次要危险因子之间存在显著相关关系(sig <0.05)。为了进一步筛选重要危险因子,简化多因子计算体系,本文选取rs>0.5,sig <0.01作为次要危险因子筛选依据,从而得到了以下多因子评价体系(见图2)。
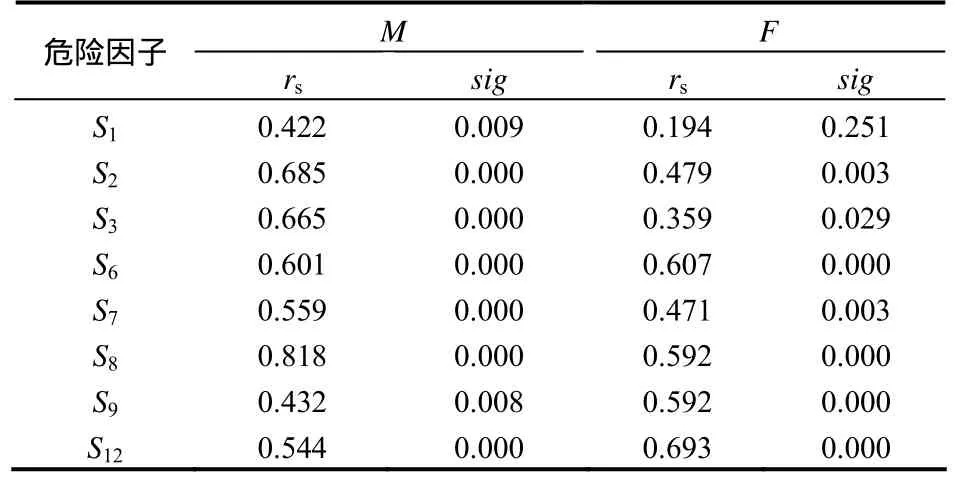
表2 主、次危险因子的Spearman等级相关系数与显著性Table 2 Spearman coefficients of rank correlations between the primary risk factors and secondary risk factors and their significance
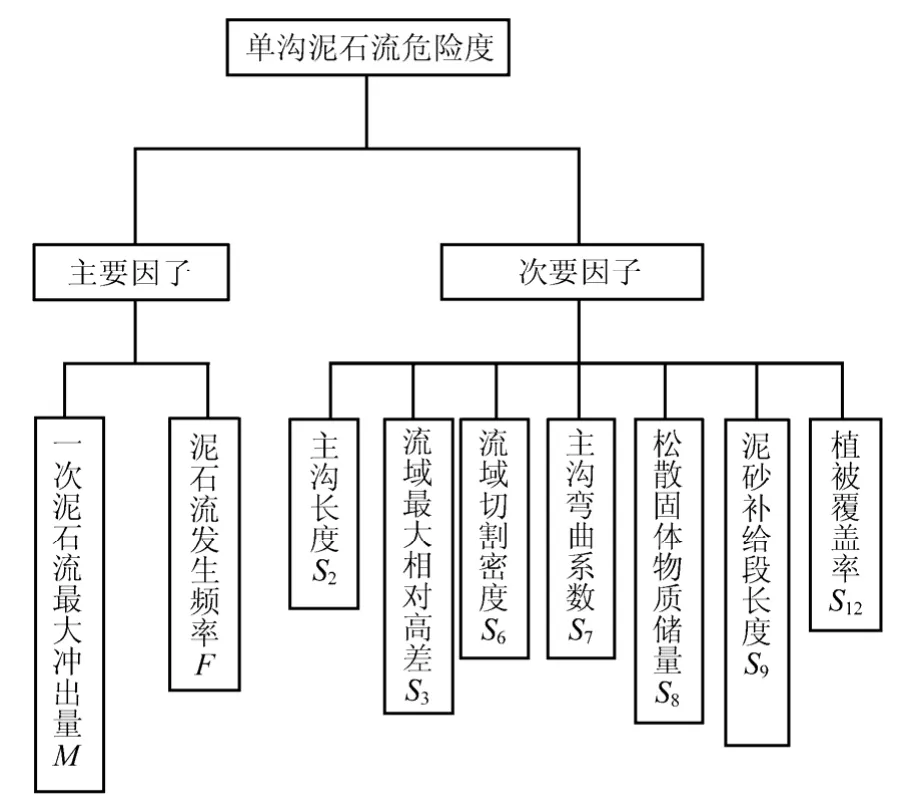
图2 泥石流危险度综合定量评价的因子体系Fig.2 Multiple factor system of comprehensive quantitative assessment of debris flow risk
对比双系列关联度分析的因子筛选结果[6]:流域面积S1、主沟长度S2、流域最大相对高差S3、流域切割密度S6、泥沙补给段长度S9。本文因子筛选中删除了流域面积S1,增加了主沟床弯曲系数S7、松散固体物质储量S8、植被覆盖率S12。泥石流的形成是地形条件、降雨条件和物源条件综合作用的结果,其中地形条件(主沟平均比降和形成区山坡平均坡度)和降雨条件(24 h最大降雨量和年平均降雨量)已经被删除,这是因为云南省这37条泥石流沟的主沟平均比降都在0.10以上,仅一条为0.09,形成区山坡平均坡度都大于 25°,满足泥石流发育的必要地形条件[13]。同时,云南省属印度洋季风气候区,绝大部分地区85%以上的降水集中在雨季,即使在干热河谷区,雨季 6~8月的总雨量也多在400 mm以上。这表明云南绝大部分地区雨季的降水已能满足泥石流的强烈活动对水分的要求[1]。因此,当地形条件和降雨条件这两个泥石流发育的必要条件已经具备时,泥石流的空间分布与活动(危险度)主要受控于物源条件。而本文最终筛选出来的这些因子,都是影响泥石流的物源条件以及动力条件的因子。松散固体物质储量S8和植被覆盖率S12更是影响泥石流的物质补给条件的重要因子,对泥石流的危险度评价具有重要影响,不可忽略。
3 泥石流次要危险因子权重确定
根据散点图以及Spearman等级相关系数,本文得到了以下危险因子的筛选结果。
(1)对泥石流规模具有重要影响的危险因子及其排序为:一次泥石流最大冲出量M >松散固体物质储量S8>主沟长度S2>流域最大相对高差S3>流域切割密度 S6>主沟床弯曲系数 S7>植被覆盖率S12。
(2)对泥石流爆发频率具有重要影响的危险因子及其排序为:泥石流发生频率F >植被覆盖率S12>流域切割密度S6>松散固体物质储量S8=泥沙补给段长度S9。
为了合理确定各危险因子的权重,本文从规模和频率两方面考虑。由于泥石流的危险度是规模和频率的共同作用,因此,分别对规模和频率赋予同样的权重0.5,再将0.5的权重对规模和频率的各自危险因子按等级相关系数进行比例分配。最后,如果次要危险因子对泥石流的规模和频率都有贡献,那么将其两方面的权重相加。分配结果如表 3~5所示。

表3 与泥石流规模相关的危险因子权重分配Table 3 Weight distribution of risk factors which are closely related to debris flow scale

表4 与泥石流频率相关的危险因子权重分配Table 4 Weight distribution of risk factors which are closely related to debris flow frequency

表5 危险因子权重分配Table 5 Weight distribution of risk factors
从表5的权重分配结果可以看出,植被覆盖率S12、流域切割密度S6、松散固体物质储量S8对泥石流的规模和频率都有贡献,因此,其权重分配超过了两个主要危险因子,说明次要危险因子在泥石流危险度评价中具有重要地位。而且这些次要危险因子都是泥石流的物源条件以及动力条件,对于泥石流的危险性影响重大,一旦泥石流活动加剧,良好的物源条件以及动力条件会进一步加大泥石流的危险性。
4 泥石流危险度综合评价模型与应用
泥石流危险因子的赋值可以按照表1确定,权重根据表5确定,由此可以根据线性加权法计算泥石流危险度的综合评价值。

式中:Rd为泥石流危险度;Wn′为危险因子权重,下标 n′可以是 M、F、S2、S3、S6~S9、S12; Si′为危险因子赋值,i′为 2、3、6~9、12。
为了检验本文泥石流危险度综合评价模型的有效性,特选择云南东川地区 12条典型泥石流沟[2]作为检验对象,并与文献[2]中的评价结果进行比较。东川市12条泥石流的基础数据见表6。泥石流危险度评价结果见表7。

表6 东川市12条泥石流沟的基础数据[2]Table 6 Basic data of 12 debris flow gullies in Dongchuan city [2]

表7 东川市12条泥石流沟危险度评价结果Table 7 Risk evaluation results of 12 debris flow gullies in Dongchuan city
从表7的评价结果可以看出,本文的危险度评价值明显高于文献[2]中结果,仅蒋家沟、大桥河、因民沟3条泥石流沟除外。本文的泥石流危险等级评价结果中有5条泥石流沟危险等级高于文献[2]中评价结果,其余与文献[2]中结果相同。其中文献[2]中已经指出达德沟和黑沙沟评价结果偏低,而本文评价等级高于文献[2]中结果,说明了本文结果更为可靠。对比其他的3条泥石流沟,其典型灾害、危害现状及活动趋势如表8所示。

表8 3条泥石流沟的典型灾害、危害现状及活动趋势Table 8 Typical disasters, damage status and activity trends of three debris flow gullies
从表8中可以看出,黑水河、深沟是中等规模的稀性泥石流沟,曾经造成过巨大损失,潜在危险性较大,而小白泥沟的目前的频率和规模都比较大,未来还存在进一步增强的可能,因此,本文对这 3条泥石流沟的危险等级更高是较为合理的。这也说明,在危险度评价模型中,强调物源条件和动力条件的作用,可以更好地估算泥石流的危险性。
5 结 论
(1)经典泥石流危险度综合评价模型在筛选次要危险因子时未考虑各因子之间的单调性差异以及主、次危险因子之间的非线性关系,本文以散点图的形式直观地给出了主、次危险因子之间的相关关系,作为次要危险因子初步筛选的依据。在此基础上以 Spearman等级相关系数进行了次要危险因子的进一步筛选,建立了泥石流危险度评价的多因子体系。
(2)以 Spearman等级相关系数对泥石流危险因子进行权重分配,建立了泥石流危险度综合评价模型。该评价模型充分考虑了物源条件与动力条件对泥石流危险度的贡献,得出的结论较文献[2]中的经典方法更加符合实际情况,可为今后的泥石流危险度研究提供参考。
(3)由于本文的泥石流危险度综合模型是以云南省37条泥石流沟的基础数据为依据建立的,适用于云南等西南山区泥石流危险度评价。由于不同地区的泥石流次要危险因子对危险度的贡献作用不同,在推广到其他地区时,还应考虑地区之间泥石流发育条件的差异性。
[1]朱静. 泥石流沟判别与危险度评价研究[J]. 干旱区地理, 1995, 18(3): 63-71.
[2]刘希林, 唐川. 泥石流危险性评价[M]. 北京: 科学出版社, 1995.
[3]刘希林. 泥石流危险度判定的研究[J]. 灾害学, 1988,3(3): 10-15.
[4]刘希林, 唐川, 张松林. 中国山区沟谷泥石流危险度的定量判定法[J]. 灾害学, 1993, 8(2): 1-7.LIU Xi-lin, TANG Chuan, ZHANG Song-lin.Quantitative judgment on the debris flow risk degree[J].Journal of Catastrophology, 1993, 8(2): 1-7.
[5]刘希林. 我国泥石流危险度评价研究:回顾与展望[J].自然灾害学报, 2002, 11(4): 1-8.LIU Xi-lin. Debris flow hazard assessment in China: a review and perspective[J]. Journal of Natural Disasters,2002, 11(4): 1-8.
[6]刘希林. 沟谷泥石流危险度计算公式的由来及其应用实例[J]. 防灾减震工程学报, 2010, 30(3): 241-245.LIU Xi-lin. Quantitative assessment on site-specific debris flow hazard and application[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010,30(3): 241-245.
[7]汪明武, 李丽, 金菊良. 泥石流危险度的改进集对分析模型[J]. 自然灾害学报, 2009, 18(6): 124-128.WANG Ming-wu, LI Li, JIN Ju-liang. An improved set pair analysis model for evaluation of dangerous degree of debris flow[J]. Journal of Natural Disasters, 2009,18(6): 124-128.
[8]王子健, 肖盛燮, 戴廷利, 等. 泥石流危险度模糊综合评判方法及应用[J]. 重庆交通大学学报(自然科学版),2008, 27(5): 794-798.WANG Zi-jian, XIAO Sheng-xie, DAI Ting-li, et al.Fuzzy comprehensive evaluation method and its application in judging the risk degree of debris flows[J].Journal of Chongqing Jiaotong University (Natural Science), 2008, 27(5): 794-798.
[9]刘涌江, 胡厚田, 白志勇. 泥石流危险度评价的神经网络法[J]. 地质与勘探, 2001, 37(2): 84-87.LIU Yong-jiang, HU Hou-tian, BAI Zhi-yong. Artificial neural network method for evaluating the dangerous degree of debris flows[J]. Geology and Prospecting,2001, 37(2): 84-87.
[10]张晨, 王清, 陈剑平, 等. 金沙江流域泥石流的组合赋权法危险度评价[J]. 岩土力学, 2011, 32(3): 831-836.ZHANG Chen, WANG Qing, CHEN Jian-ping, et al.Evaluation of debris flow risk in Jinsha River based on combined weight process[J]. Rock and Soil Mechanics,2011, 32(3): 831-836.
[11]孟凡奇, 李广杰, 李明, 等. 逐步判别分析法在筛选泥石流评价因子中的应用[J]. 岩土力学, 2010, 31(9):2925-2929.MENG Fan-qi, LI Guang-jie, LI Ming, et al. Application of stepwise discriminant analysis to screening evaluation factors of debris flow[J]. Rock and Soil Mechanics,2010, 31(9): 2925-2929.
[12]汪冬华. 多元统计分析与SPSS应用[M]. 上海: 华东理工大学出版社, 2010.
[13]陈宁生, 等. 泥石流勘察技术[M]. 北京: 科学出版社,2011.

