二维Frenkel-Kontorova模型中六角对称结构的摩擦现象*

贾汝娟 王苍龙 杨阳 苟学强 陈建敏 段文山3)†

2)(中国科学院兰州化学物理研究所,固体润滑国家重点实验室,兰州 730000)

3)(甘肃省原子分子物理与功能材料重点实验室,兰州 730070)

(2012年10月7日收到;2012年11月5日收到修改稿)

1 引言

凝聚态物理中有许多非线性现象都可以用一个处于周期外势的原子链来描述,这就是著名的Frenkel-Kontorova(FK)模型[1].FK模型在研究非平衡性质及其他物理领域,特别是在凝聚态物理中被广泛应用,如在超导体中的旋涡晶格[2,3]、电荷密度波(CDW)[4]、胶体[5]、热传导[6,7]、公度-不公度(CI)相变[8-10]等等,尤其是对固体摩擦现象[11-13].FK模型越来越多地受到研究者们的关注,因为它作为深入研究纳米摩擦学领域复杂问题的一种理论工具[14],可以使人们更容易理解纳米摩擦学的机理[15,16].虽然目前有许多一维FK模型的理论研究[17-21],但真实的物理系统并没有这么简单,所以将一维FK模型推广到二维FK模型很有必要.

近几年,在纳米摩擦学的研究中,从相互接触的两层原子间摩擦力的观测中可知,错合角对摩擦力有着明显的影响,对于一定大小的错合角,可以产生超润滑[9,22,23].这些结果和超导电性[24-27]中发现的结果相似,这就促使了进一步的理论研究,对摩擦力产生的微观机理的认识,对生物医学和工程材料的巧妙设计具有理论指导作用[21,28,29].

基于以上提到的理论[30]和实验[31,32]研究,我们讨论了二维FK模型,基底势采用周期性六角对称结构,系统从locked到sliding态的相变.运用分子动力学模拟方法[33,34],可以得到,随着外驱动力的增加,在某一临界力处,系统开始运动,原子的运动方向和外驱动力的方向不同.随着外驱动力的进一步增加,在另一临界力处,原子开始在外驱动力的方向上运动.我们将这两个临界力分别定义为最大静摩擦力和动摩擦力,为了更清楚地研究这两个力的特征,我们讨论了系统中外驱动力的大小和方向、势垒高度的大小、上层原子间的耦合系数,尤其是错合角θ对这两个临界力的影响.

2 模型

二维FK模型由上下两层原子层组成,上层原子采用六角对称结构,在外驱动力作用下,任意一个原子不仅受到最近邻6个粒子的作用,而且还受到下层二维周期性垫底势的作用.模拟中,基底势函数采用近似的六角对称结构：

其中,f为势函数的势垒高度,b为基底势x方向的周期.上下两层间的错合角为θ,因此垫底势可改写为

上层原子中的任意一个原子(n,m),它受到最近邻6个原子的作用,原子之间的相互作用势采用简单的简谐形式：(yi,j-yn,m-a)2],其中,K为耦合系数,a为上层原子间的平衡距离,任意原子(n,m)的位置可表示为(xn,m,yn,m),它的位移矢量rn,m(xn,m,yn,m)满足运动学方程：

式中,Fext=(Fextcosα,Fextsinα)是外驱动力,α为外驱动力Fext与x轴之间的夹角,γ为黏性阻尼系数.模拟中,为了计算方便,对运动方程(3)进行无量纲化处理,并设每个原子的质量Mn,m=1,b=1,f=0.01,K=1,γ=0.1.

在数值模拟中,我们采用四阶龙格-库塔法求解运动方程(3),初始时刻所有原子处在能量的最低点,外力Fext在绝热条件下逐渐增大,且对于每个Fext值都要给一个足够长的弛豫时间使系统达到一个稳定的状态.

3 数值结果及其分析

3.1 摩擦力(Fs和Fc)与外驱动力Fext的关系

图1描述了上层原子的平均速度¯υ随外驱动力Fext的变化曲线,初始时刻上层的每个原子均匀地分布在下层周期势阱底,在外驱动力的作用下,上层原子的平均速度逐渐地增大,系统从locked态到sliding态的过程中会产生一个临界力,当外驱动力小于这个临界力时,上层原子的平均速度为零,此时系统处于静止状态.反之,当外驱动力大于该临界力时,系统会产生相对运动.我们称该临界力为系统的最大静摩擦力Fs(简称静摩擦力),由于外驱动力沿着不同的方向α作用到原子上时,系统受到的静摩擦力Fs的大小也不同,所以系统的静摩擦力Fs会受到外驱动力方向的影响.β为原子的平均速度与x轴之间的夹角,把上层原子的平均速度方向与外驱动力的方向相同时对应的外驱动力的值定义为动摩擦力Fc,即α的变化从α/=β到α=β时的外驱动力的值.其中,Fc也受到外驱动力的方向α的影响.

图1 上层原子的平均速度随外驱动力的变化曲线 模型参数：f=0.01,K=1,θ=0°

图2 所示为Fs和Fc受外驱动力方向α的影响,当θ=0°时,曲线Fs和Fc关于α=60°对称,这与我们选择的基底势函数的形状有关.根据图2所示,我们把参数空间分为三个不同的区域：

1)区域AA(arbitrary angle)Fext＜Fs,系统的平均速度¯υ=0;

2)区域 CA(constant angle)Fs＜Fext＜Fc,β/=α;

3)区域SA(same angle)Fext＞Fc,β=α.

在区域AA(¯υ=0)中,上层系统处于静止状态.在区域CA中,¯υ的值不为零,系统开始运动,但运动方向和外驱动力的方向不相同.同时,静摩擦力 Fs关于α=60°对称,并且在α=0°,α=60°,α=120°处达到了最大值,然而在α=30°和α=90°处Fs有最小值.

当θ=0°时,Fc随α的变化分别在α=25°,α=35°,α=85°和α=95°处有四个相同的峰值,在α=30°和α=90°处,Fc有最小值,Fc也关于α=60°对称.所以在区域CA中,Fs和Fc受α的影响呈现出周期性的变化,数值模拟结果表明,静摩擦力周期性的变化与模型中采用的基底势函数的结构有关,即六角对称结构.在区域SA,β=α,原子的运动方向和外驱动力的方向相同.

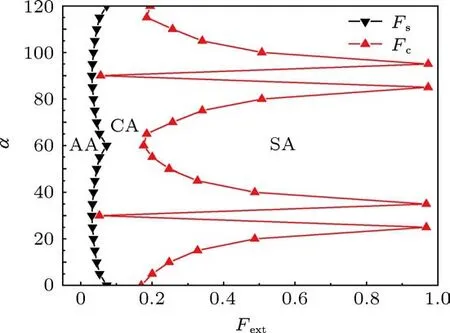
图2 Fs和Fc依赖于外驱动力的大小和方向 在 f=0.01,K=1,θ=0°;在区域AA,系统的平均速度为零;在区域CA,β/=α;在区域SA,β=α

图3 Fs和Fc依赖于外驱动力的大小和方向 在 f=0.01,K=1,θ=30°;在区域AA,系统的平均速度为零;在区域CA,β/=α;在区域SA,β=α

对于θ=30°的特殊情况,如图3所示.与图2相比,也有三个区域：AA,CA和SA,分别与Fext＜Fs,Fs＜Fext＜Fc和Fext＞Fc相对应.随着α的变化,在 α=55°,α=65°和 α=115°处,Fc有三个相同的峰值;在 α=0°,α=60°,α=120°处,Fc有最小值,但不再关于α=60°对称.而Fs在θ/=0°比θ=0°时的值小,几乎为零,不随α的变化而变化.因此,这两种临界力也依赖于错合角θ.

3.2 摩擦力(Fs和Fc)与错合角θ的关系

临界力Fs和Fc随着外驱动力的大小和错合角θ的变化见图4.根据图2我们可以划分为三个区域AA,CA和SA,分别对应于Fext＜Fs,Fs＜Fext＜Fc和Fext＞Fc.

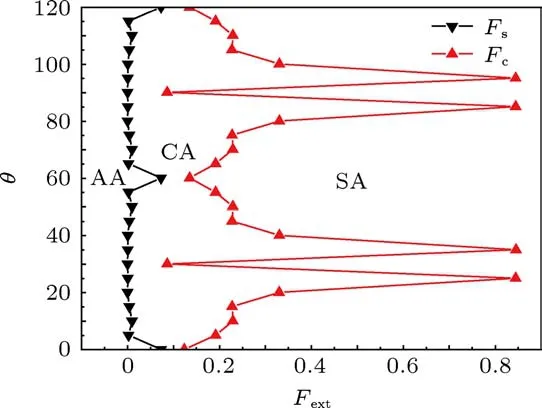
图4 Fs和Fc依赖于错合角θ,f=0.01,K=1,α=0°

在区域AA,原子的平均速度为零.在区域CA中,原子的平均速度为有限的值,但是原子的运动方向和外驱动力的方向不同.在θ=0°,60°,120°时处,Fs有最大值,且关于θ=60°对称.而在θ=30°,90°时,Fc有最小值,也关于θ=60°对称,同时,在θ=25°,35°,85°,95°时,Fc有四个几乎相等的峰值.在区域SA中,原子在外驱动力的方向上运动.从图4中可以看到,这两种临界力Fs和Fc明显地依赖于错合角θ.

图5 Fs和Fc依赖于错合角θ,f=0.01,K=1,α=30°

图5 中,对于α=30°的情况,与图4相比较,Fs和Fc随着θ的变化曲线不再关于θ=60°对称.随着θ值的变化,Fs和Fc的曲线呈现出周期性变化.显然α也对Fs和Fc有影响.

从以上的比较分析中,可以得到,Fs和Fc依赖于错合角θ的同时,α对Fc的影响也很大,进而Fs和Fc随着θ和α的变化而变化的情况比较复杂,这里我们只分析了α=0°,θ/=0°或α/=0°,θ=0°的情况.

3.3 摩擦力(Fs和Fc)与原子间的耦合系数K的关系

对于给定不同的θ和α的值,Fs和Fc依赖于原子的耦合系数K,见图6.

图 6(a)中,α=0°,θ=0°,Fs不受 K 的影响,但Fc明显地受到参数K的影响.此时有三个区域：AA,CA和SA.在区域AA内,原子几乎不动.在区域CA内,原子的运动方向和外驱动力的方向不同.在区域SA中,原子在外驱动力的方向上移动.图 6(b)中,α=10°,θ=0°时,Fs和 Fc的值也不相同,只有Fc依赖于耦合系数K,也有三个区域AA,CA和SA,分别与Fext＜Fs,Fs＜Fext＜Fc和Fext＞Fc相对应.在θ=0°时对于不同的α值,Fs的值几乎没有变化且不为零.对于θ/=0°,在图6(c)和图 6(d)中,分别为 α=0°,θ=10°和 α=10°,θ=10°.随着耦合系数K的增加,Fc的值的变化也很大.但是Fs的值变化很小,几乎为零,所以Fs与耦合系数K是相互独立的,即Fs不依赖于耦合系数K,在这种情况下,超润滑可能会产生.

图 6 Fs和 Fc随着耦合系数 K 的变化曲线 f=0.01;α,θ值：(a)α=0°,θ=0°;(b)α=10°,θ=0°;(c)α=0°,θ=10°;(d)α=10°,θ =10°

3.4 摩擦力(Fs和Fc)与势垒高度 f的关系

Fs和Fc随着势垒高度的变化曲线,如图7所示：(a)α=0°,θ=0°;(b)α=10°,θ=0°;(c)α=0°,θ=10°;(d)α=10°,θ=10°.在图 7(a)中,当外驱动力足够大时,可以看成有两个区域：AA和SA,此时,Fs=Fc.当 f继续增加时,Fs和Fc也随着增加.对于图7(b),(c),(d),我们可以看到有三个区域：AA,CA和SA且分别与Fext＜Fs,Fs＜Fext＜Fc,Fext＞Fc相对应.Fs和Fc也随着 f增加而增加.其中在图7(c)和图7(d)中,当θ/=0°时,静摩擦力很小,当 f接近于零时,静摩擦力也接近于零.

图 7 Fs和 Fc随着势垒高度 f的变化曲线 K=1;α,θ 值：(a)α=0°,θ=0°;(b)α=10°,θ=0°;(c)α=0°,θ=10°;(d)α=10°,θ =10°

根据以上的分析,我们要获得超润滑,必须采用势垒高度 f小的材料.同时,为了得到很小的摩擦力,必须选择合适的错合角θ.

4 结论

在具有六角晶格对称结构的二维FK模型中,我们研究了系统从locked态到sliding态的相变,数值模拟了具有六角晶格对称结构的摩擦行为.随着外驱动力的增加,在某一个临界值处,原子开始运动.随着外力的进一步增大,在另一临界力处,原子在外驱动力的方向上运动.把这两个临界力定义为两种不同的摩擦力,静摩擦力和动摩擦力,它们依赖于外驱动力的大小和方向,势垒高度,耦合系数和错合角.对于一定大小的错合角,摩擦力的值很小.特别是当错合角θ/=0°的情况,系统容易出现超润滑现象,我们将选择上层原子耦合系数较大和势垒高度较小的材料.同时,为了得到较小的摩擦力必须选择合适的错合角θ.

[1]Kontorova T A,Frenkel Y I 1938 Zh.Eksp.Teor.Fiz.8 1340

[2]Blatter G,Feigel’man M V,Geshkenbein V B,Larkin A I,Vinokur V M 1994 Rev.Mod.Phys.66 1125

[3]Marley A C,Higgins M J,Bhattacharya S 1995 Phys.Rev.Lett.74 3029

[4]Gr¨uner G 1988 Rev.Mod.Phys.60 1129

[5]Reichhardt C,Olson Reichhardt C J 2004 Phys.Rev.Lett.92 108301

[6]Hu B,Yang L 2005 Chaos 15 015119

[7]Shao Z G,Yang L,Zhong W R,He D H,Hu B 2008 Phys.Rev.E 78 061130

[8]Bak P 1982 Rep.Prog.Phys.45 587

[9]Yang Y,Wang C L,Duan W S,Shi Y R,Chen J M 2012 Acta Phys.Sin.61 130501(in Chinese)[杨阳,王苍龙,段文山,石玉仁,陈建敏2012物理学报61 130501]

[10]Li R T,Duan W S,Yang Y,Wang C L,Chen J M 2011 Euro.Phys.Lett.94 56003

[11]Xu Z M,Huang P 2006 Acta Phys.Sin.55 2427(in Chinese)[许中明,黄平2006物理学报 55 2427]

[12]Li X L,Liu F,Lin M M,Chen J M,Duan W S 2010 Acta Phys.Sin.59 2589(in Chinese)[李晓礼,刘锋,林麦麦,陈建敏,段文山2010物理学报 59 2589]

[13]Yang Y,Duan W S,Chen J M,Yang L,Teki´c J,Shao Z G,Wang C L 2010 Phys.Rev.E 82 051119

[14]Persson B N J 1999 Surf.Sci.Rep.33 83

[15]Qian L M,Luo J B,Wen S Z,Xiao X D 2000 Acta Phys.Sin.49 2240(in Chinese)[钱林茂,雒建斌,温诗铸,萧旭东2000物理学报49 2240]

[16]Wen S Z 1998 Nano Tnbology(Beijing：Tisinghua University Press)(in Chinese)[温诗铸1998纳米摩擦学(北京：清华大学出版社)]

[17]Zheng Z G 2001 Commun.Theor.Phys.36 37

[18]Hirano M 2003 Wear 254 932

[19]Xu H B,Wang G R,Chen S G 2000 Chin.Phys.9 0611

[20]Braun O M,Zhang H,Hu B,Teki´c J 2003 Phys.Rev.E 67 066602

[21]Li H X,Xu T,Wang C B,Chen J M,Zhou H D,Liu H W 2007 Tribol.Int.40 132

[22]Lin M M,Duan W S,Chen J M 2010 Chin.Phys.B 19 026201

[23]Wang C L,Duan W S,Hong X R,Chen J M 2008 Appl.Phys.Lett.93 153116

[24]Reichhardt C,Grønbech-Jensen N 2001 Phys.Rev.B 63 054510

[25]Reichhardt C,Zim´anyi G T,Grønbech-Jensen N 2001 Phys.Rev.B 64 014501

[26]Reichhardt C,Zim´anyi G T,Scalettar R T,Hoffmann A,Schuller I K 2001 Phys.Rev.B 64 052503

[27]Reichhardt C,Olson C J,Hastings M B 2002 Phys.Rev.Lett.89 024101

[28]Persson B N J,Albolu O,Tartaglino U,Volokitin A I,Tosatti E 2005 J.Phys.：Condens.Matter 17 R01

[29]Yang Y,Duan W S,Yang L,Chen J M,Lin M M 2011 Euro.Phys.Lett.93 16001

[30]Teki´c J,Braun O M,Hu B 2005 Phys.Rev.E 71 026104

[31]Yaron U,Gammel P L,Huse D A,Kleiman R N,Oglesby C S 1995 Nature 376 753

[32]Pardo F,de la Cruz F,Gammel P L,Bucher E,Bishop D J 1998 Nature 396 348

[33]Zhang Z H,Han K,Li H P,Tang G,Wu Y X,Wang H T,Bai L 2008 Acta Phys.Sin.57 3160(in Chinese)[张兆慧,韩奎,李海鹏,唐钢,吴玉喜,王洪涛,白磊2008物理学报 57 3160]

[34]Gong B Z,Zhang B J 2009 Acta Phys.Sin.58 1504(in Chinese)[龚博致,张秉坚2009物理学报58 1504]