声波在含气泡液体中的线性传播*
王勇 林书玉 张小丽
1 引言
声波在含气泡液体中的传播是一个非常复杂的现象,对线性小振幅状态和弱非线性状态下的声传播已有大量的研究,其中涉及温度、液体表面张力及液体的黏度等对声传播的影响.这方面最早的工作是1911年Mallock[1]关于液-气混合物中声传播问题的研究.van Wijngaarden[2]综述了关于小振幅弹性声波在含气泡液体中传播的多个方面的理论和实验研究,并对声传播过程中的非线性和损耗等现象进行了讨论.Caf l ish等[3,4]扩展了Wijngaarden的包括热传导和表面张力作用的理论.在线性近似下,可以用来计算气泡大小分散情况下线性振动时声波的衰减系数.Commander和Prosperetti[5,6]给出一种小振幅线性压力波在含气泡液体中传播的模型.他们指出气泡振动对线性声波衰减的影响通常较弱,除非当气泡的大小接近谐振尺寸、声场频率低于谐振频率、且在1%—2%的气泡体积含量的情况下,模型才比较有效.文献[7]在计入气泡声吸收作用的同时,就气泡空间分布的相关性对含气泡水介质中声传播特性的影响进行了讨论,指出当考虑含气泡水介质中气泡空间分布的相关性时,声衰减系数的峰值后移且其峰值较忽略此相关性时的峰值低平,随着气泡体积分数的增大,气泡空间分布的相关性增强,气泡的谐振频率增大、谐振时的声散射幅值减小.对于声波在含气泡液体中的非线性传播及对气泡产生的相关效应也有大量的研究[8-16].但存在于液体中的气泡会由于散射产生散射声场并和原始入射声场相互作用,改变入射声场的声压振幅,使其受气泡多少的影响.文献[17]指出入射声场应换为考虑到气泡作用时的等效入射声场.另外,对于气泡的振动过程,不能单一地认为是等温过程或绝热过程.本文利用Keller的气泡振动模型来描述气泡的振动,同时综合考虑气泡之间的声相互作用等来对线性声波在含气泡液体中的传播做进一步的研究.
2 含气泡液体的声学模型
本文中用平均的温度、声速、密度和压强描述这种含气泡液体,同时假设所有的气泡具有相同的大小并且在单位质量的混合物中有相同的气泡个数.声波在含气泡液体中的传播,用ρ,u,p分别表示液体密度、声速和压强.含气泡液体中的连续性方程可表示为
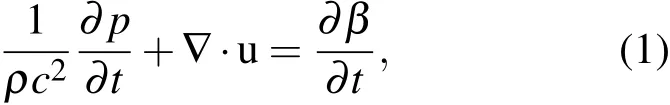
在方程(1)中,p表示声压场,u表示声速场,ρ和c分别表示纯液体的密度和声速,β表示气体所占的体积分数,表示如下

式中R表示气泡的瞬态半径,N表示液体中气泡的个数,根据我们建立的模型,在(2)式的时间微商中N必须保持常数,并且有β0=N4πR30/3.含气泡液体用声压场P和声速场u描述.考虑到动量方程的表示
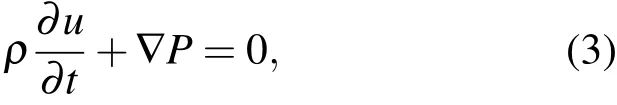
通过(1),(3)式可以得到:
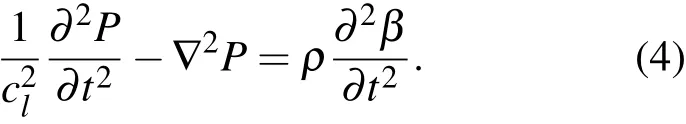
我们用(4)式来描述声波在含气泡液体中的声传播.当声波在纯液体中传播时上式右边等于0,则上式还原到纯液体中的声传播方程.
3 液体中的气泡模型
对于单个气泡的物理模型,我们做了几个假设:气泡保持球形;泡内气体是理想气体;泡内的压强空间分布均匀;忽略泡内包含的水汽;气泡的中心不动.考虑液体的黏滞作用和气液界面的热传导,忽略气泡的形成、破裂与合并等.在这些前提下气泡做径向的受迫振动,它的控制方程可以从气泡边界的压力连续方程中得到:
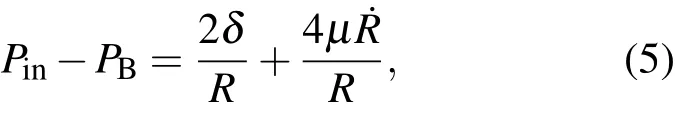
式中的圆点表示对时间的微分,PB表示气液边界液体侧的压强,常数µ表示周围液体的动态黏滞系数,P∞表示液体的环境压强,常数σ是气液界面的表面张力系数,Pin表示气泡内部的压强.从(5)式中可以很方便地得到:
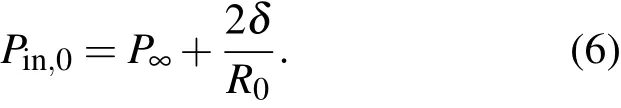
用Keller给出的在考虑液体压缩性时气泡的振动方程来描述气泡的振动
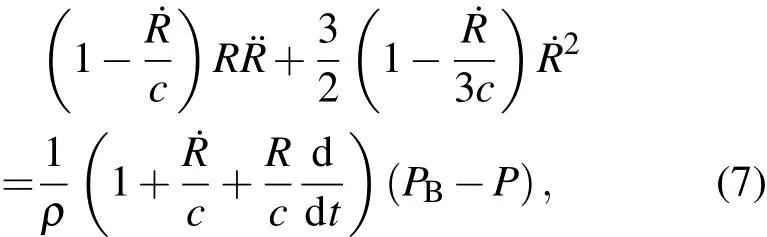
式中ρ,c分别表示液体密度及静态声速,P定义为气泡所在位置当气泡不存在时的压强[18,19],有

其中
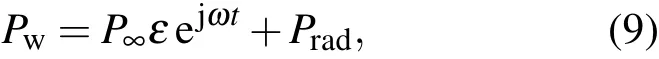
式中P∞表示液体静态压强,P∞εejωt表示驱动声场,Prad表示气泡的辐射声场.考虑到气泡之间的声相互作用时,根据文献[17]可得到驱动声场的等效入射声场
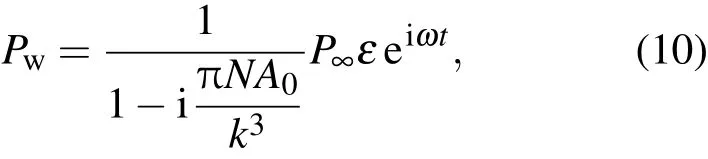
式中
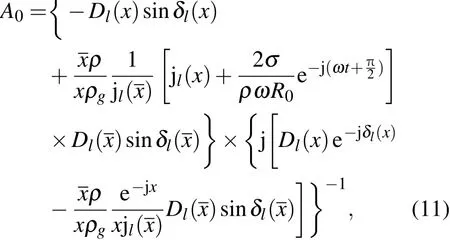
(11)式中x=kR0,x=kgR0,ρ0和ρ分别表示气泡内外介质的密度,k为波数,R0为气泡半径.Dl(x),δl(x)满足关系式
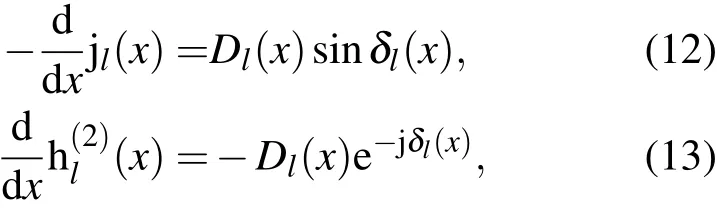
其中jl(x)与h(l2)(x)分别表示l阶的球贝塞尔函数和第二种l阶球汉开尔函数.
4 线性化求解
在ε≪1的情况下,驱动声场处于线性小振幅状态,我们认为声波在含气泡液体中线性传播,所以对于气泡来说它将在周期性声扰动下做小振幅振动.设

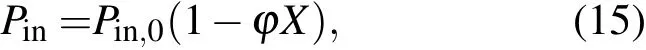
设X正比于 eiωt,式中

其中χ=D/ωR20,D为气体的热扩散系数[20].(15)式的引入考虑到了泡内气体和液体间的热相互作用,同时也认为气泡在振动过程中不是单一地做等温变化或绝热变化.X为和声场有相同的时间依赖性,于是有˙X=iωX,¨X=-ω2X,同时|X|认为和ε同阶[5,6,21,22].在≪1的情况下将(5),(6),(8),(14),(16)式代入(7)式并线性化得到:
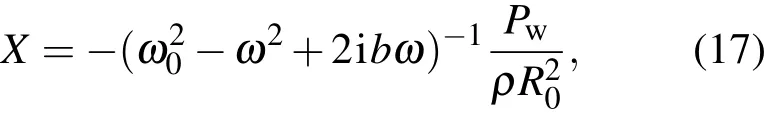
其中定义
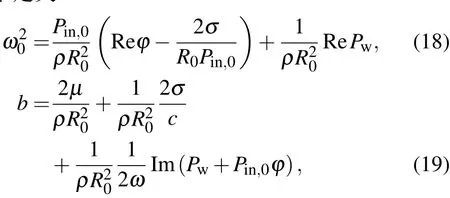
上式能明显表现气泡在线性声扰动时的谐振频率ω0和阻尼常数b,同时发现谐振频率和阻尼常数对于R0ω,φ和Pw均有依赖.对于谐振频率在(ωR0)/c≪1的情况下,气泡间的声相互作用会使谐振频率ω0的值增大,液体黏滞的作用对气泡谐振频率没有影响.(18)式在忽略气泡间声相互作用的情况下可以还原到Prosperetti[21]和Commander[20]的结论.方程(19)表示的阻尼系数显示能量耗散源于气液间的黏滞磨擦、气泡受液体表面张力的克服、声场辐射、热传导和气泡间的相互作用,后三者的作用通过φ和Pw体现,同时Pw的考虑会使黏滞系数b的值增大,像文献[17]指出的那样:泡之间的声相互作用等效于在每个气泡上附加了一项阻力从而使其阻尼增大很多.方程(17)式在忽略σ和Pw的情况下可以还原到Prosperetti等[6]的结论.将(8)式及(17)式代入波动方程(4)式中,得到
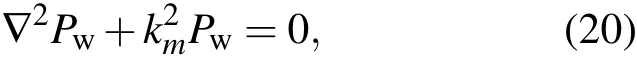
式中km表示含气泡液体的等效波数,有
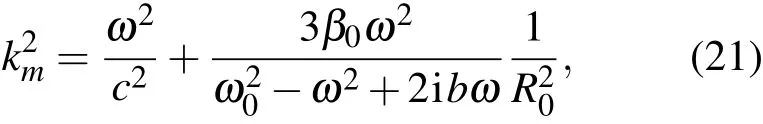
含气泡液体中的声速由

给出.由此可以看出,由于气泡在液体中的出现改变了液体中声传播的波数,使其等效于km,同时受β0,ω及R0的影响,从而影响到液体中声传播的速度.通过(21)式可以得到
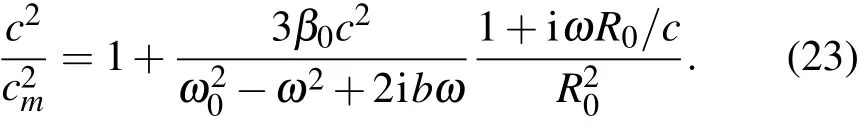
设

我们注意到有
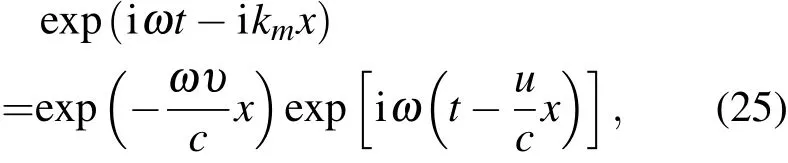
则衰减系数A可以表示为

出现在液体中的气泡会改变声波在液体中传播的声速及液体对声波传播的衰减系数.通过式(22)—(26)发现,含气泡液体中气泡的含量、大小及驱动声波频率均会对声波传播的速度和衰减产生直接影响,而气泡间的声相互作用及气泡与液体间热作用的影响则是通过谐振频率及阻尼系数间接体现的.
5 数值模拟
对声波传播过程中含气泡液体对声波的衰减系数和声波传播的速度进行了数值模拟.在数值模拟的过程中对一些参数的选取如下:P∞=1.01×105Pa,γ=1.4,D=2.4×10-5m2/s,µ=1.0042×10-3Pa/s,ε=0.001,σ=72.75×10-3N/m,ρ=998.203 kg/m3,ρg=1.1691 kg/m3,c=1500 m/s.由(26)式可知,声波在含气泡液体中线性传播时,气泡大小、多少和驱动声场频率均是含气泡液体对声波衰减的主要影响因素,所以我们模拟了这些因素对衰减系数的影响.在模拟的过程中我们确保满足(ωR0)/c≪1的关系,得到的结果如图1所示.如果控制气泡的大小和驱动声场的频率一定,会发现衰减系数随气泡体积分数的增加而增加.而对于相同体积分数的情况,气泡越小对应的衰减系数越大.由此可知在这种情况下,气泡的多少影响了混合液体的衰减系数.另外我们还模拟了衰减系数受驱动声场频率的影响,发现如果控制气泡体积分数和气泡大小不变,则衰减系数会随驱动声场频率的增加而增大.
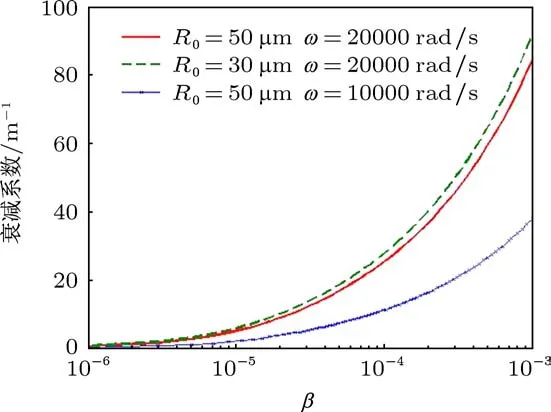
图1 气泡体积分数对声衰减系数的影响
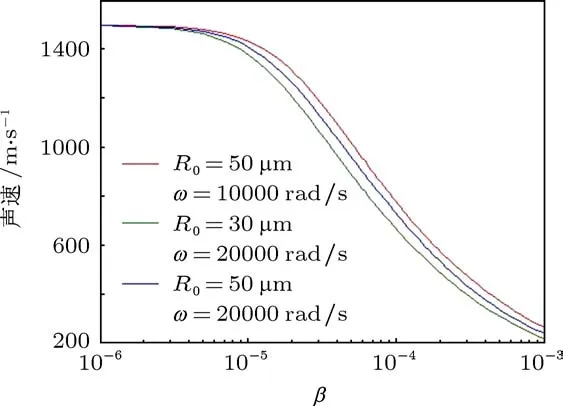
图2 气泡体积分数对声速的影响
对于含气泡液体中声传播的速度在其传播过程中受气泡体积分数的影响如图2所示.对于混合液体中的气泡来说,不管其大小如何,其体积分数的增加均会导致混合液体中声传播的速度减小,在体积分数和驱动声场频率相同的情况下,小气泡对应的声传播速度会小一些.对于气泡大小和体积分数均相同的情况下,驱动声波频率的增加会导致声传播速度的减小,但这一结论只能是在驱动声场频率远小于气泡的谐振频率的情况下适用.
6 结论
对于声波在含气泡液体中的线性传播,我们分别建立了含气泡液体的声传播模型和气泡的振动模型.在满足(ωR0)/c≪1的前提下,得到了气泡的谐振频率、阻尼常数、含气泡液体对声波传播的衰减系数和声传播的速度等的解析表达式.对于混合液体中的气泡,发现其谐振频率和阻尼常数均受气泡大小、气泡间的声相互作用、驱动声波频率及气泡与液体间热作用的影响.通过数值分析发现,气泡间的声相互作用虽然对气泡谐振频率和阻尼系数有影响,但对阻尼系数的影响不太明显.由于气泡在液体中的出现改变了液体中声传播的波数,所以使液体对声波在其中传播的参数发生变化.在驱动频率一定的情况下,气泡越小含量越多,声波传播的速度就会越小.驱动声波频率在远小于气泡谐振频率的情况下,声波传播速度会随驱动频率的增大而减小.气泡间的声相互作用对混合液体的衰减系数及声传播速度产生的影响不明显.所以认为气泡含量、大小和驱动声场频率是影响声波在含气泡液体中线性传播的主要因素.
[1]Mallock A 1911 Proc.R.Soc.Lond.A 84 391
[2]Wijngaarden L V 1972 Ann.Rev.Fluid Mech.4 369
[3]Caf l isch R E,Miksis M J,Papanicolaou G C,Ting L 1985 J.Fluid Mech.160 1
[4]Caf l isch R E,Miksis M J,Papanicolaou G C,Ting L 1985 J.Fluid Mech.153 259
[5]Commander K W,Prosperetti A 1989 J.Acoust.Soc.Am.85 732
[6]Prosperetti A,Crum L A,Commander K W 1988 J.Acoust.Soc.Am.83 502
[7]Li F X,Sun J C,Huang J Q 1998 J.Northwestern Polytech.Univ.16 241(in Chinese)[李福新,孙进才,黄景泉1998西北工业大学学报16 241]
[8]Kudryashov N A,Sinelshchikov D I 2010 Phys.Lett.A 374 2011
[9]Kudryashov N A,Sinelshchikov D I 2010 Appl.Math.Comput.217 414
[10]Vanhille C,Campos-Pozuelo C 2009 Ultrason.Sonochem.16 669
[11]Vanhille C,Campos-Pozuelo C 2011 Ultrason.Sonochem.18 679
[12]Louisnard O 2012 Ultrason.Sonochem.19 56
[13]Zhang J,Zeng X W,Chen D,Zhang Z F 2012 Acta Phys.Sin.61 184302(in Chinese)[张军,曾新吾,陈聃,张振福2012物理学报61 184302]
[14]Shen Z Z,Lin S Y 2011 Acta Phys.Sin.60 104302(in Chinese)[沈壮志,林书玉2011物理学报60 104302]
[15]Shen Z Z,Lin S Y 2011 Acta Phys.Sin.60 084302(in Chinese)[沈壮志,林书玉2011物理学报60 084302]
[16]Zhang P L,Lin S Y 2009 Acta Phys.Sin.58 7797(in Chinese)[张鹏利,林书玉2009物理学报58 7797]
[17]Qian Z W 1981 Acta Phys.Sin.30 442(in Chinese)[钱祖文1981物理学报30 442]
[18]Prosperetti A,Lezzi A 1986 J.Fluid Mech.168 457
[19]Foldy L L 1945 Phys.Rev.67 107
[20]Commander K W,Prosperetti A 1989 J.Acoust.Soc.Am.85 732
[21]Prosperetti A 1984 Ultrasonics 22 115
[22]Prosperetti A 1977 J.Acoust.Soc.Am.61 17

