不确定海洋声场中的检测性能损失环境敏感度度量*
刘宗伟 孙超 杜金燕
1 引言
真实的海洋环境由于受风浪、内波和海水中悬浮物等的影响,表现为一个时变和空变的复杂声传播信道.那些依赖于精确海洋环境参数的算法(包括最优检测算法和匹配场处理等)在实际应用中会遇到环境失配问题,其性能下降可能非常严重[1-3].因此一些学者以稳健信号处理为目标,取得了一系列的成果,有代表性的包括邻点约束最小方差波束形成器(MV NCL)[4]、环境扰动约束最小方差波束形成器(MV EPC)[5]、降维匹配场处理[6]、最优贝叶斯检测器(optimal uncertain fi eld processor,OUFP)[2,7,8]和估计海洋检测器(estimated ocean detector,EOD)[9-11]等.数据驱动的算法[12,13]不需要事先知道环境信息,也就不存在环境失配的问题,因此得到了广泛的关注.其一般的处理方法为首先根据阵列接收数据进行模态解卷,然后再利用解卷得到的模态进行后续的目标检测和定位等.也有学者研究了不确定度对后续信号处理的影响,包括:Balzo等[14],Tolstoy等[15],Schmidt等[4]和赵航芳等[16]分析了匹配场定位中的失配问题,其中赵航芳等定义了定位偏置、模糊度表面主瓣峰值比、主瓣背景比这3个量为性能度量,量化分析了宽带最小方差匹配场波束形成的性能对环境参量不确定性的敏感度;Kessel[17],Dosso等[18,19]和Pecknold等[20]研究了声场不确定对声传播幅度的影响,定义了声场传播敏感度函数,分别用线性、微弱线性和非线性的方法计算了敏感度,并得到结论:声传播中最敏感的几个参数(主要包括声速剖面和第一层底质参数)呈现非线性效应,而敏感度较弱的(主要包括除了第一层以外的其他底质参数)呈现线性效应.同时Pecknold等用2006浅海实验(shallow water experiment 2006,SW06)验证了环境参数的不确定对传播损失的影响.
研究海洋不确定声场对检测性能影响的工作并不多见.因此本文研究两者之间的关系,同时定义检测性能损失环境敏感度,为海洋声场不确定度评判和后续信号处理提供参考依据.敏感度的计算需要将声场环境的不确定传递到声信号空间中去.针对这个问题,目前主要包括两大类方法:一是解析类方法[17,21],二是使用蒙特卡罗方法[18].解析类方法直接将海洋环境参数的不确定性嵌入到波动方程中去,进而解算不确定声场,该类方法的优点是计算速度快,物理意义清晰,缺点是公式推导较为复杂,且往往局限于标准海洋环境.蒙特卡罗方法可以直接利用现有成熟的声场计算模型(包括简正波方法[22]、射线方法和抛物近似方法等)计算传播声场,结果可靠.其缺点是计算量较大,耗时长,但是随着硬件平台计算速度的提升和声场计算模型的优化,其耗时下降到一个可以负担的范围内.基于上述分析,本文使用蒙特卡罗方法结合声场传播计算模型分析检测性能损失敏感度.
检测性能损失环境敏感度反映了环境参数变动程度和检测性能损失之间的关系,可以认为是一个海洋环境不确定大小的固有物理描述量.现有的不确定度描述方法主要基于参数的概率密度函数(关键参数为方差)给出,不能真实反映对后续信号处理的影响.本文将参数的不确定度转化为信号检测性能损失环境敏感度,使得环境对信号处理的影响更加直观.
2 理论模型
2.1 声传播模型
设海水密度为ρ,由位于r0=(0,zs)的单频点声源激励,在r=(r,z)处产生的声场p(r)满足Helmholtz方程
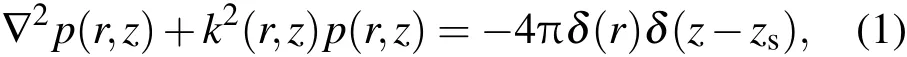
其中k(r,z)=ω/c(r,z),z取向下为正方向,ω为声源角频率.为了求解方程(1)现在已经形成了若干方法,包括简正波理论方法、射线理论方法、波数谱积分方法和抛物近似方法等[23].远场低频情况下简正波理论可以快速有效地求解辐射声场,在柱坐标下方程(1)的声场简正波表达式[23]
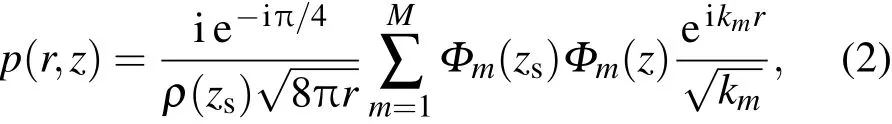
其中m表示模态号数,M表示当前声场环境中能够传播的最大简正波模式号数,本征函数Φm和本征值km分别表示第m号模式的形状函数和水平波数,Φm和km是声场参数(包括水中声速、海水深度和底质特性等)的函数.定义声场参数集为ψ,由(2)式可知,辐射声场p是ψ的函数.
按照通信理论,海洋环境可以看作水声传播信道,定义从声源到接收点的信道传递函数为G(ω,ψ).假设目标辐射信号为窄带信号,复幅度为a,中心频率为ω0,那么接收信号可以表示为aG(ω0,ψ).
2.2 确定海洋声场中的信号检测
考虑已知中心频率为ω0的窄带信号检测问题,建立如下模型
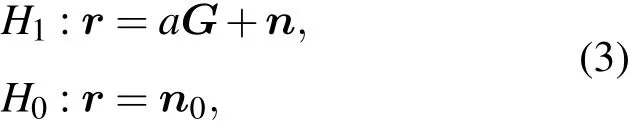
其中,r为 M×1列向量,对应于 M个空间分布的水听器,其值为每个水听器上接收数据时域快拍的窄带傅里叶变换;G=[G1(ω0,ψ),G2(ω0,ψ),···,GM(ω0,ψ)]T, 其 中Gi(ω0,ψ),i=1,2,···,M 表示从目标到第 i个水听器的信道传递函数[23];a是未知复数,表示未知的信号幅度与相位;噪声在频域由n0表示,为复高斯随机向量,且E(n0)=0,cov(n0)=2σ2nIN,表征了一个零均值方差为2σ2nIN的空间白噪声.
根据统计信号处理理论[24],可以得到两种假设下接收数据的概率密度函数为
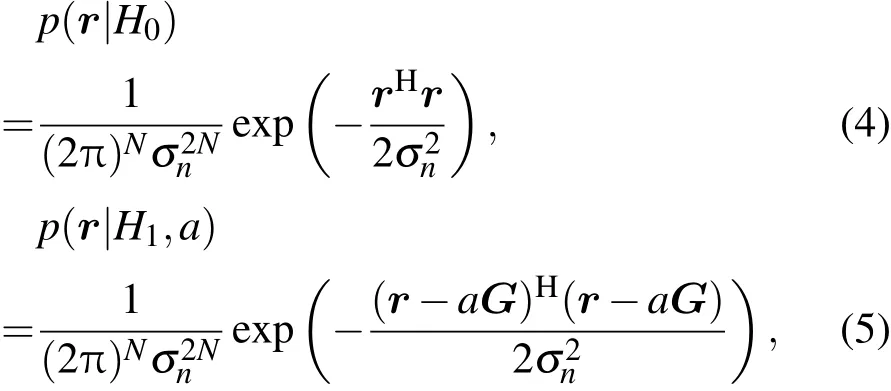
其中,p(r|H1,a)为条件概率密度函数,应用纽曼-皮尔逊(Neyman-Pearson,NP)方法得到条件似然比为
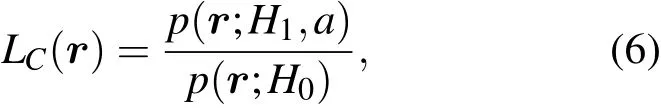
(6)式中a为未知参数,无法得到最终的检验统计量.解决的方法是使用广义似然比(generalized likelihood ratio test,GLRT)方法,也即使用a的最大似然估计量(maximum likelihood estimator,MLE)ˆa代替,
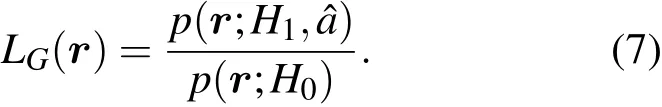
为了求ˆa,将(4)和(5)式代入(6)式并对其两边求对数,得到
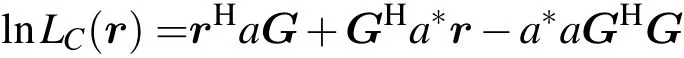

对(8)式两边求a∗的导数并令结果为0,得到a的MLE为

将(9)式代入(7)式,取对数并舍弃与数据无关项,得到最终检测统计量为
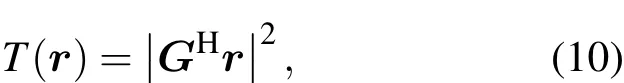
也即对于给定的检测门限γ,如果T(r)>γ判定目标出现,如果T(r)<γ判定没有目标.
2.3 不确定海洋声场环境中的检测性能损失敏感度
实际应用中,(10)式的声场传递函数由其估计值˜GH代替.由于环境参数的不确定导致接收声场不确定,最终使得˜GH往往不等于GH,如果接收声场函数的模相等,也即那么可得即由于环境失配必然导致检测性能的下降.其证明过程为:首先,两检测统计量差的期望为
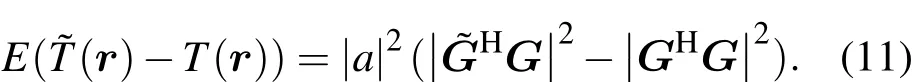
根据Cauchy-Schwarz不等式,
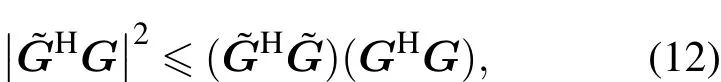
定义检测性能损失环境敏感度(environmental sensitivity in detection performance degradation,ESD)为
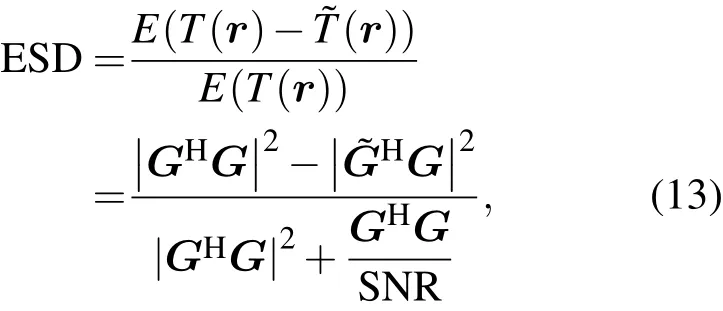
其中SNR=2σ2n/|a|2为目标处的信噪比,为了单独分析由于环境失配造成的检测性能损失,可以使信噪比无穷大,这时1/SNR∝0,可得
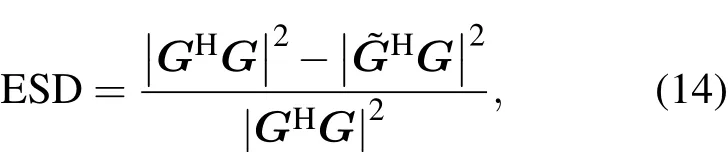
(14)式为环境参数确定失配情况下的敏感度计算方法,即环境参数有一个固定的偏移情况下检测性能损失.实际应用中这个固定的偏移一般无法得到,更为常见的是概率密度函数描述方法,也即环境参数由均值和方差表征,并且从属于一个概率密度函数,比如正态分布或者均匀分布.这时可以通过蒙特卡罗方法采样不确定环境参数,然后求平均得到环境随机失配情况下的敏感度计算方法:
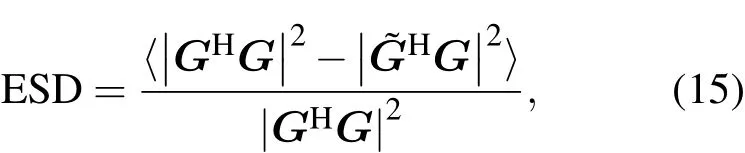
这里〈·〉表示蒙特卡罗采样上的整体平均.
ESD表征了各个环境参数不确定度和信号检测性能损失之间的关系,是一个广义上的环境物理描述量.有了该物理量可以更直观地对一个海域进行不确定度分析,同时为声场反演等问题提供参考.例如,如果一个物理量对信号检测性能损失影响很小,那么我们可以容忍该物理量较低的反演精度.
3 仿真实验及结果
本文采用地中海某处浅海海域作为计算案例来分析检测性能敏感度,这是一片研究较为深入并且比较典型的浅海海域,其海洋环境参数及其取值区间都可以获得,如图1所示.水中声速剖面在近海面处有一个较强的负梯度,并且在半水深处有一个微弱的声信道.3层海底介质由声速v1,v2,v3,密度ρ1,ρ2,ρ3和吸收系数α1,α2,α3表述,上面两层海底介质的深度分别为h1和h2.海洋环境参数的取值和不确定度在图1中给出,其中v0表征了因太阳照射和风浪引起的海面声速不确定,并且本文中假定其不确定度随着深度以指数衰减,到30 m水深时其不确定度为0,如图中虚线所示.声场计算模型基于简正波方法,以下分析中蒙特卡罗采样次数皆为300次.
假设声频率为750 Hz,分析20 km处环境敏感度随标准差变化的趋势,得到各个参数敏感度如图2所示,其值在0—130 m水深上进行了平均.可以看出检测性能整体上随着不确定度范围的增大而下降.其中环境参数v1,h1和v0的敏感度较高,同时随着标准差的增大,检测性能下降速度放缓.环境参数ρ2,α1和ρ1的敏感度较小且呈现较为强烈的线性特性.这个结果和Dosso等[18]的声场传播敏感度分析是符合的.
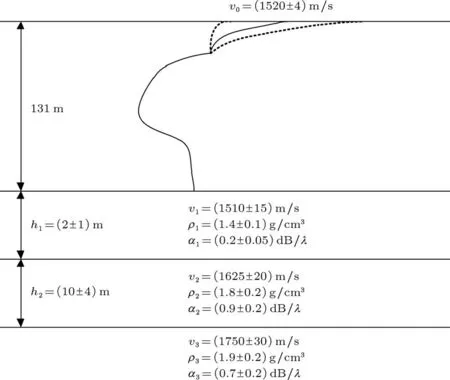
图1 海洋环境配置图,其中参数取值包括均值和标准差,参数都服从正态分布
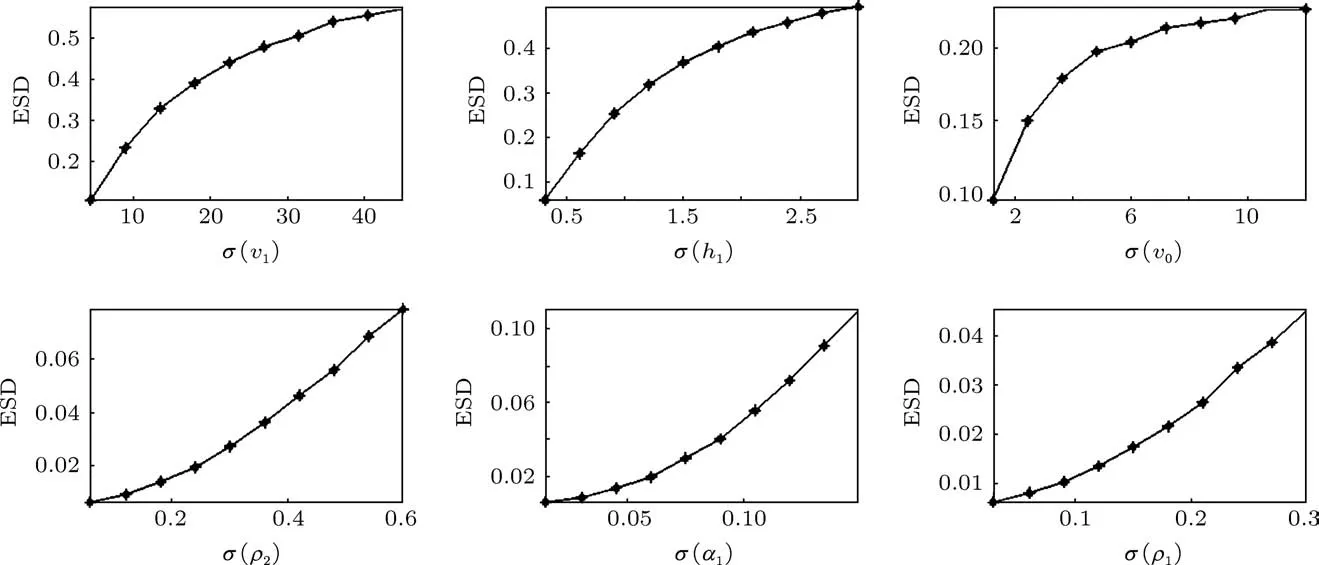
图2 不同环境参数的敏感度随标准差的变化情况
3.1 ESD的空间变化规律
假设声频率同样为750 Hz,分析距离100 m—20 km,深度5—130 m范围内因海洋环境不确定引起的检测性能损失.海洋环境参数假设为正态分布,其均值和标准差在图1中给出.图3所示为不同海洋环境下的检测性能损失敏感度,其中左边3幅图分别代表环境参数v1,h1和v0不确定时检测性能损失敏感度,其颜色取值范围0—0.6;相应的右边3幅图分别对应参数ρ2,α1和ρ1,其颜色取值范围为0—0.2.由图可知,第一层海底底质的声速v1对检测性能有较大的影响,并且随着距离有增大的趋势,在20 km处上层和下层水体中其检测性能敏感度为0.6,也就是说因为v1的不确定将损失60%的检测性能.h1对敏感度的影响集中在水体上层,且在近距离上取值也在0.4左右,这主要是由近场干涉效应引起的.v0的不确定带来上层水体中声速的波动,进而带来声传播的起伏,造成检测性能下降,其影响可由图中得到.上层水体中的检测性能下降非常严重,且随着距离增大而增大.ρ2,α1和ρ1对检测性能影响较小,且影响主要集中在近程.图3中6幅图的共同特点为:声轴附近检测性能损失较小,特别是在远距离上,这主要得益于声信号在声信道传播的稳定性.
图4给出了不同的环境参数敏感度随距离变化的关系,其中:图4(a)对应敏感度在水体深度为0—30 m上的平均,图4(b)对应30—100 m,图4(c)对应100—131 m.由图4可知,在上层水体介质中,由于海表面声速的不确定造成检测性能损失最为严重;出现声信道的中层水介质在检测中表现出稳定性,特别是在远距离上,各个参数的影响都在变小;在下层水介质中,其第一层海底底质声速v1是影响最大的.除了v1,h1和v0外的其他参数,对检测的影响主要集中在近距离范围内,且都随着距离增大而减小.
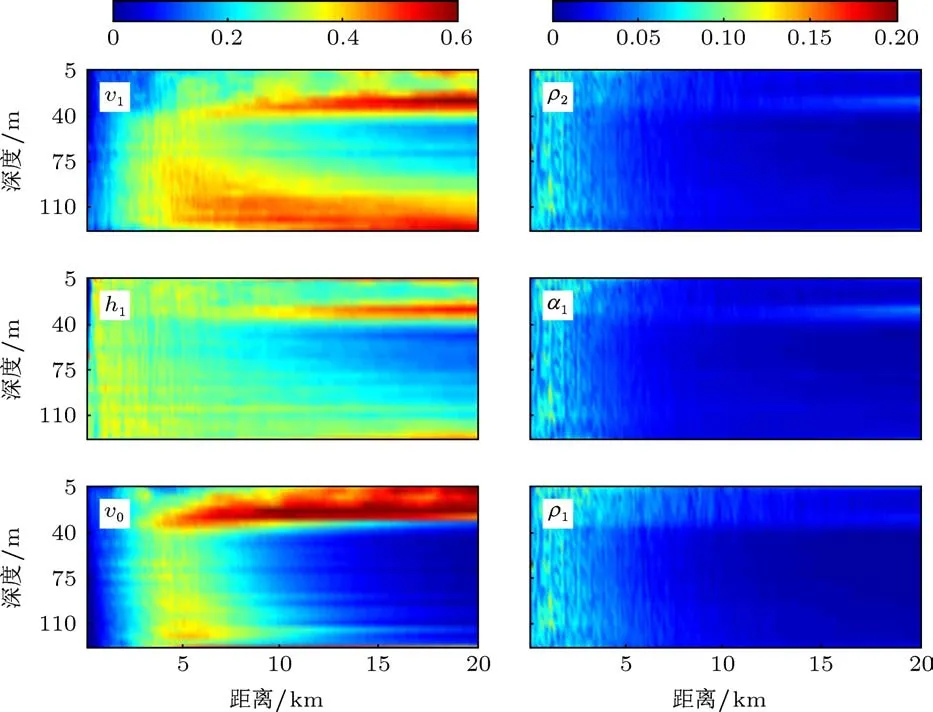
图3 不同海洋环境参数的检测性能损失敏感度空间变化特性
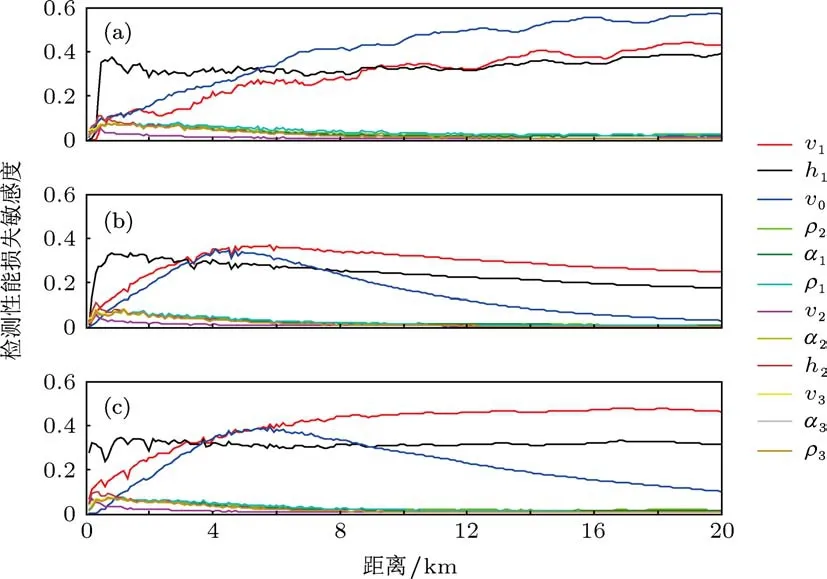
图4 不同深度下检测性能损失敏感度随距离变化图
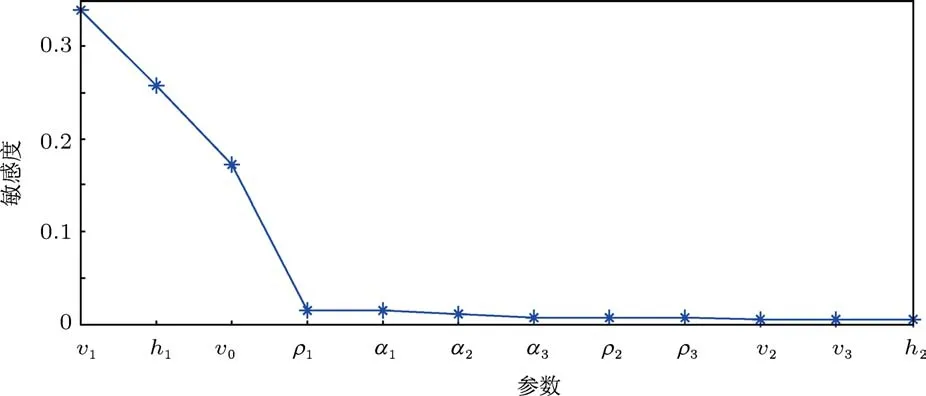
图5 各个环境参数的敏感度,20 km距离处
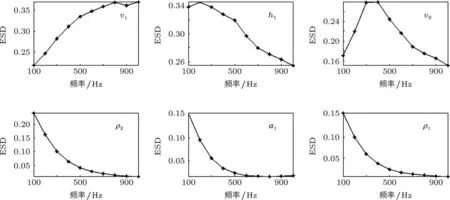
图6 环境敏感度随频率变化关系
在20 km处,把0—130 m水深的敏感度进行平均,得到如图5所示的各参数敏感度对比图.由图5可知,第一层海底底质的声速、厚度和水体中的声速剖面是对检测性能影响最显著的三个参数,而其他参数都影响较小.
3.2 ESD的频率变化规律
设定各个环境参数标准差大小为图1所示,声频率从100 Hz变化到1000 Hz,得到如图6所示的敏感度随频率变化趋势图.从图中可以看到第一层底质声速v1的敏感度随着频率升高而增大;海水表面声速的敏感度在频率300—400 Hz处达到最大值,随后随着频率的增大对检测性能的影响变小.底质参数h1,ρ2,α1和ρ1对检测性能的影响都随着频率升高而减小.
4 结论
本文定义了检测性能损失敏感度函数,并给出了在参数随机变动的情况下基于蒙特卡罗的计算方法.基于地中海某处海域的仿真计算表明:水体中声速剖面和第一层海底底质的声速和厚度是对检测性能影响最显著的量,其他环境参数对检测影响较小,且影响集中在近距离的检测上.这就使得我们在确定海洋环境参数时可以进行精度选择,对于对检测性能影响较大的量要保证其精度,而对于其他参数包括第二层和第三层底质的声速、密度和吸收系数等可以放宽精度要求.声轴附近的声信道中的检测性能是最稳定的,特别是在远距离上.不确定海洋声场中的信号检测和通信要利用声道轴的声场稳定传播效应.同时,参数敏感度还有较强的频率特性,第一层底质的声速对检测性能的影响随着频率升高而增大,底层介质厚度、密度和吸收系数等对检测的影响则随着频率升高而减小.
[1]Baggeroer A B,Kuperman W A,Mikhalevsky P N 1993 IEEE J.Ocean.Eng.18 401
[2]Pace N G,Jensen F B 2002 Impact of Littoral Environmental Variability of Acoustic Predictions and Sonar Performance(La Spezia,Italy:Kluwer Academic Publishers)p507
[3]Sha L W,Nolte L W 2005 J.Acoust.Soc.Am.117 1942
[4]Schmidt H,Baggeroer A B,Kuperman W A,Scheer E K 1990 J.Acoust.Soc.Am.88 1851
[5]Krolik J L 1992 J.Acoust.Soc.Am.92 1408
[6]Lee N,Zurk L M,Ward J 1999 Signals,Systems and Computers,1999 Conference Record of the Thirty-Third Asilomar Conference on Pacif i c Grove California,October 24—27,1999 p876
[7]Richardson A M,Nolte L W 1991 J.Acoust.Soc.Am.89 2280
[8]Shorey J A,Nolte L W,Krolik J L 1994 J.Comput.Acoust.2 285
[9]Sibul L H 2006 J.Acoust.Soc.Am.119 3342
[10]Culver R L,Camin H J 2008 J.Acoust.Soc.Am.124 3619
[11]Ballard J A,Culver R L 2009 IEEE J.Ocean.Eng.34 128
[12]Walker S C,Roux P,Kuperman W A 2005 J.Acoust.Soc.Am.118 1518
[13]Wang H Z,Wang N,Gao D Z 2011 Chin.Phys.Lett.28 114302
[14]Del Balzo D R,Feuillade C,Rowe M M 1988 J.Acoust.Soc.Am.83 2180
[15]Tolstoy A 1989 J.Acoust.Soc.Am.85 2394
[16]Zhao H F,Li J L,Gong X Y 2011 J.Harbin Eng.Univ.32 200(in Chinese)[赵航芳,李建龙,宫先仪2011哈尔滨工程大学学报32 200]
[17]Kessel R T 1999 J.Acoust.Soc.Am.105 122
[18]Dosso S E,Giles P M,Brooke G H,McCammon D F,Pecknold S,Hines P C 2007 J.Acoust.Soc.Am.121 42
[19]Dosso S E,Morley M G,Giles P M,Brooke G H,McCammon D F,Pecknold S,Hines P C 2007 J.Acoust.Soc.Am.122 2560
[20]Pecknold S P,Masui K W,Hines P C 2008 J.Acoust.Soc.Am.124 EL110
[21]Finette S 2005 J.Acoust.Soc.Am.117 997
[22]Porter M B 1991 The Kraken Normal Mode Program(La Spezia,Italy:SACLANT Underwater Acoustic Research Center)
[23]Jensen F B,Kuperman W A,Portor M B,Schmidt H 2000 Computational Ocean Acoustics(New York:American Institute of Physics)p67
[24]Kay S M 1993 Fundamentals of Statistical Signal Processing,Volume II:Detection Theory(Upper Saddle River,New Jersey:Prentice Hall)p34

