4Xn棋盘的染色计数问题分析
张上伟,吴 康
(华南师范大学数学科学学院,广东 广州 510631)
0 预备知识
为了方便讨论4Xn棋盘的染色计数问题,本文给出了以下三个引理:
引理1.1 设{an}n≥0和 {bn}n≥0是两个数列,s是非负整数,如果对任意的不小于s的整数n,都有,则对任意的不小于s的整数n,都有
引理1.2 以gm(n)表示用m(m≥2)种颜色去染2Xn棋盘,使得相邻格子异色的染色方法数,则gm(n)=m(m-1)(m2-3m+3)n-1.
以hm(n)表示用m(m≥3)种颜色去染3Xn棋盘,使得相邻格子异色且每一列格子中无相同颜色的染色方法数,则hm(n)=m(m-1)(m-2)[(m-1)(m-2)+(m-3)(m2-4m+5)]n-1.
引理1.3 以gm(n)表示m(m≥2)用种颜色去染2Xn棋盘,使得相邻格子异色,且每种颜色至少使用一次的染色方法数,则
以hm(n)表示用m(m≥3)种颜色去染3Xn棋盘,使得相邻格子异色,每一列格子中无相同颜色且每种颜色至少使用一次的染色方法数,则
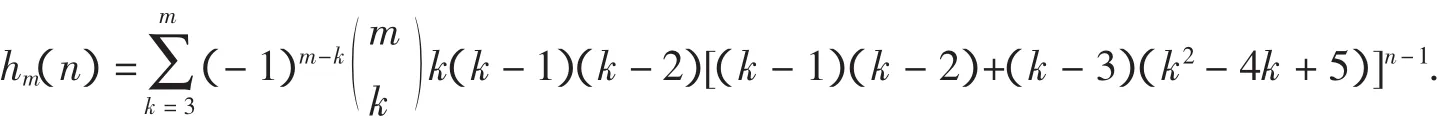
1 4Xn棋盘的染色计数问题分析
定理2.1 以fm(n)表示用m(m≥4)种颜色去染4Xn棋盘,使得相邻格子异色且每一列格子中无相同颜色的染色方法数,则

证明:利用加法原则和乘法原则证明计数公式.可分n个步骤,每个步骤对棋盘的一列格子进行染色.如图1.
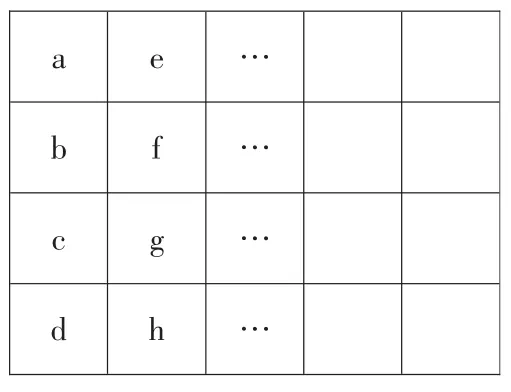
图1 4Xn棋盘
步骤1:对棋盘的第1列格子进行染色,因为相邻格子异色且每一列格子中无相同颜色,所以第1列格子的染色方法数为m(m-1)(m-2)(m-3).
步骤2:对棋盘的第2列格子进行染色,可分如下两类.
(一)e与b同色,属于此类的染色方法数可分为如下两类.
(1)f与c同色.属于此类的染色方法数可分为如下两类.
a)g与d同色.染色方法数为(m-3).
b)g与d异色.染色方法数为(m-3)(m-4).
(2)f与c异色.属于此类的染色方法数可分为如下三类.
a)f与d同色.染色方法数为(m-3)(m-3).
b)f与d异色且g与d同色.染色方法数为(m-3)(m-3).
c)f与d异色且g与d异色.染色方法数为(m-3)(m-4)(m-4).
(二)e与b异色,属于此类的染色方法数可分为如下两类.
(1)e与c同色.属于此类的染色方法数可分为如下三类.
a)f与d同色.染色方法数为(m-2)(m-3).
b)f与d异色且g与d同色.染色方法数为(m-3)(m-3).
c)f与d异色且g与d异色.染色方法数为(m-3)(m-3)(m-4)..
(2)e与c异色.属于此类的染色方法数可分为如下七类.
a)e与d同色且f与c同色.染色方法数为(m-2)(m-3).
b)e与d同色且f与c异色.染色方法数为(m-3)(m-3)(m-3).
c)e与d异色且f与c同色且g与d同色.染色方法数为(m-4)(m-3).
d)e与d异色且f与c同色且g与d异色.染色方法数为(m-4)(m-3)(m-4).
e)e与d异色且f与c异色且f与d同色.染色方法数为(m-4)(m-3)(m-3).
f)e与d异色且f与c异色且f与d异色且g与d同色.染色方法数为
(m-4)(m-4)(m-3).
g)e与d异色且f与c异色且f与d异色且g与d异色.染色方法数为
(m-4)(m-4)(m-4)(m-4).
由加法原则可知,第2列格子的染色方法数为以上染色方法数的总和,为
(m-3)(6m2-37m+61)+(m-4)4.
再考虑第3列直至第n列,其染色方法数与考虑第2列格子的染色方法数类同,每一列格子的染色方法数均为(m-3)(6m2-37m+61)+(m-4)4.
再根据乘法原则可知,fm(n)=m(m-1)(m-2)(m-3)[(m-3)(6m2-37m+61)+(m-4)4]n-1.
定理2.2以fm′(n)表示用m(m≥4)种颜色去染4Xn棋盘,使得相邻格子异色,每一列格子中无相同颜色且每种颜色至少使用一次的染色方法数,则

证明:由定理2.1知,用m(m≥4)种颜色去染4Xn棋盘,使得相邻格子异色且每一列格子中无相同颜色的染色方法数为

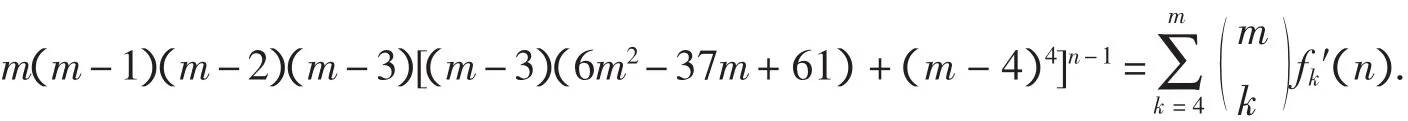
由引理1.3,可得
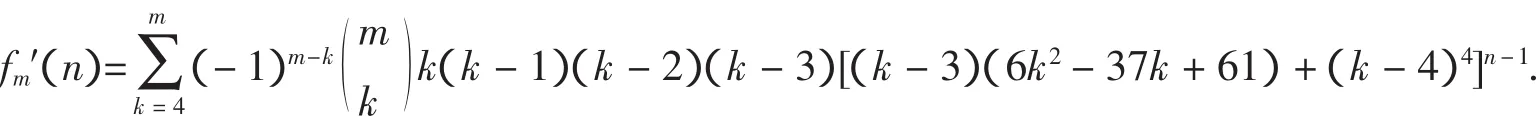
[1]曹汝成.组合数学[M].广州:华南理工大学出版社,2000.
[2]杨胜良.组合数学引论[M].兰州:兰州大学出版社,2006.
[3]顾红俏.关于棋盘的染色计数公式[J].新疆师范大学学报:自然科学版,2007(03):90-92.
[4]柳柏濂,吴康.竞赛数学的原理和方法[M].广州:广东高等教育出版社,2005.
[5]熊斌.棋盘的染色问题[J].中等数学,1991(01):25-28.

