基于泰勒级数法的边坡稳定性分析方法

潘 健,马 勇,高 珏

(华南理工大学土木与交通学院,广东 广州 510640)

0 引言

可靠度分析方法的引入对土木工程设计方法的革新起到了巨大的推动作用.特别是在结构设计领域,可靠度方法已形成了一套完整的基于概率理论的极限状态设计方法.然而,在岩土工程领域,特别是边坡工程领域,虽然有大量的学者投入到这方面的研究[1-5],但实际应用可靠度理论还是局限于少数特殊工程.

美国著名岩土工程师Duncan在其文章中指出:"制约可靠度理论在岩土工程中的应用主要有两点原因.其一,大多岩土工程师不熟悉可靠度理论的概念和模型;其二,人们常常误以为可靠度分析需要更多资料,会花费更多时间和精力[4]".为此本文尝试采用泰勒级数法这一简单的概率分析方法,将可靠度分析方法与传统的安全系数法结合起来,形成了一种简化的可靠度分析方法,并将其应用于边坡工程可靠度分析中.

1 泰勒级数法

泰勒级数法由美国土木工程师Wolff[3]首先提出,后来Duncan[4]又对其应用进行了一系列研究,最终形成了一套系统的、简便的、可靠的岩土工程可靠度分析方法.国内该方法的应用不多,作者曾尝试将该方法应用于地基沉降计算[6].

1.1 土坡稳定安全系数

我国现行规范通过土坡稳定安全系数描述土坡的可靠程度.针对不同的边坡类型,采用对应的安全系数计算公式.只要计算出来的安全系数大于目标安全系数,人们就认为土坡就是稳定的,这一过程可以归结为以下公式:

式中,K为安全系数;R为抗力;S为作用力;[K]为目标安全系数,可根据边坡工程安全等级和计算方法确定.

这一方法被称为安全系数法,又称单一安全系数法,将设计变量视为非随机变量,在强度上根据经验打一折扣作为安全储备.由于抗力和作用都是定值,所以安全系数也是定值,这种方法属于定值法.由于土性参数具有一定的不确定性,传统的安全系数法并不能恰当地考虑不确定性的影响,结果出现安全系数满足规范要求仍然发生边坡失稳的情况[4].可靠度理论是建立在概率统计基础上,以随机变量和随机过程为研究对象,它与定值分析方法最大区别是考虑了变量的随机性,并用严格的概率度量结构的安全度,就土坡稳定分析而言,可靠度理论是建立在土体具有的抗力大于荷载效应的概率基础上进行设计和校核的,因此更符合客观实际.可见在边坡工程设计中,引入可靠度分析方法是十分有必要的[17].

1.2算例

图1所示,某工程场地勘测地基土分为两层.第一层为粉质粘土,天然重度γ1=18.2 kN/m3,标准差 σγ1=0.91 kN/m3;内摩擦角φ1=23°,内摩擦系数(内摩擦角的正切值)f1=0.424,标准差σf1=0.036;黏聚力c1=5.8 kPa,标准差σc1=0.44 kPa;层厚h1=2.0 m.第二层为粘土,天然重度γ2=19.0 kN/m3,标准差σγ2=0.95 kN/m3;内摩擦角φ2=18°,内摩擦系数f2=0.325,标准差σf2=0.026;黏聚力c2=8.5 kPa,标准差σc2=0.64 kPa;层厚h2=8.3 m.基坑开挖深度5.0 m,基坑开挖边坡为1:1,不考虑地下水的作用.

图1 边坡算例示意图

(1)土坡稳定分析

整体稳定分析采用《建筑边坡工程技术规范》(GB50330-2002)推荐使用的圆弧滑动面法进行分析,则土坡稳定安全系数K公式为:

式中,φi为第i个土条的内摩擦角;n为土条的数目;Qi为第i个土条的自重;αi为第i个土条法向分力与垂线之间的夹角;L为圆弧的总长度.

计算可得K=1.14.

(2)土坡稳定安全系数的可靠度分析

对边坡稳定性分析来说,影响安全系数K的强度参数主要为内摩擦角φ与黏聚力c.对内摩擦角φ来说,现行的做法是将内摩擦系数f(tan φ)而不是内摩擦角φ作为随机变量[4].

参与计算土坡稳定安全系数K的参数均包含不确定性,因此K也包含了一定的不确定性,对其进行可靠度分析是有必要的.采用Wolff等人提出的泰勒级数法进行分析,公式如下[4],

式中,σK为土坡稳定安全系数K的标准差;δK为土坡稳定安全系数K的变异系数;ΔKi为考虑第i项参数变异性时安全系数K的差值(i=1,2,…,n,n为存在不确定性的参数的数目),ΔKi=(K1+-K1-),K1+和K1-分别为保持其它参数取平均值不变时,使用第i个参数的平均值加上一倍和减去一倍标准差求得的安全系数;δK为安全系数的变异值;E(K)为安全系数的期望值,即常规计算所得的安全系数.计算结果如表1所示.

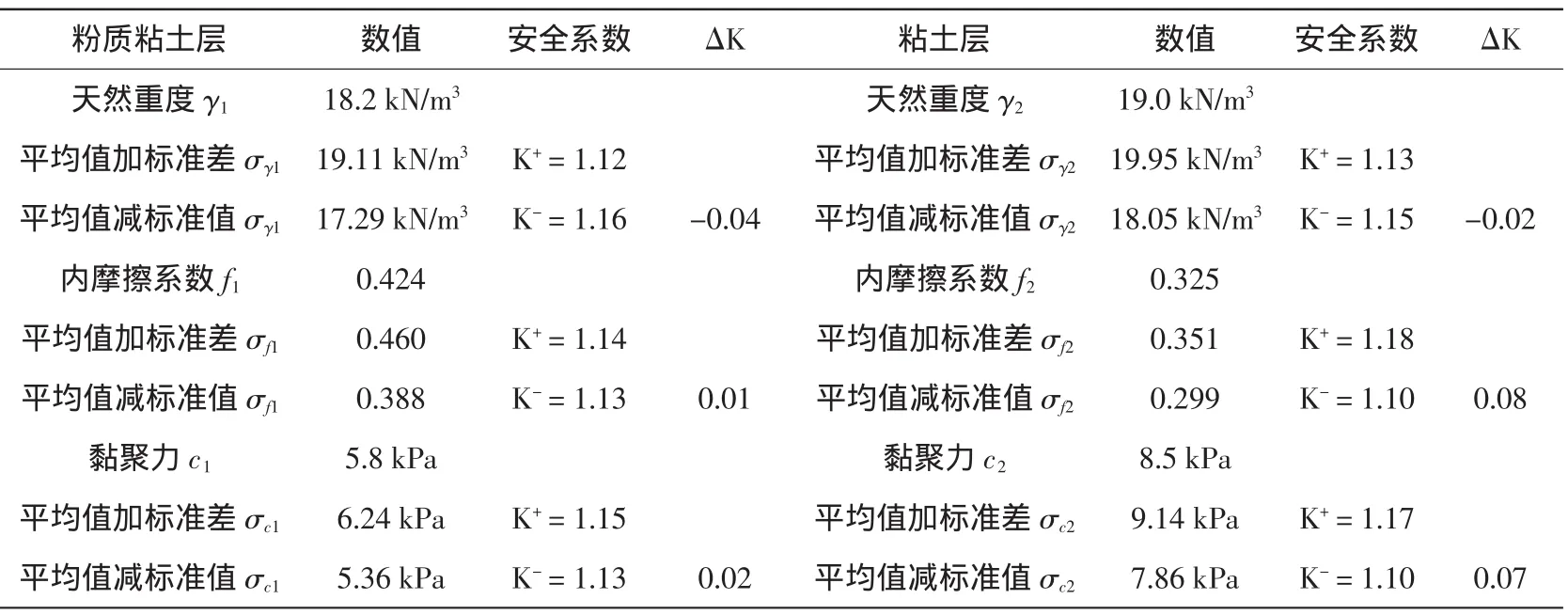
表1 泰勒级数法分析土坡稳定可靠度

由此,可以将计算参数中所包含的不确定性量化为安全系数的标准差和变异系数.将该结果代入安全系数可能服从的概率分布类型,即可求得对应的可靠度指标和失效概率.

1.3 边坡稳定失效概率

在边坡稳定性分析中,可靠度指标[5]的值是边坡状态函数(以基本变量为自变量,反映边坡完成功能状态的函数)的平均值除以状态函数标准差的商,或是在n维状态空间中,n维极限状态面至坐标原点的最短距离.在标准正态空间中,可靠度指标β与失效概率Pf有数值上的对应关系.

多数学者认为安全系数服从正态分布或对数正态分布[4-5,7-8].针对这两种不同的概率分布类型,都可以通过简单的概率计算求得安全系数的失效概率.

(1)安全系数服从正态分布

如果安全系数服从正态分布,则可通过以下公式计算出对应的可靠度指标βN,

式中,βN为正态分布下的可靠度指标;δK为安全系数的变异系数;E(K)为安全系数的期望值,即常规计算所得的安全系数.

计算可得βN=2.36,之后通过标准正态分布累积公式,即可求出安全系数对应的失效概率Pf,

式中,β为可靠度指标.

将可靠度指标βN代入式(6),可得安全系数K服从正态分布时的失效概率Pf为0.91%.

(2)安全系数服从对数正态分布

如果安全系数服从对数正态分布,则可通过以下公式计算出对应的可靠度指标βLN,

式中,βLN为对数正态分布下的可靠度指标;δK为安全系数的变异系数;E(K)为安全系数的平均值,即常规计算所得的安全系数.

计算可得βLN=2.50,将可靠度指标代入式(6)可得安全系数K服从对数正态分布时失效概率Pf为0.62%.

由此可以看出,泰勒级数法提供了一种计算可靠度和失效概率简单有效的方法,为边坡稳定性分析提供了一条新的思路.另外,上述计算中,安全系数无论是服从对数正态分布还是服从正态分布,失效概率均比较小,因此认为该边坡工程基本稳定,工作性能良好.

1.4 泰勒级数法的步骤

应用泰勒级数法对边坡稳定安全系数进行可靠度分析的步骤如下:

(1)使用各参数的平均值,采用常规理论或经验公式计算安全系数K.

(2)采用下文介绍的方法估算存在不确定性的参数的标准差.

(3)使用Excel或者其它电子表格类程序,逐一采用各参数平均值加(或减)一倍标准差后的值重新计算安全系数.计算时,每次只改变一个参数,其它参数采用平均值.这里包含2n次计算,n是存在不确定性的参数的数目.先通过计算求得n个K+和n个K-,继而求得ΔK.计算出对应不同参数的ΔK,并按照式(2)、(3)计算安全系数的标准差σK和变异系数δK.

(4)选择安全系数最可能服从的分布情况,计算其失效概率Pf.

应用泰勒级数法最主要的工作在于步骤(2)、(3)中数据分析的评估,特别是参数标准差的确定需要审慎的判断.

2 土性参数标准差的取值方法

参数所包含的不确定性将直接影响安全系数的不确定性.准确的标准差取值将使得可靠度分析的结果更加具有参考价值.根据掌握的数据资料的多少,可以通过以下方法来取得较合理的土性参数标准差.

2.1 直接计算法

如果有足够的数据,可以根据标准差的定义,直接采用以下公式计算,

式中,σ为标准差,xi为参数x第i个值,x¯为参数x的平均值,N为样本总数.

虽然这一公式的数学定义明确且便于计算,但是其实际应用往往受到样本总数的制约.当样本总数偏小时,计算求得的标准差往往也会偏小.而在实际工程中,数据往往不是很充分,而且很多参数是通过相关性估计得到的.因此在实际应用时,通过下面两种方法得到的标准差往往更加接近实际情况.

2.2 已有资料

由于我国正处在基础建设高速增长的时期,通过不同工程实践积累了大量的数据.因此在处理类似区域,类似土层的问题时,可以参考其它工程的经验.表2列举了不同地区粉质粘土物理力学参数的统计情况.在得到了相关参数的变异系数之后,即可通过以下公式计算标准差,

表2 部分地区粉质粘土物理力学参数统计表[9-14]

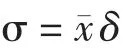
式中,σ为标准差,x¯为参数x的平均值,δ为变异系数.

2.3 三倍标准差法则(3σ法则)

三倍标准差法则是Dai和Wang[15]首先提出的,对于一个具有正态分布的参数,99.73%的数据都分布于平均值加减3倍标准差的范围之内.因此可以采用已有数据中最大值与最小值之差值的六分之一作为参数的标准差,即

式中,σ为标准差,xmax为参数x的最大值,xmin为参数x的最小值.

稳定分析中采用的岩土参数如抗剪强度指标c、φ,材料重度γ等均可以采用3σ法则在没有足够数据的情况下进行参数变异性分析.

3 工程实例

3.1 工程概况

广东佛山某房地产项目,位于佛山市南海区里水镇洲村,总占地面积约126 000 m2,塔楼超高层建筑层数为32~45层.拟建地块在道路西南侧,场地地形地貌变化大,存在高陡边坡,其周长约1 000 m,呈U形,边坡最高高度为48 m,边坡安全等级为一级.

依据地块总体规划,拟建项目随山体坡势,在场地周边分布为外环路,其路宽约6 m,对于外环路以外的边坡作为景观设计保留.在外环路以内为高层建筑群,以路面标高为小区建筑地坪,建筑群下设置为互相连通的大底盘1-4层地下室,地下室边线分布于外环路内边沿.部分区域基坑开挖作业将在现边坡坡脚下形成与开挖深度相对应高度的新人工边坡,其稳定情况将成为制约本工程成败的关键.

建设方考虑到施工过程中可能遭遇的风险,邀请本文作者为该项目提供项目咨询服务.针对该工程的特殊情况,我们表明了进行可靠度研究工作的必要性.在征得建设方同意后,对主要5个坡段采用泰勒级数法进行了可靠度分析.

现选取一代表坡段说明,如图2所示,该段坡高30 m,坡度1:1,已采用格构及坡面种植植物等支护措施,设3道马道,马道宽2 m.基坑开挖采用1:1放坡开挖,开挖深度为6 m,由于场地原因将直接在原边坡坡脚处开挖.根据地质勘察资料,该区域边坡主要由两种粉质粘土组成,土层与边坡呈逆坡向,土层倾角为10°左右,为简化计算,考虑土层为水平分布,不考虑地下水作用.

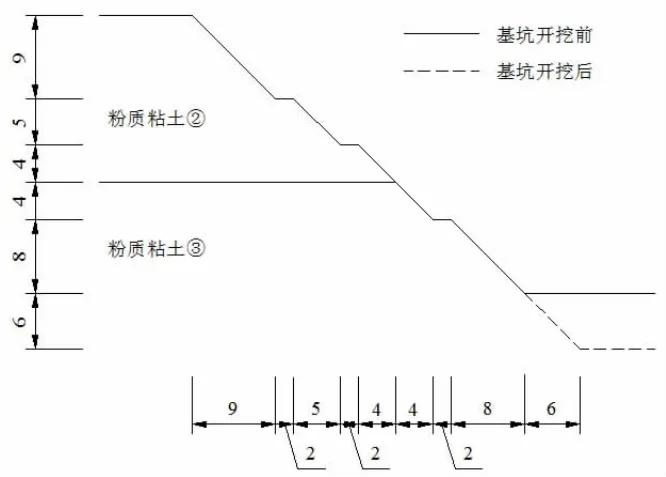
图2 基坑开挖前后边坡对比图

3.2 岩土材料参数的确定

地质勘察共取40组原位土样进行常规土工试验.分别采用上文提到的直接计算、已有资料和三倍标准差法则估算各参数的标准差,计算结果如表3所示.标准差的最终取值采用三种方法求得的最大值.

3.3 边坡可靠性分析

根据式(2)可以求得,边坡稳定安全系数为K=1.39,满足规范要求.

根据式(3),(4)求边坡稳定安全系数的标准差和安全系数,结果如表4所示.

将边坡稳定安全系数的标准差和安全系数分别代入式(5),(7)可得可靠度指标βN=1.88,βLN=2.15.

将βN和βLN分别代入式(6),可知当安全系数服从正态分布时,失效概率Pf=3.0%;当安全系数服从对数正态分布时,失效概率Pf=1.58%.为了对泰勒级数法的正确性进行验算,本文利用可靠度分析中常用的蒙特卡洛法(MC法)对本边坡进行了计算,在统计参数变量均为对数正态分布时计算的失效概率为1.48%,与本文中的计算非常接近(误差为6.33%),完全能满足工程要求.可见,虽然常规计算结果满足规范要求,但由于土性参数的不确定性,边坡还是存在一定风险的,特别当参数的变异性大于估计值时,这种失效的风险将变得更大.

表3 岩土材料参数表

表4 泰勒级数法可靠度分析

3.4 失效概率的评估和应用

失效概率的评价并没有唯一的标准,这里我们采用《地铁及地下工程建设风险管理指南》[16]中推荐的风险事故概率评定标准.

根据风险发生的概率,本工程的风险等级为四级(1%≤Pf<10%),可能发生.同时,考虑到安全系数本身满足规范要求(根据《建筑边坡工程技术规范》(GB50330-2002),边坡安全系数>1.30),参考类似工程的经验及经济性要求,我方分析认为该边坡基本稳定,无需大面积设置锚杆、挡土墙等支挡结构.但是,由于本工程边坡开挖面积较大,基坑暴露时间较长,广东地区雨季降水较多.同时考虑到场地水土保持以及文明施工等因素,必须采取对应的坡面防护及排水措施,具体建议措施如下:

(1)边坡坡顶、坡面、坡脚和水平平台应设排水系统,在坡顶外围应设截水沟;

(2)当边坡表层有积水、地下水渗出或地下水露头时,应根据实际情况设置外倾排水孔、盲沟排水、钻孔排水、以及在上游沿垂直地下水流向设置地下水廊道以拦截地下水等导排措施;

(3)开挖后的坡面应及时铺设纤维网,同时完成种草等植物防护措施;

(4)应视开挖后情况采用喷锚或格构等措施,必要时,在开挖面形成初期可先使用水泥砂浆护面;

(5)施工过程中对边坡进行严格监测,出现险情时,及时处理.

经过坡面防护后的边坡经历了广东地区雨季的强降雨天气,虽然个别区域出现了较大位移,但总体保持稳定,监测数据处于正常范围.表明泰勒级数法能较好的反映土性参数的不确定影响,对工程实际有较好的指导作用.

4 结 论

(1)尝试将泰勒级数法应用到实际工程领域进行可靠度分析.实际情况表明,泰勒级数法简单有效,可以就实际情况给出合理的可靠度分析结果.

(2)泰勒级数法使用简便,不需要比常规分析更多的数据.在原始数据不足的情况下,可以参考其他工程的经验选取相关数据计算出边坡的失效概率.

(3)泰勒级数法是以安全系数法为基础的一种可靠度分析方法,将土性参数的不确定性反应成安全系数的不确定性.在评估应用泰勒级数法的分析结果时,应结合安全系数使用.

(4)通过泰勒级数法得到的失效概率反映了安全系数小于1的概率.但是,如何将失效概率与边坡等级、工程等级、场地情况甚至施工质量挂钩仍需要在工程实践中探索.

[1]Griffiths D V,Fenton G A.Probabilistic slope stability analysis by Finite Element[J]. Journal of Geotechnical and Geoenvironmental Engineering.2004,130(5):507-518.

[2]高大钊.岩土工程的可靠性分析[J].岩土工程学报,1983,5(3):124-134.

[3]Wolff T F.Evaluating the reliability of existing levees[R].Vicksburg:U.S.Army Engineer Waterways Experiment Station Geotechnical Laboratory,1994.

[4]Duncan J M.Factors of safety and reliability in geotechnical engineering[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(4):307-316.

[5]陈祖煜.土质边坡稳定分析---原理.方法.程序[M].北京:中国水利水电出版社,2003.

[6]潘健,高珏.地基固结与沉降计算中的可靠度分析[J].汕头大学学报(自然科学版),2011,26(3):69-75.

[7]周建普,李献民,王永和.粘土边坡可靠性分析方法研究[J].湖南大学学报:自然科学版,2002,29(5):92-103.

[8]杨继红,刘汉东,秦四清,等.考虑土性参数空间变异性的边坡可靠度分析[J].工程地质学报,2007,15(2):205-211.

[9]倪万魁,韩启龙.黄土土性参数的统计分析[J].工程地质学报,2001,9(1):62-67.

[10]田小甫,孙进忠,张彬.北京地区粘性土物理力学指标统计分析[J].资源与产业,2007,9(4):80-84.

[11]张卫红.青海东部地区粘性土物理力学指标相关分析[J].青海师范大学学报:自然科学版,2009,(4):62-67.

[12]林慧常,陈伟坚.茂名地区粉质粘土的土性指标概率特征分析[J].广东土木与建筑,2007,(4):21-23.

[13]宁宝宽,杨军.沈阳粉质粘土工程指标的概率统计及分布模型[J].沈阳工业大学学报,2004,26(4):461-463.

[14]王宇辉.太原粉土工程性质指标的概率统计分析[D].太原:太原理工大学,2002.

[15]Dai S H,Wang M O.Reliability analysis in engineering applications[M].New York:Van Nostrand Reinhold,1992.

[16]中华人民共和国建设部.地铁及地下工程建设风险管理指南[M].北京:中国建设工业出版社,2007.

[17]姚耀武,陈东伟.土坡稳定可靠度分析[J].岩土工程学报,1994,16(2):80-87.