基于蒙特卡罗方法对光子束剂量沉积核的研究

苗 利 刘胜堂 孙彦泽 孔 栋 顾熹豪 李新民

（苏州大学医学部放射医学与防护学院，江苏省放射医学与防护重点实验室 苏州 215123）

放射治疗中为了能获得均匀分布的射线束野，在医用电子直线加速器中初级准直器的下方设计了均整器，使得射线束中心轴的射线质变硬，且随着离轴距离的增加，射线的能量成降低趋势。因此在射野范围内射线质是不同的，进而导致剂量的沉积也是不一样的。当光子束入射到物质中时，由于光子与物质发生康普顿散射作用，物质中某一点的吸收剂量不仅来源于该点原入射光子，而且周围散射光子对该点也具有剂量贡献。实际上，每束光子在物质中每个层面产生的剂量分布符合点扩散函数(剂量沉积核)，Varian EclipseTM[1]治疗计划系统中的AAA(Anisotropic Analytical Algorithm)剂量算法就是基于该原理，使用蒙特卡罗方法计算光子笔形束(很窄的射线束)在物质中的剂量沉积核，进而与入射光子能量注量卷积叠加得到模体内的三维剂量分布。由于笔形束剂量沉积核是离射线束中心轴距离与深度的函数，本文只研究6 MV的光子束在模体中最大剂量深度层面的剂量沉积核与不同射野下光子能谱、平均能量的影响关系。

1 材料与方法

1.1 蒙特卡罗程序

本研究使用 BEAMnrc程序[2]模拟西门子加速器(Primus) 6 MV的光子束，使用 BEAMDP子程序[3]进行相空间分析，使用 DOSXYZnrc子程序[4]进行水模体中的剂量计算，以获得剂量沉积核。经过三维水箱测量，该加速器的最大剂量深度dmax为1.5 cm。

1.2 模型建立与步骤

1.2.1 建立加速器模型

用 BEAM 程序模拟西门子加速器机头，包括靶、初级准直器、均整器、电离室、次级准直器、多叶准直器等，然后根据实测的百分深度剂量曲线和离轴比曲线对模型进行参数调整，最终使模拟曲线和测量曲线相吻合(图1)。由图1，10 cm×10 cm射野，百分深度剂量曲线最大误差 1.15%，最大剂量深度dmax层面的离轴剂量比在射野范围内最大误差 1.27%，均在误差允许范围内，加速器模型建立成功。

1.2.2 用建立的加速器模型分别模拟5 cm´5 cm、10 cm´10 cm、15 cm´15 cm、20 cm´20 cm、25cm´25 cm、30 cm´30 cm射野，并在SSD=100 cm处记录相空间(每个粒子的电量、能量、位置、方向、权重等)。

1.2.3 用 BEAMDP子程序对记录的相空间进行光子的能谱分析，得到各射野的能谱分布及射野平均能量分布，并根据能谱文件格式生成 DOSXYZnrc程序中模拟源的能谱文件，后缀名.spectrum[2,4]。

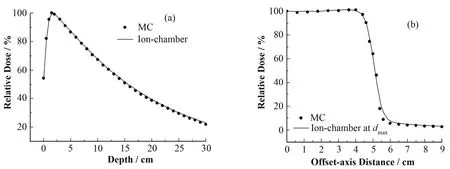
图1 蒙特卡罗计算与测量的深度剂量和离轴剂量的比较Fig.1 Comparison of MC calculated and measured depth dose profiles(a) and offset-axis dose profiles(b).

1.2.4 在 DOSXYZnrc程序中建立 30 cm´30 cm´30 cm的标准水模体，并根据需要对控制模体体素大小的X、Y、Z方向像素宽度和数目进行设置，模拟的光子笔形束的半宽为0.0005 cm[5,6]，分别用不同射野的光子能谱文件和各射野平均能量的单能光子作为DOSXYZnrc模拟源，垂直入射到模体中心，计算最大剂量深度dmax平面的剂量沉积核。理论上为了能更精准地模拟剂量沉积核，需在DOSXYZnrc程序模体描述里将记录剂量的体素尽量设小，由于采用的是笔形束，射束非常窄，随着离轴距离的增大，到达体素内粒子数迅速大量减少，造成统计误差很大。如减小统计误差就要增加模拟粒子数，但会增加计算时间。为能达到较高的计算精度和可接受的计算时间，在增加粒子数的同时设置适当的体素大小。以下计算的是X方向中心轴的剂量沉积核曲线，X与Y方向随着离轴距离的增大，采用9种体素宽度0.04、0.08、0.1、0.2、0.4、0.5、0.7、0.9、1.0 cm，Z方向最大剂量深度处设宽度为0.01 cm。运行1010粒子数，光子截断能量PCUT=0.01 MeV，电子截断能量ECUT=0.7 MeV。

1.2.5 分别比较不同射野下得到的能谱源或平均能量的单能源对剂量沉积核的影响，在同一射野下采用由该射野得到的光子能谱源和平均能量的单能光子源对剂量沉积核的影响。

2 结果

2.1 不同射野光子能量及能谱分布

用 BEAMDP程序对不同射野相空间数据进行能谱及离轴平均能量分析，结果如图2、表1所示。可见，在不同射野内光子主要集中于低能段，约为0.5 MeV，随着射野的增大，低能光子增加；而在小于1 MeV能量段内，5 cm´5 cm射野所占比例为41%，到30 cm´30 cm射野所占比例达到51%，变化高达10%。射野平均能量由5 cm´5 cm的1.70 MeV降至30 cm´30 cm射野的1.42 MeV。这是由于电子打靶后，光子束主要为前冲式辐射，侧向分散角度较小，经均整器均整后，中心轴射线束质变硬，远离中心轴的射线束质软，随着射野增大软质光子大量增加，导致平均能量降低。根据分析不同射野能谱的结果，并用相应射野的总能量注量与总注量之比得到该射野的平均能量(表1)，作为后续计算剂量沉积核时笔形束的单能源。

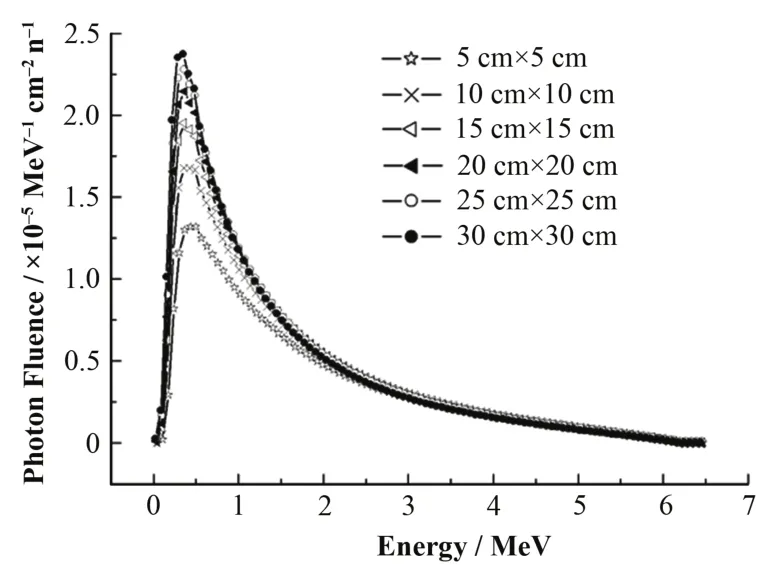
图2 不同大小射野的能谱分布Fig.2 Energy spectrum distribution of different fields.

表1 不同射野的平均能量Table 1 Mean energy of different fields.

2.2 剂量沉积核

模拟计算所得的剂量沉积核在离轴距离 2 cm范围内统计误差均小于 5%[7]。计算结果归一于5cm´5 cm射野能谱源或单能源相应中心轴沉积的剂量值(图3和图5)，纵轴均设为对数形式坐标，其中图(b)、(c)、(d)分别为(a)的局部放大，以较清楚的显示差别。

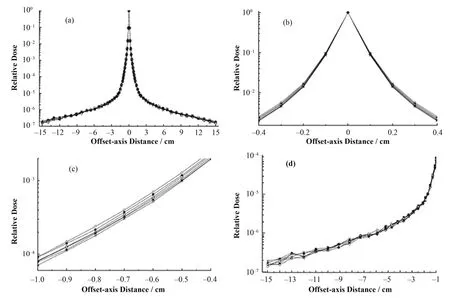
图3 不同射野能谱源产生的剂量沉积核的比较Fig.3 Comparison of dose deposition kernels of different fields using energy spectrum source. 5 cmÍ5 cm; 10 cmÍ10 cm; w 15 cmÍ15 cm; v 20 cmÍ20 cm; ê 25 cmÍ25 cm; Ð 30 cmÍ30 cm

2.2.1 不同射野能谱源的剂量沉积核比较

图3为使用不同射野下能谱作为模拟源计算得到dmax层面的剂量沉积核。中心轴点的剂量随获得能谱源的射野而增大，且增大幅度逐渐减小(图4)。在离轴1 cm范围内，同一离轴距离处剂量沉积随获得能谱源射野增大而减小，在图(b)、(c)中，能较为清楚地看到利用小射野获得的能谱源的剂量核要比大射野时的宽，即同一离轴距离处剂量值要高。在离轴距离大于1 cm时，六个剂量核出现了不同程度的波动，这是由远离中心轴剂量沉积量小和统计误差引起的。对于六个剂量核，用同一离轴距离处百分剂量沉积值减5 cmÍ5 cm射野能谱源的百分剂量沉积值，所得最大、最小的百分剂量差分别为1.47%和−1.21%，其中最大值出现在中心轴点，最小值出现在离轴0.1 cm附近。

2.2.2 不同射野平均能量单能源的剂量沉积核比较

图5为利用不同射野下平均能量的单能源作为模拟源计算得到dmax层面的剂量沉积核。中心轴点的剂量沉积随单能源能量的减小而增加，且基本以线性方式增长(图6)。在离轴0.7 cm范围内，在同一离轴距离处，高能源比低能源的剂量沉积多。由图5(b)、(c)，能较为清楚地看到使用高能源获得的剂量核要比低能源的宽，即同一离轴距离处剂量值要高。当离轴距离大于0.7 cm时，六个剂量核出现了不同程度的波动，也是由于远离中心轴剂量沉积量小和统计误差引起的。对于这六个剂量沉积核，用同一离轴距离处百分剂量沉积值减5 cmÍ5 cm射野单能源的百分剂量沉积值，所得最大、最小的百分剂量差分别为6.28%和−0.33%，其中最大值出现在射束中心轴点，最小值出现在离轴0.1 cm附近。

图4 不同射野能谱源产生的中心轴相对剂量Fig.4 Relative dose of center-axis for energy spectrum source of different fields.

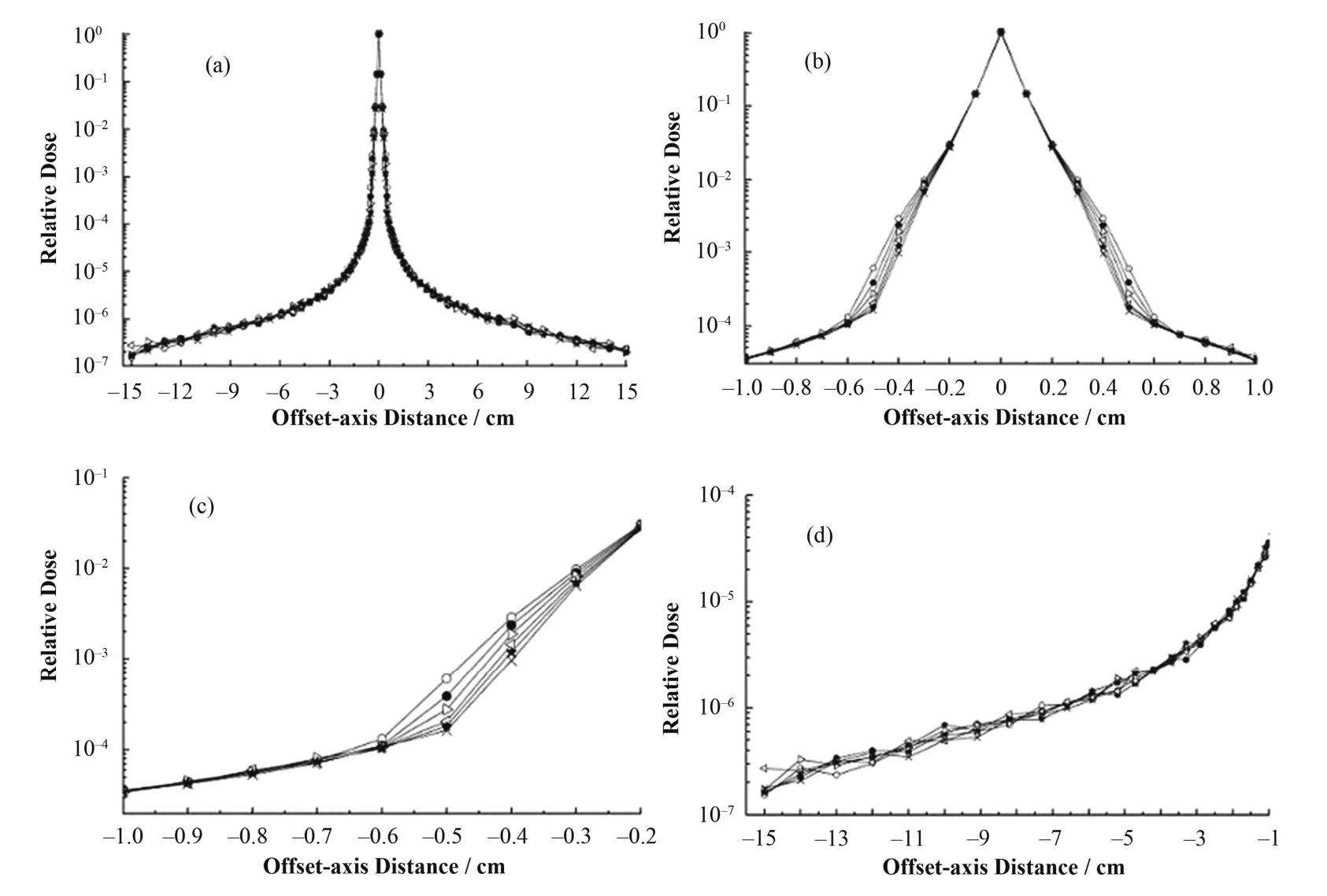
图5 不同射野的单能源产生的剂量沉积核的比较Fig.5 Comparison of dose deposition kernels of different fields using mean energy mono-energy source. 5 cmÍ5 cm; 10 cmÍ10 cm; w 15 cmÍ15 cm; v 20 cmÍ20 cm; ê 25 cmÍ25 cm; Ð 30 cmÍ30 cm

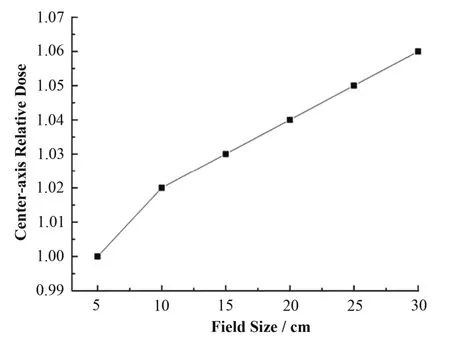
图6 不同射野单能源产生的中心轴相对剂量Fig.6 Relative dose of center-axis for mono-energy source ofdifferent fields.

2.2.3 同一射野下采用能谱源与平均能量单能源作为模拟源的剂量沉积核比较

分别将模拟的各射野下获得的能谱源与单能源剂量核进行比较，剂量归一点为每对数据由能谱源得到的中心轴剂量。在六组数据的比较中，同一离轴距离处用能谱源与单能源百分剂量沉积值相减，得到最大百分剂量差都在 9%以上，甚至达到13.2%，最小差值为−4.14%，其中最大值出现在射束中心轴点，最小值出现在离轴0.1 cm附近。同时，随着射野的增大，从相应射野得到的两种模拟源剂量沉积核的百分剂量差都在逐渐变大，且最大百分剂量差的变化幅度大于最小百分剂量差的变化(图7)。

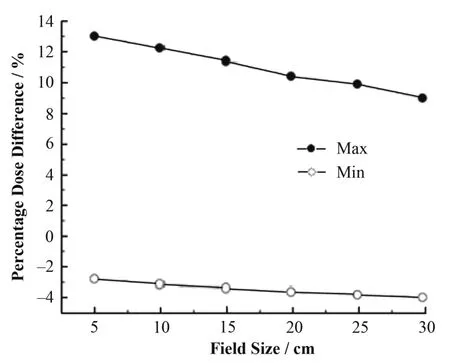
图7 同一射野下采用不同源产生的剂量核的百分剂量差Fig.7 Percentage dose difference of dose kernels using different simulant sources from same field.

3 结语

均整器的设计使得射野增大时低能光子增加，能谱构成发生变化，虽然从5 cm´5 cm到30 cm´30 cm 射野能谱中低能光子(小于 1 MeV)变化高达10%，但是利用相应能谱模拟源在最大剂量深度层面得到的剂量沉积差别并不大，中心轴处百分剂量差值最大相差1.47%，在可接受范围内。而由5cm´5 cm射野得到的平均能量 1.70 MeV 降至30cm´30cm射野时的1.42 MeV，而在水中最大剂量沉积变化高达 6.28%。在由同一射野下得到的能谱源与单能源的剂量沉积核的比较中，最大的剂量差高达13.2%。

综上所述，光子的剂量沉积核具有能谱与能量依赖性，但对于能谱源来说依赖性较小，原因在于dmax之前的建成层吸收低能的光子，由射野大小不同引起能谱的变化对更深层面剂量的影响并不大。由于整个射野内能量分布并不是单一的，如果只用某一单能源，对剂量计算将会造成很大误差，比较精确的计算剂量的方法是使用能谱源。

上述研究由于只针对单一笔形束，最大、最小剂量差出现在离轴0.1 cm范围内，随着离轴距离的增加误差也迅速变小，在离轴0.2、0.4、1 cm处剂量百分剂量差数量级分别在 10−1、10−2、10−3，对于整个射野剂量来说将是无数个笔形束的效应之和，射野内的任何一个点的剂量都来自周围无数点的散射贡献，如果单一笔形束的剂量计算误差较大，那么在通过卷积叠加效应后，误差会更大。

1 Tillikainen L, Helminen H, Torsti T, et al. A 3D pencil-beam-based superposition algorithm for photon dose calculation in heterogeneous media[J]. Phys Med Biol, 2008, 53(14): 3821–3839

2 Rogers D W O, Walters B, Kawrakow I. BEAMnrc Users Manual[R]. NRCC Report PIRS-0509(A) revL, 2011

3 Ma C M, Rogers D W O. BEAMDP as a General-Purpose Utility[R]. NRCC Report PIRS-0509(C) revA, 2009

4 Walters B, Kawrakow I, Rogers D W O. DOSXYZnrc Users Manual[R]. NRCC Report PIRS-794 revB, 2011

5 Kirkby C, Sloboda R. Comprehensive Monte Carlo calculation of the point spread function for a commercial a-Si EPID[J]. Med Phys, 2005, 32(4): 1115−1127

6 Steciw S, Warkentin B, Rathee S, et al.Three-dimensional IMRT verification with a flat-panel EPID[J]. Med Phys, 2005, 32(2): 600−612

7 Warkentin B, Steciw S, Rathee S, et al. Dosimetric IMRT verification with a flat-panel EPID[J]. Med Phys, 2003,30(12): 3143−3155