正八面体含氢晶格中子内源全息成像的初步模拟研究

曹 超 孙 勇 唐 彬 霍合勇

（中国工程物理研究院 核物理与化学研究所 绵阳 621900）

全息成像的概念最早由D. Gabor在1948年提出，目的是提高电子显微镜的分辨能力至原子尺度。由于源和探测器的实现比较困难，微观全息成像技术的发展陷于停滞，直到1986年Szöke[1]提出可用内源全息法探测固体内部原子排列信息，电子、硬X射线和γ射线等才开始陆续被作为原子分辨率全息成像的探针，并成功实现了Cu、SrTiO3等晶格结构的三维重构，但均受制于样品穿透力和原子核外电子的干扰，虽然中子在这方面有较大优势，但受制于束流强度，难以得到实际应用。

2001年，Cser等[2]提出中子全息成像的概念。同年，Sur等[3]在加拿大NRU反应堆上首次进行了验证性实验，用中子内源全息法对 Al4Ta3O13(OH)的晶体结构进行重建。之后，Cser等[4−7]在法国ILL研究堆、ORR研究堆以及在日本JRR-3反应堆上分别检测了Pd-H0.78、Pb-Cd0.0026等晶体的晶格结构，获得与衍射实验等相符的结果，特别是成功分辨出了在混入Cd杂质后Pb金属晶体中原子间距的微小变化，精度高达10−3−10−4nm量级。2010年，在匈牙利Budapest研究堆上建成了专门用于中子全息成像的实验装置[8]，并对结构较为复杂的 Sn-Cd0.0026和NH4Cl晶体进行了测定，获得了令人满意的结果。另一方面，全息成像的重建算法也在不断改进，如Markó等[9]提出的 DR双重重建算法，通过同时记录分析内源散射中子和内探测器散射中子进一步提高重建精度；Sur等[10]提出的K线反解方法，将中子全息术推广到多源核系统；Gähler等[11]将极化中子的自旋变化作为宏观参考波，从而可以分辨样品内部磁结构分布。

由此可见，中子全息成像技术获得了飞速发展，其将中子成像的能力拓展至原子层面，为基础科学、材料学、医学、生物学等研究提供了有力的观察手段。但无论在算法或硬件方面，中子全息成像技术还存在很大的发展和完善空间，特别是在国内该技术还处于空白，缺乏相关的理论和实验基础，仅凭国外文献难以对成像原理、实验技术等有深入了解。本文采用数值方法模拟正八面体含氢晶格的中子内源法全息成像和重建过程，并分析统计噪声、探测波长等关键参数对成像结果造成的影响，为进一步开展理论和实验工作奠定基础。

1 原理

中子全息成像的基本思想是基于光学全息原理，利用中子激发样品内不同位置的原子，使其分别产生物波和参考波，并相互叠加生成可被记录的宏观二维全息图像，通过反解全息图最终得到原子的三维排布[2]。

图1所示为内源全息术示意图。考虑单原子情况，外中子束经源核散射后以球面波的形式传播，其中一部分直接到达距离源核Rr处的探测器(参考波)，另一部分被邻近原子核散射后再到达探测器(物波)。设探测波动量为k，则参考波波幅为

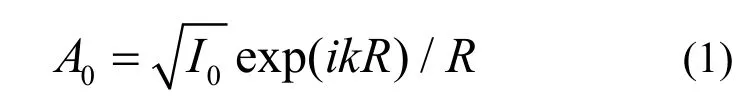
式中，I0为外中子束经源核散射后的源强。另一方面，内源波经距离源核jrr的原子散射一次后形成的物波波幅为

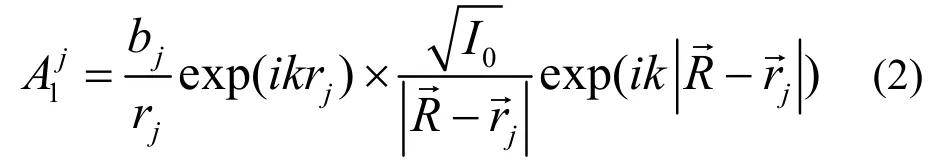
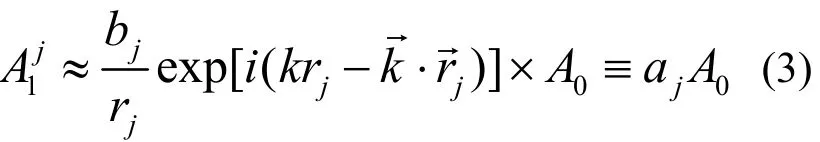
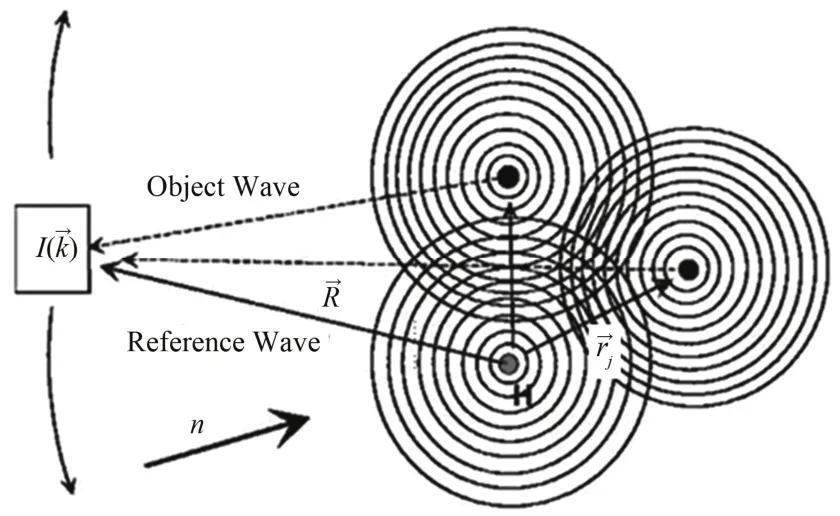
图1 内源全息术示意图[12]Fig.1 Principle of inside-source holography[12].

与探测器与散射核的坐标矢量相关。将中子计数器作为探测器，通过转动探测器(或样品)获取不同方向上的中子强度，形成二维全息图

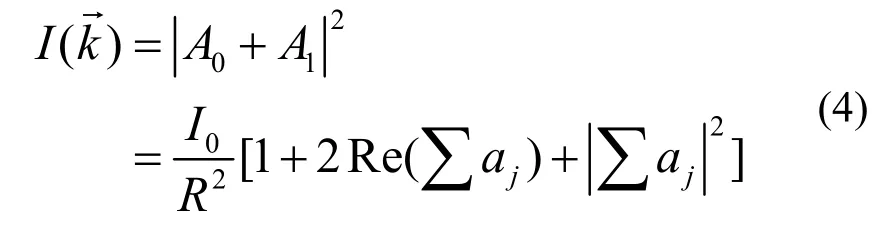
式中第一项参考波幅为恒定值，可作为背景项，第三项物波幅为二阶小量，可忽略，因此全息图主要由第二项全息干涉项决定。

利用Helmholtz-Kirchhoff变换对全息图进行重建

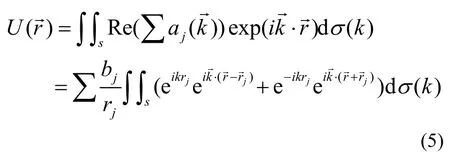
由于待检样品实际上包含多个原子，因此实验中需要作如下限定：

(1) 样品具有大量重复的原子排列结构，即要求晶体对象；

(2) 晶体尺寸远小于探测器距离，使各单元全息图近似在同一位置产生，一般晶体尺寸在mm量级，则探测器距离需在10 cm以上；

(3) 各单元全息图可直接叠加，即要求非相干源波，由于氢核具有较大的非相干散射截面(79.91b)和较小的相干散射截面(1.8b)，因此含氢晶体是内源法主要的检测对象。

2 模拟及关键参数分析

2.1 实验布局及关键参数

中子全息成像实验一般采用如下布局：外中子束、样品和探测器处于同一平面，通过转动样品同时改变样品与探测器的相对位置，由于只需旋转样品，避免了探测器在大范围内的移动，大幅减小了操作空间。

有很多因素会影响成像结果，包括探测器的统计噪声、探测波长、取样角分布、仪器分辨率、散射中子等，其中统计噪声是固有影响；探测中子波长、探测器尺寸，仪器分辨率等参数是装置研制和建设中首要解决的问题；探测器计数、取样角分布等是实验测量中需要确定的参数。本文采用数值计算工具对内源全息法的干涉成像和重建过程进行模拟，并分析其中部分关键参数，以得到初步结论。模拟晶格如图2所示，为正八面体，仅考虑最近邻原子的排列结构，中心为源核，各顶角为散射核，坐标系 保持样品不动，以源核为坐标原点，各散射核分别位于 x、y、z轴上，kr矢量取为(ksinθcosφ,ksinθsinφ, kcosφ)。以下分析所称原子间距r均为源核与散射核距离，如无特殊说明，r取0.2 nm，探测波长取0.1 nm，θ、φ取样间隔2°。

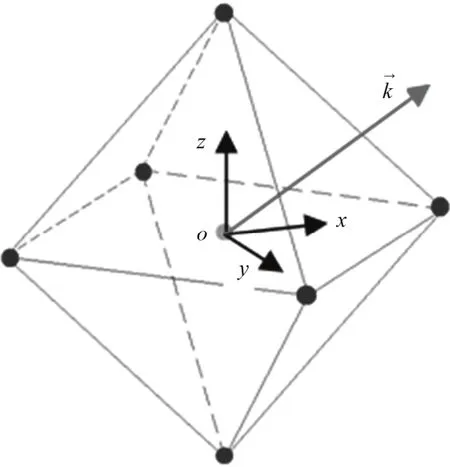
图2 正八面体晶格Fig.2 Ortho-octahedron lattice.

2.2 理想情况

理想情况下(不考虑实验误r差r)， 二维全息图可直接由 a =(b/r) exp[i(k r - k ×r )]得到(图3)。

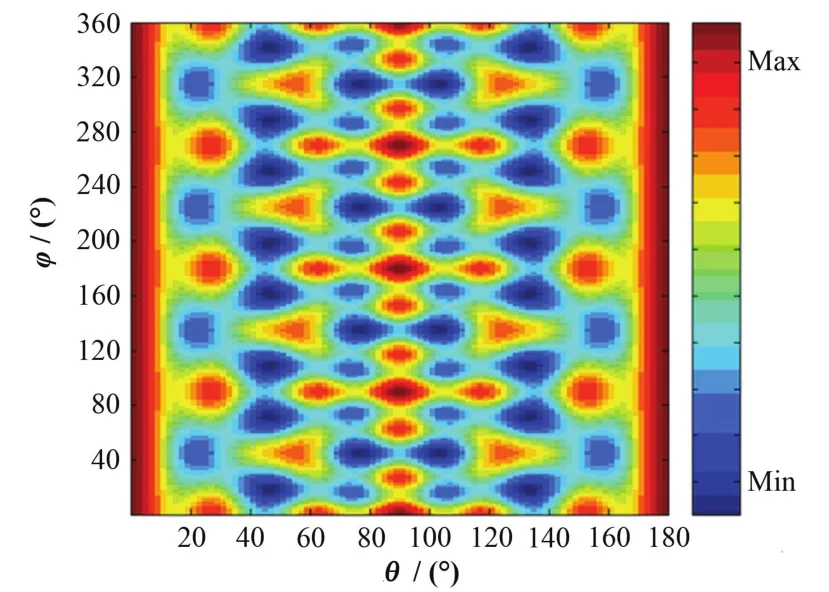
图3 理想情况全息图Fig.3 Ideal hologram.

重建则基于式(5)，其可改写为

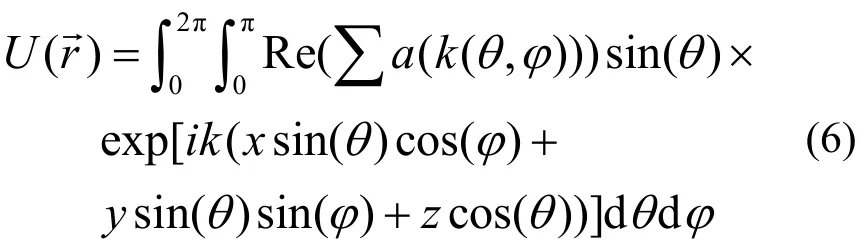
为减少计算量，只选取z=0平面做计算，并将连续积分转换为离散求和，图4为重建结果。

2.3 统计噪声(探测计数)

探测器的中子计数遵从泊松分布，各探测点的平均噪声近似为该点探测计数的平方根。而由式(4)，各散射原子的有效信号仅为背景的 10−5−10−3倍(取决于散射长度b与原子间距的比值r)，只有当各点计数值达到106−1010量级以上时，全息图的有效信号才大于统计噪声。

实际上这一计数限制可以大幅放宽，即使各点的信噪比较低，也可能获得较好的重建结果，Markó等[13]曾对此进行过一些解析分析，其原因主要在于积分重建，式(5)实质上是对全息图上每个点的探测数据按一定相位进行叠加，假定总的探测点数为N，各点的背景计数为I，则各点有效信号约为因此重建结果的信噪比量级可较全息图中的单点信噪比高出约N1/2倍。

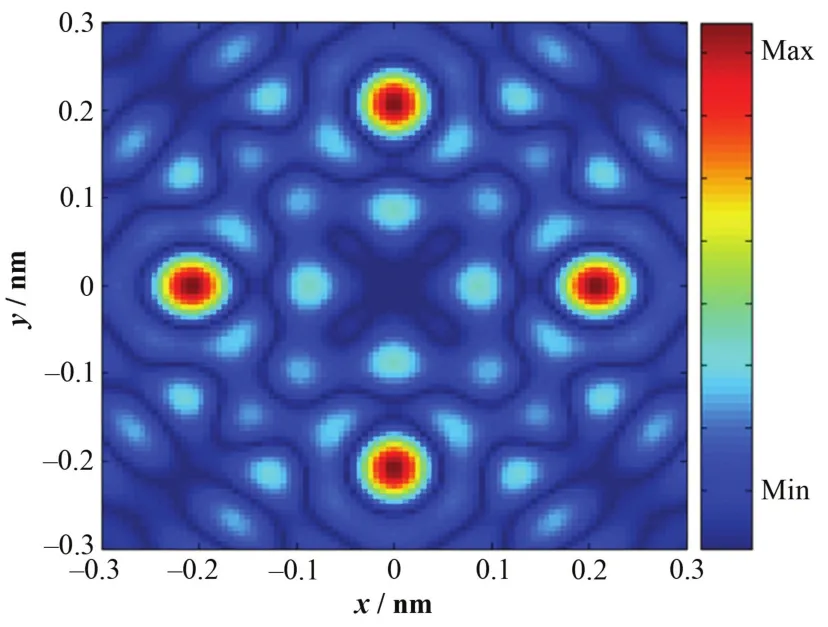
图4 理想全息图重建Fig.4 Holographic reconstruction from ideal hologram.

可见噪声对重建结果的影响主要取决于三个参数：b/r值、单点背景计数I以及总探测点数N。其中b/r和I决定了二维全息图的单点最大信噪比：值则决定了重建后的信噪比增益。对噪声影响进行数值模拟，为充分保证采样质量，取样角间隔设为2°，即N值取为16200，I取为5×105，通过设定不同的b/r值改变单点信噪比(也可以固定b/r并改变I值，结果近似)，为进一步减弱泊松噪声对背景计数的波动影响，将各点计数求和平均后作为背景并减去得到全息计数。图5列出了最大信噪比为1、1/10和1/30时的全息图及其重建：当单点信噪比为1时，全息图与重建图均与理想情况类似(重建图中心的亮点源于噪声引发的背景消除不完全)；信噪比为 1/10时，虽然全息图上的信息大部分被噪声湮没，但重建结果并未受到大的影响；而当单点信噪比低至1/30时，重建结果出现较大失真，但仍能粗略得到原子坐标信息，此时重建信噪比约在2。

由于全息成像的特殊重建性质，可以在实验时适当降低探测计数以提高效率，但应注意实际操作中还存在其他误差因素，而泊松噪声会放大这些因素的干扰，因此选择时需综合考虑实验因素和探测效率。

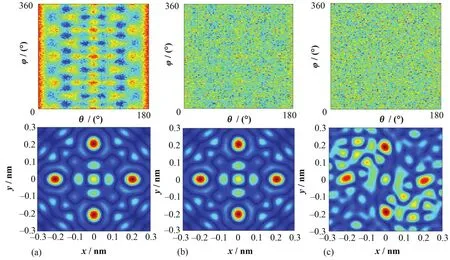
图5 不同信噪比下的全息图及其重建Fig.5 Holographic reconstruction with different SNR.(a) 1; (b) 1/10; (c) 1/30

2.4 探测中子波长

探测中子波长是关键参数，其选择关系到仪器排布、成像效率和成像质量。由于全息成像实质上是利用中子与原子核作用后波动的相位变化进行观测，因此探测波长越短，相位变化越明显，坐标的分辨精度也越高。图6列出了中子波长在0.05、0.15、0.25和0.3 nm情况下的全息重建图(0.1 nm情况见图4)。由图6，短波长中子的分辨精度明显更高，当波长大于原子间距时，重建结果出现明显失真。

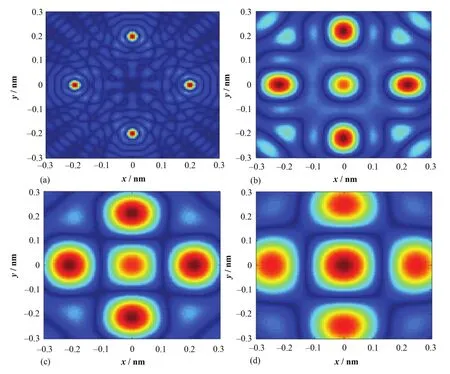
图6 不同探测中子波长的全息重建图Fig.6 Holographic reconstruction with different neutron wavelength.(a) 0.05 nm; (b) 0.15 nm; (c) 0.25 nm; (d) 0.3 nm

图7列出原子间距分别为0.2和0.5 nm时不同波长深测中子的一维重建图，二维积分重建引入的振荡项在图中表现为各种波形，包括峰值明显较高的主波和一系列次级波。由图 7，主波的波峰并未落在真实原子坐标上，且偏移量与原子间距、波长等不存在明显关系。此处对其产生机理进行分析，考虑一个较简单的情况：存在两个关于原点对称的原子，坐标分别为(c,0,0)和(−c,0,0)，其在式(5)中实际上贡献了四个积分

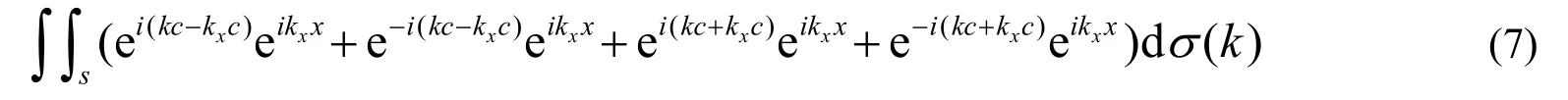
式中，一、三项为相互对称的原像，二、四项为其共轭像，峰值坐标应分别为(c,0,0)、(−c,0,0)、(−c,0,0)、(c,0,0)，以波长0.1 nm、c=2、取样角间隔4°情况为例，图8分别列出个四个像的一维重建图(此时式(7)的实部远大于虚部，因此用实部代替绝对值)。由图8，原像的主波峰值坐标与实际坐标完全一致，重建坐标的偏移实际上由原像的主波和其对称像、共轭像的次级波混叠造成，即第一与二、三项发生混叠、第三与一、四项发生混叠，由于这些次级波的分布同很多因素有关，包括中子波长、步进角、原子间距等，并无明显规律，因此叠加后会对主波峰造成微小偏移。

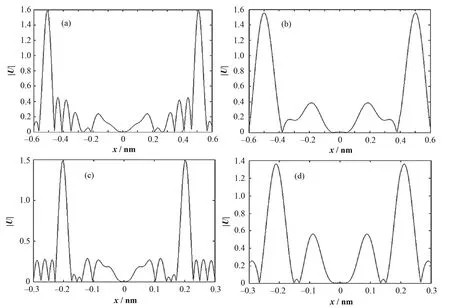
图7 不同探测波长和原子间距下的的一维理想重建图Fig.7 Ideal 1-dimensional holographic reconstruction with different neutron wavelength and neighbor atom distance.(a) 0.5 nm distance, 0.1 nm wavelength; (b) 0.5 nm distance, 0.2 nm wavelength;(c) 0.2 nm distance, 0.05 nm wavelength; (d) 0.2 nm distance, 0.1 nm wavelength

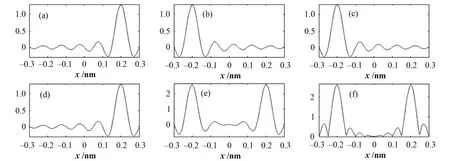
图8 原像及共轭像的一维重建图(a) (2,0,0)原像；(b) (2,0,0)共轭像；(c) (−2,0,0)原像；(d) (−2,0,0)共轭像；(e) 前四幅图叠加；(f) 叠加后取模Fig.8 Ideal 1-dimensional holographic reconstruction of original and conjugate images.(a) (2,0,0) original; (b) (−2,0,0) conjugate; (c) (−2,0,0) original; (d) (−2,0,0) conjugate;(e) superposition of (a)−(d); (f) absolute value of (e)

事实上，全息成像中每个原子都会受到其共轭像和其余原子的影响，特别是在中子全息等微观射线全息术中，原像与共轭像沿同一方向传播并同时被记录(同轴全息)，即使只有一个原子，其共轭像也可能造成原像的偏移。Markó 等[14]也观察到类似现象并进行了解释，重建坐标的偏移源于二维积分重建，通过分别记录多个波长中子的全息图并进行叠加可能将次级振荡的影响减小甚至消去。由图7，随着探测中子能量的提升，振荡效应逐步明显，主波与次级波的混叠区域变窄，最大偏移量也会逐渐变小。

尽管理论上探测中子的波长越短越好，但应该注意：(1)能量越高的中子与物质反应截面越小，单色化越困难，全息粒子数及探测器效率也会相应地降低；(2)反应堆的中子能谱存在限制，高能段的中子注量率迅速衰减，通常只能在峰值附近进行选取；(3)重建坐标偏移随探测中子波长呈无规则变化，当中子能量相差不大时，短波长的优势并不明显。由于晶格原子间距一般在0.1 nm以上，反应堆热中子注量率峰值也出现在0.1 nm左右，因此探测中子波长在0.1 nm左右进行选取较为合适。

2.5 取样角分布

取样角分布即样品转动的步进角，其最大采样间隔可由Nyquist定理确定，以x轴正方向上的原子核(r,0,0)为例，有全息项

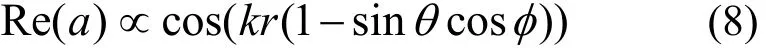
对式(8)作频谱分析，由于二维球面坐标上难以直接定义傅立叶变换，可通过固定一方位角对另一角作一维傅立叶分析，分别确定其频域。而根据被固定角取值的不同，另一方位角的频域也会发生变化，此处取最大频域，分别对应于θ固定为90°和f固定为180°情形，频谱分析结果如图9所示。由图9，两方位角均有截止频率fmax≈2.65，其对应的最大抽样间隔为 δmax=1/(2fmax)≈0.19，即 10.8°。

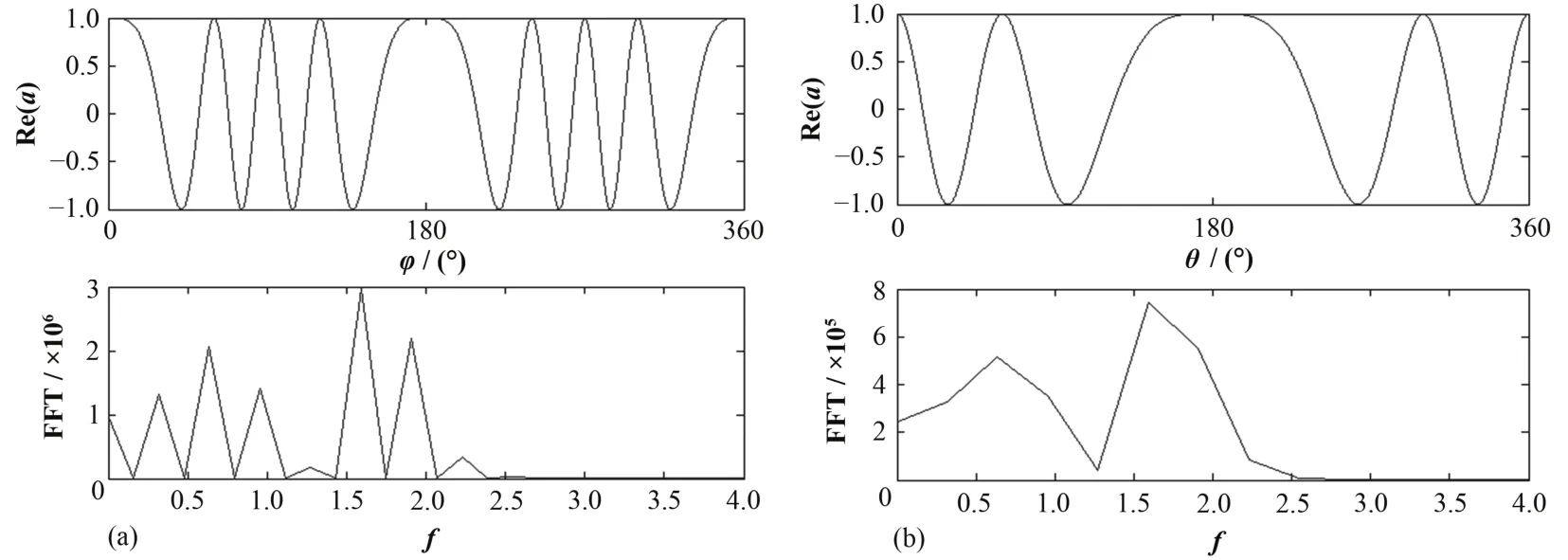
图9 全息项的频谱分析(函数及频谱)Fig.9 Frequency analysis of holographic term (function and spectrum).(a) Re(a(θ=90°,φ)); (b) Re(a(θ,φ=180°))

图10 列出了步进角分别在10°、12°和15°的重建结果，与图4比较可以发现，步进角10°的重建结果与2°基本一致；步进角增至 12°时，抽样函数频谱发生混叠，表现为重建图四周出现强度不高的“赝像”，此时重建结果仍可接受；当步进角增至15°时，混叠效应明显加强，不仅重建峰发生形变，同时赝像强度与实像接近，难以分辨。

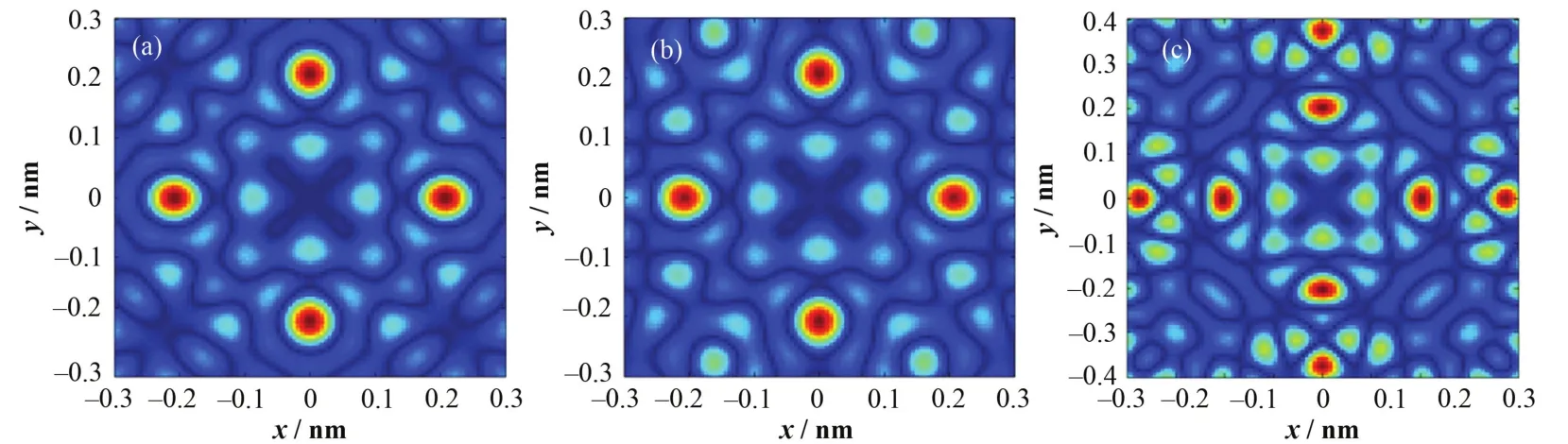
图10 不同步进角的全息重建图Fig.10 Holographic reconstruction with different angular step width.(a) 10°; (b) 12°; (c) 15°

上述进行的步进角分析仅限于原子间距为 0.2 nm的最近邻原子，而由式(8)，全息项Re(a)的频谱与其余弦函数中的系数rk密切相关，rk值越大，截止频率fmax越高，相应的取样间隔也越小。因此考虑到外层原子贡献，实际步进角还应小于10.8°。目前实验常用的步进角为1°−5°。

2.6 探测器张角

重建与分析均基于理想的点探测器模拟，但在实际操作中，探测器的体积往往不能忽略，会占据一定的方位角。Markó等[14]曾对其影响进行分析，假定探测器的中子计数与探测张角关系满足高斯分布，则随着探测张角的增大，离源核较远原子的重建峰振幅会受到一定的抑制。

但在一种更极端的情况下，即假定面探测器可完全探测到其张角内的中子，取原子间距为0.5 nm，取样点间隔5°，不考虑统计噪声，将点探测器与张角为5°×5°面探测器的重建结果进行对比(图11)，结果显示，探测器张角对重建精度影响不大，重建峰的展宽和偏移变化几可忽略，但峰值的确出现了抑制，对信噪比造成一定影响。另外探测器张角越大，接收到的干扰中子也越多，因此仍需要根据实验环境进行选择。

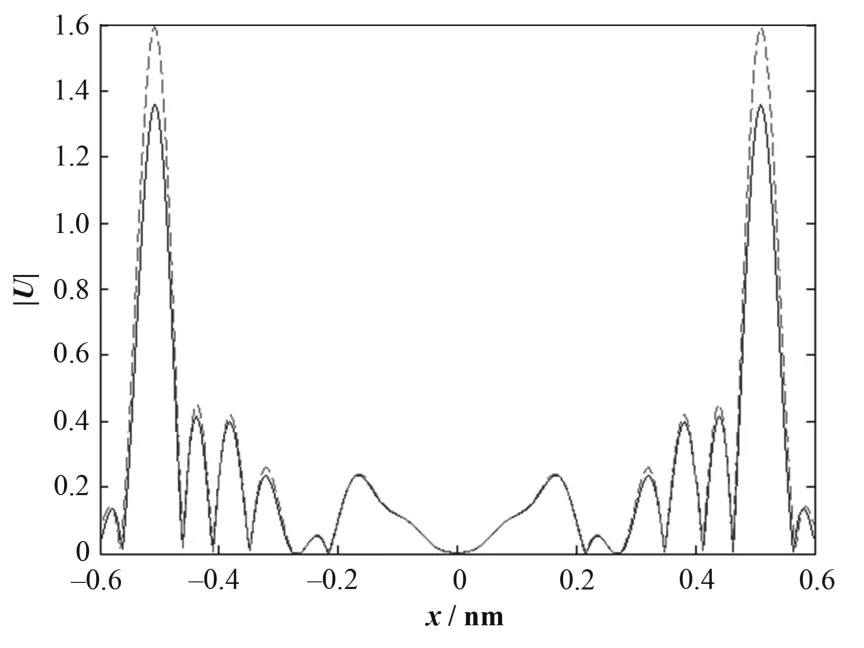
图11 点探测器和面探测器的一维全息重建图---- 为点探测器；— 为面探测器Fig.11 1-dimensional holographic reconstruction with different detector.---- point detector； — surface detector

3 结语

本文简单介绍了中子全息成像技术的原理和发展，并根据成像原理对正八面体含氢立方晶格的内源全息成像进行了数值模拟和重建，并对部分关键实验参数进行了分析：

(1) 分析泊松噪声对重建结果的影响，并通过数值模拟验证了重建结果信噪比与二维全息图信噪比之间的增益关系。

(2) 分析探测中子波长对重建质量的影响，波长应小于原子间距，且波长越短，分辨精度越高；发现重建坐标与原坐标之间产生的偏移现象并分析其原因，源于二维积分重建三维坐标引发的振荡项；根据探测效率要求和模拟结果分析探测中子波长的选择范围。

(3) 给出样品转动步进角的选取方法并进行验证。

(4) 通过数值模拟验证了探测器张角对重建峰峰值的抑制。

结果表明数值模拟技术是中子全息成像技术研究的有效辅助手段，在后续工作中，我们将基于此方法对重建算法和其他参数展开研究，为理论和实验工作奠定基础。

1 Szöke A. X-ray and electron holography using a local reference beam[C]. In Short Wavelength Coherent Radiation: Generation and Applications, edited by T.Atwood and J. Boker, AIP Conf. Proc. 147 (AIP, New York), 1986. 361−367

2 Cser L, Krexner G, Török Gy. Atomic-resolution neutron holography[J]. Europhys Lett, 2001, 54: 747−752

3 Sur B, Rogge R B, Hammond R P, et al. Atomic structure holography using thermal neutrons[J]. Nature, 2001, 414:525−527

4 Cser L, Török Gy, Krexner G, et al. Holographic imaging of atoms using thermal neutrons[J]. Phys Rev Lett, 2002,89: 175504

5 Cser L, Török Gy, Krexner G, et al. Neutron holographic study of palladium hydride[J]. Appl Phys Lett, 2004, 85:1149

6 Cser L, Krexner G, Markó M, et al. Direct observation of local distortion of a crystal lattice with picometer accuracy using atomic resolution neutron holography[J].Phys Rev Lett, 2006, 97: 255501

7 Hayashi K, Ohoyama K, Orimo S, et al. Neutron holography measurement using multi array detector[J].Japan J Appl Phys, 2008, 47: 2291−3

8 Markó M, Szakál A, Török Gy, et al. Construction and testing of the instrument for neutron holographic study at the Budapest Research Reactor[J]. Rev Sci Instru, 2010,81: 105110

9 Markó M, Krexner G, Schefer J, et al. Atomic resolution holography using advanced reconstruction techniques for two-dimensional detectors[J]. New J Phys, 2010, 12:063036

10 Sur B, Anghel V N P, Rogge R B, et al. Diffraction pattern from thermal neutron incoherent elastic scattering and the holographic reconstruction of the coherent scattering length distribution[J]. Phys Rev B, 2005, 71:014105

11 Gähler R, Ignatovich V. Neutron holography without reference beams[J]. Phys Lett A, 2007, 362: 393−400

12 Cser L, Török Gy, Faragó B, et al. Experimental observation of neutron holography on atomic level.[EB/OL]. http://fizika.fazekas.hu/fazekasban/Torok.pdf.

13 Markó M, Cser L, Krexner G, et al. Theoretical consideration of the optimal performance of atomic resolution holography[J]. Meas Sci Technol, 2009, 20:015502

14 Markó M, Cser L, Kexner G, et al. Instrumental distortion effects in atomic resolution neutron holography[J]. Phys B,2006, 385−386: 1200−1202