某地浸铀矿床低渗透性砂岩孔隙结构特征研究

曾 晟 谭凯旋 雷 林 李春光 王富林

（南华大学 核资源工程学院 衡阳 421001）

大量研究表明，砂岩孔隙结构包括孔隙大小和分布、孔隙和喉道的连通关系、孔隙的几何形态和微观非均质特征、孔隙中粘土矿物成分及产状等，其孔隙微观结构具有较强的分形特征[1–4]。近年来，研究人员大部分是利用分形理论来研究油储层、土壤、煤矿等多孔介质的结构特征[5,6]。多孔介质孔隙结构的物理特性可以用多种多样的指标来描述，例如孔径、孔喉、孔表面积、孔的体积、孔隙度、孔隙结构的分维值等。其中最重要的为孔隙度，即孔隙的体积与样品总体积的比值。可地浸低渗透性砂岩型铀矿岩孔隙微观结构也是一种典型的多孔介质。原地浸出采铀是将溶浸液直接注入含矿岩层中，利用有用矿物与水溶液的化学反应来获取有用金属和化合物的一种集采矿、选矿、冶金于一体的环境友好的采矿方法。在原地浸出采铀过程中，含矿层砂岩孔隙结构将直接影响有用成分的浸出率[7,8]。由于含矿层砂岩微观孔隙结构特征控制和影响浸出液在孔隙性岩石中的流动分布、渗滤特征和反应机理。开展可地浸开采砂岩孔隙结构研究，掌握低渗透性含铀砂岩孔隙结构特征这一直接影响铀矿地浸开采的客观因素，对地浸采铀高效开采有重要意义[9,10]。在地浸采铀过程中，溶浸液在含矿岩层孔隙中的流动-反应-物质运移等都与孔隙的连通性、孔隙的大小、孔径的走向等有密切关系，铀的高速浸出都决定着溶浸剂渗透含矿层的程度。因此研究铀矿岩内部微观孔隙的结构特征有重要的理论现实意义。

目前压汞法研究多孔介质孔隙结构的分形特征已取得了一些成果，已经建成了毛细管模型和球形模型等计算多孔介质的孔隙分维值的数学模型。利用压汞实验获得的各种参数来研究孔隙介质的分形特征，主要有：利用毛细管模型结合汞的饱和度与注入汞的压力之间的关系研究了多孔介质孔隙的分形结构；利用毛细管模型结合累积孔隙体积与注入汞的压力之间的关系研究了石油储层的孔隙结构分形特征；利用毛细管模型和压汞实验数据中的孔径和侵入体积(入口半径-孔隙体积模型)研究了孔隙的分形特征等[11−14]。本文在对多孔介质孔隙结构分形特征研究的基础上，基于压汞毛管压力曲线，研究了某地浸采铀矿山低渗透性含矿层的孔隙结构特征，为渗透性砂岩铀矿原地浸出采铀理论技术研究提供理论基础。

1 理论基础

1.1 压汞法原理

压汞法首先是由里特和德列克于 1945年提出的[15]。它基于水银对固体表面的不可润湿性，要在外部压力作用下才能挤入固体小孔，因此外部压力就可作为孔大小的量度。人们普遍接受多孔固体材料中的气孔为圆柱形这个具有实际意义的模型，由于液态汞与固体材料的接触角大于 90°，且表面张力很大，对多数材料具有不润湿性，因此难于侵入小孔之中。利用外加压力可以克服表面张力带来的阻力，使液态汞填充到不同大小的气孔之中。迫使汞进入给定大小的孔隙所需的压力，符合拉普拉斯公式：

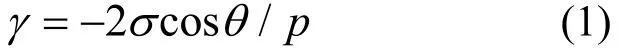
式中，γ为多孔介质孔径；σ为汞的表面张力，常取值为480×10–5N/cm；p为毛细管压力，即压入汞的压力；θ为液固接触角，一般取130°，根据所施加的压力，便可确定出与之相对应的孔径尺寸。由汞的压入量，可测定出气孔体积随孔径变化的曲线。

1.2 孔隙结构分维计算模型

1.2.1 孔径分布分形维数计算模型

由分形几何原理，设砂岩孔隙某一孔径 r，则砂岩中孔径大于r的孔隙数目为N(r)，则有[16]：

式中，D为分维数。

若设V(r)为半径不小于r的孔隙体积，V0为测试样品孔隙总体积，研究表明，V(r)与V0存在关系为(Ki为常数，i=0,1,2,3)：

由式(2)、(3)求导得到：

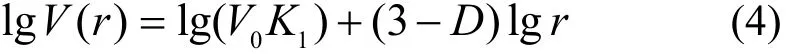
只要在双对数坐标系下绘出 V(r)/V0–r的散点图，并进行线性拟合，根据直线的斜率就可以求得孔隙大小分布的分维数。

1.2.2 孔隙表面分形维数计算模型

与孔隙体积一样，半径不小于r的孔隙的比表面积S(r)与测试样品孔隙总比表面积S0满足：

根据比表面积与尺码的关系取其对数有：

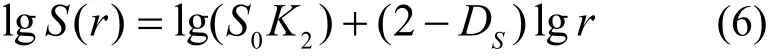
只要在双对数坐标系下绘出 S(r)/S0–r的散点图，并进行线性拟合，根据直线的斜率可以求得孔隙表面的分维数。

2 含铀砂岩孔隙结构特征压汞法研究

2.1 含铀砂岩压汞实验

本次实验压汞仪器为美国 Micromeritrics公司Autopore IV 9510型全自动压汞仪。实验样品来源于某地浸铀矿山钻孔的矿岩样，实验样品选用编号为N126、A202、A204、A307、NK2-1。取部分矿样在高温下烘干至恒重后，在各矿样中分别取少许做每个试样的压汞实验样品。通过对5个矿样的压汞实验，得到压汞曲线特征参数见表1。由表1，矿样中孔隙率与总入汞率、表面密度、平均孔径是成正比关系。孔隙率越大，其总入汞率、表面密度、平均孔径值就越大。

表1 砂岩压汞曲线特征参数Table 1 Characteristic parameters of sandstone for intrusive mercury curve.

2.2 砂岩孔隙分维数的计算及讨论

该地浸铀矿山含矿层铀矿岩孔隙的成因复杂多样。就孔径而言，不同孔径对含矿层的渗透能力的影响不同。根据压汞实验数据，以孔径大小为一有限集，确定孔径大小的上、下限分别为半径2075、0.015 μm。从压汞曲线数据可以看出，孔隙对渗透率影响的有效区间相差很大，故探讨该含矿层矿岩孔隙结构的分形特征。

根据压汞实验，得到入汞压力与总入汞饱和度、孔隙体积累积变化与孔径、孔隙表面积累积变化与孔径等关系，从而得到孔隙分布分形维数与孔隙表面分形维数。分别求得每一样品的孔隙半径与对应的孔隙累积体积V(>r)、孔隙半径与孔隙累积表面积S(>r)和矿样中的汞饱和度SHg与孔隙压力P三组数据对。分别可求出lgV(>r)、lgr、lgS(>r)的值，并在直角坐标系上分别作出lgV(>r)与lgr、lgS(>r)与lgr的散点图，并对其进行线性回归拟合，结果如图1、图2所示。根据前文介绍的孔隙结构分维计算模型，可分别求出各岩样的孔隙分布分维数和孔隙表面分布分维数(表2)。

表2 含铀砂岩孔隙结构分维值Table 2 Fractal dimension value of pore structure in uranium-bearing sandstones.

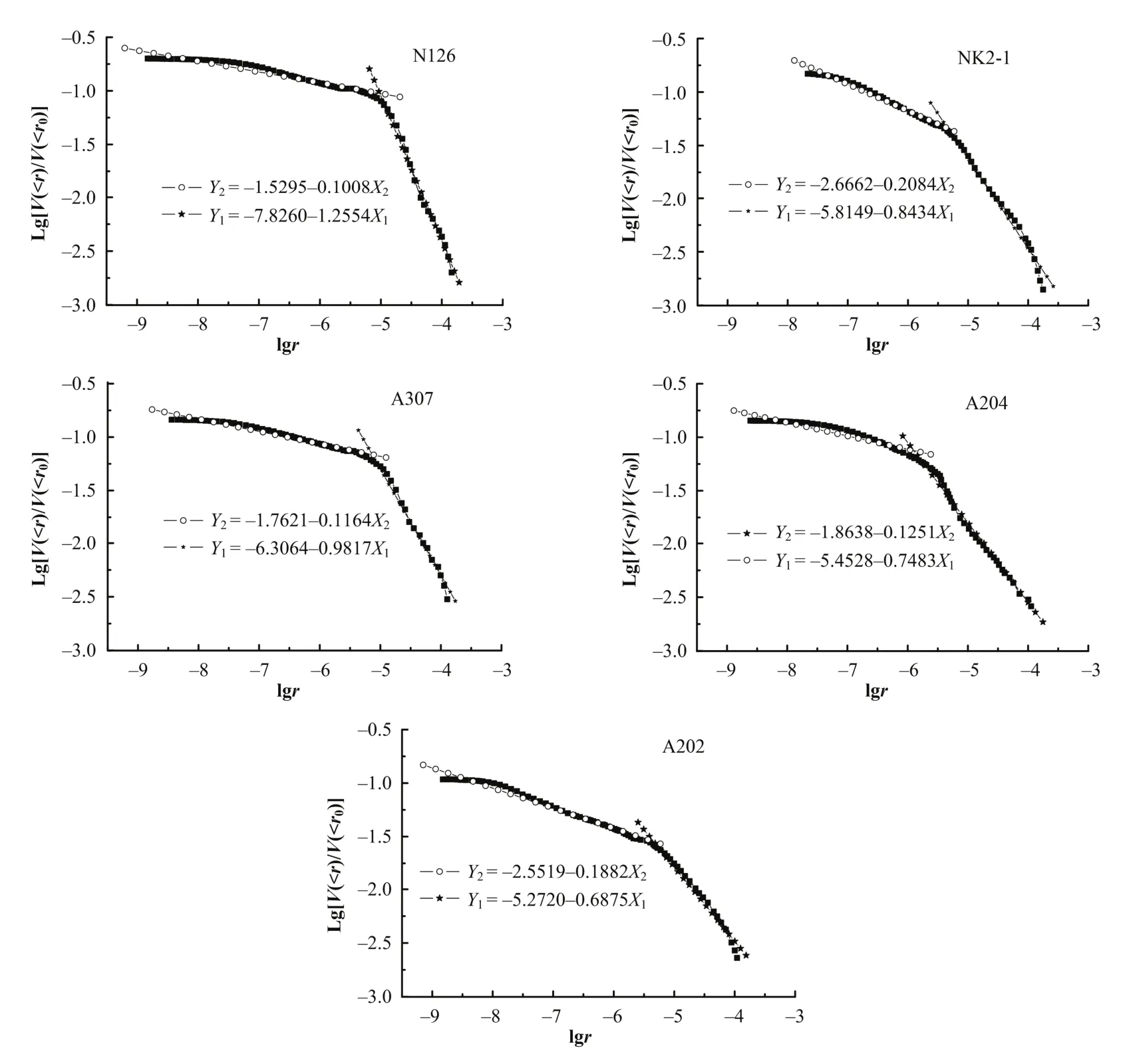
图1 岩样孔隙半径与对应累积体积对数散点图及线性拟合Fig.1 Logarithm scatter diagram and linear fitting for pore radius and corresponding cumulative volume of rock samples.

由图1、2，曲线均有明显的拐点，以拐点散点为界，每个矿样实验散点均能拟合成两条近似直线，两条直线表明该含铀砂岩孔隙结构具有双分形维数的特征，渗透性砂岩铀矿岩结构这种双重分形特征，与文献[17,18]所研究双段幂率现象非常相似。这种双分形维数的特征主要是与砂岩型铀矿床的成矿过程有关系，这与地质资料显示的该铀矿床是通过地质作用与沉积过程两个不同的成矿作用叠加形成的相符合。

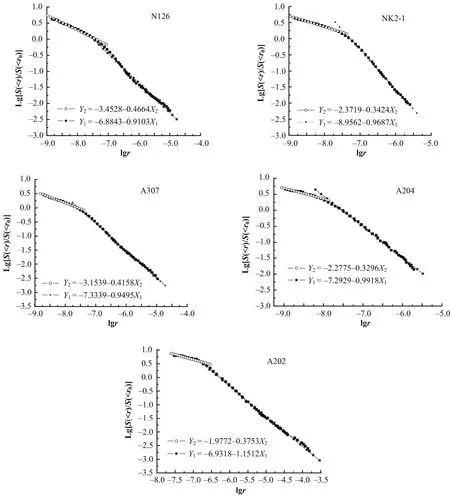
图2 岩样孔隙半径与对应累积比表面积对数散点图及线性拟合Fig.2 Logarithm scatter diagram and linear fitting for pore radius and corresponding cumulative surface area of rock samples.

表2中，Dv1、Dv2分别表示按大、小孔径计算的孔隙体积分维数，Ds1、Ds2分别表示按大、小孔径计算的孔隙比表面分维数。采用压汞曲线数据分析矿岩结构特征时，该地浸铀矿山含铀砂岩样品孔隙结构孔隙分布分维数(以大孔径计算)在4.255−3.687，平均为3.833，而孔隙比表面分维数在3.151−2.910，平均为3.031。而按小孔径计算孔隙体积分维数与孔隙表面分维数各样品基本相同，分别在 3.150与2.400左右。这里所谓的小孔径是指矿样颗粒内部的孔隙，各矿样基本在一个成矿带，矿岩颗粒内部结构基本相同，这样就造成按小孔径计算孔隙结构分维值基本相等。而大孔径指的是颗粒间的孔隙，由于大小颗粒的不同排列造成了各矿样孔隙结构是不同的，主要表现在以大孔径计算出来的分维数。

由图 3，砂岩孔隙结构分形特征与孔隙度之间的关系主要表现为以大孔径孔隙计算出来孔隙与孔隙比表面分维值与孔隙度之间的关系，孔隙率与大孔径计算孔隙分维成正相关关系，与以大孔径计算的孔隙比表面分维成负相关关系。

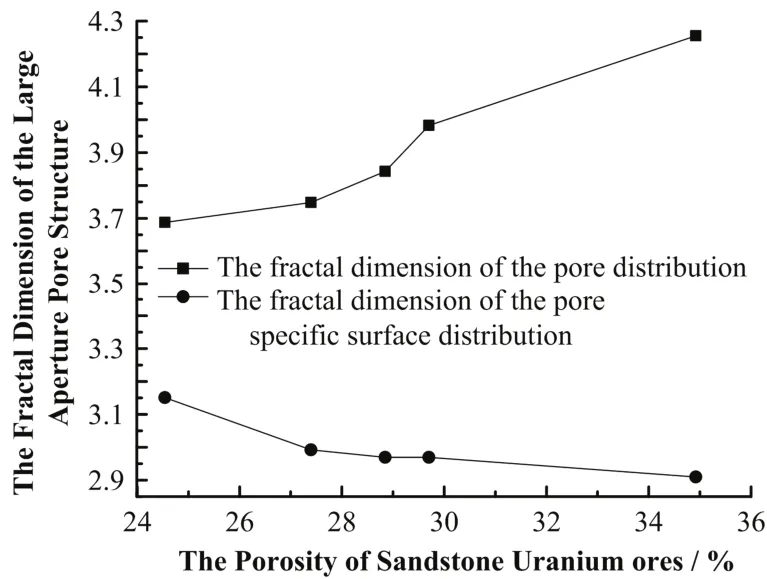
图3 含铀砂岩孔隙结构分形特征与孔隙度的关系Fig.3 The relation between sandstone uranium ore rock pore structure of fractal characteristics and porosity.

3 结语

通过压汞实验对某低渗透性砂岩铀矿岩孔隙结构特征研究，得到如下结论：

(1) 该类型可地浸开采的砂岩铀矿岩孔隙结构具有双分形维数的特征。双重分维数分别是以大、小孔径来计算的。这与砂岩型铀矿床的成矿过程中地质作用与沉积过程两个不同的成矿作用叠加有关。文中所得到的这种渗透性砂岩铀矿岩结构双重分形特征的双段幂率现象，对于双段分形结构的起源，拐点位置等还有待进一步研究。

(2) 以大孔径计算时，各砂岩样品孔隙结构孔隙分布分维数和孔隙比表面分维数变化区间均比以小孔径计算的分维值大。说明该砂岩铀矿岩孔隙结构特征表现为：颗粒间的孔隙分布不很均匀，而颗粒内部的分布比较均匀。

(3) 通过分析砂岩孔隙结构分形特征与孔隙度之间的关系，得到孔隙率与大孔径计算孔隙分维成正相关关系，与以大孔径计算的孔隙比表面分维成负相关关系。

1 赵明, 郁伯铭. 数字岩心孔隙结构的分形表征及渗透率预测[J]. 重庆大学学报, 2011, 34(4): 88−94 ZHAO Ming, YU Boming. The fractal characterization of pore structure for some numerical rocks and prediction of permeabilities [J]. Journal of Chongqing University,2011, 34(4): 88−94

2 姜岩, 雷华阳, 郑刚, 等. 动荷载作用下结构性软土结构变化的分形研究[J]. 岩土学, 2010, 31(10): 3075−3080 JIANG Yan, LEI Huayang, ZHENG Gang, et al. Fractal study of microstructure variation of structured clays under dynamic loading[J]. Rock and Soil Mechanics,2010, 31(10): 3075−3080

3 ZENG Sheng, TAN Kaixuan. Fractal characteristics of po rous structure for in situ leachable sandtone uranium ore[C]. International Mining Forum 2010, 2010, 9: 209−213

4 Christos D. Tsakiroglou, Marios A. Ioannidis, et al. A new approach for the characterization of the pore structure of dual porosity rock[J]. Chemical Engineering Science,2009, 64: 847−859

5 王启立, 胡亚非, 何敏, 等. 石墨多孔介质孔隙度与比表面积的分形描述[J]. 煤炭学报, 2010, 35(10):1725−1729 WANG Qili, HU Yafei, HE Min, et al. Fractal description of porosity and specific surfacearea for porous media of graphite[J]. Journal of China Coal Society, 2010, 35(10):1725−1729

6 倪化勇, 刘希林. 泥石流堆积物的粒度分布及其分形结构[J]. 沉积与特提斯地质, 2008, 28(3): 35−41 NI huayong, LIU Xilin. Grain-size distribution and fractal structures of solid grains in debris-flow deposits[J].Sedimentary Geology and Tethyan Geology,2008, 28(3): 35−41

7 王海峰, 阙为民, 钟平汝, 等. 原地浸出采铀技术与实践[M]. 北京: 原子能出版社, 1998: 8 WANG Haifeng, QUE Weimin, ZHONG Pingru, et al.In-situ leaching uranium mining technology and practice[M]. Beijing: Atomic Energy Press, 1998: 8

8 曾晟. 低渗透性砂岩铀矿床原地浸出的分形动力学研究[D]. 衡阳: 南华大学, 2011 ZENG Sheng. Study on fractal dynamics of in-situ leaching of uranium in low-permeability sandstone uranium deposits[D]. Hengyang: University of South China, 2011

9 阙为民, 王海峰, 牛玉清, 等. 中国铀矿采冶技术发展与展望[J]. 中国工程科学, 2008, 10(3): 44−53 QUE Weimin, WANG Haifeng, NIU Yuqing, et al.Development and prospect of china uranium mining and metallurgy[J]. Engineering Sciences, 2008, 10(3): 44−53

10 廖文胜, 王立民, 苏学斌, 等. 某低渗透砂岩铀矿岩心特性分析[J]. 铀矿冶, 2007, 26(4): 185−190 LIAO Wensheng, WANG Limin, SU Xuebin, et al. Core analysis of a low permeable sandstone uranium deposit[J].Uranium Mining and Metallurgy, 2007, 26(4): 185−190

11 刘志彬, 刘松玉, 居俊, 等. 崇启大桥接线工程下部软土孔隙结构分析[J]. 东南大学学报(自然科学版), 2012,42(3): 531−537 LIU Zhibin, LIU Songyu, JU Jun, et al. Pore structure characteristics analysis of soft soil under connection project of Chongqi Bridge[J]. Journal of Southeast University (Natural Science Edition), 2012, 42(3):531−537

12 马立民, 林承焰, 范梦玮. 基于微观孔隙结构分形特征的定量储层分类与评价[J]. 石油天然气学报, 2012,34(5): 15−20 MA Limin, LIN Chengyan, FAN Mengwei. Quantitative classification and evaluation of reservoirs based on fractal features of micro-pore structures[J]. Journal of Oil and Gas Technology, 2012, 34(5): 15−20

13 邓玉珍, 刘慧卿, 张红玲, 等. 基于孔隙分维数的岩石分类方法[J]. 油气地质与采收率, 2007, 14(5): 23−26 DENG Yuzhen, LIU Huiqing, ZHANG Hongling, et al.Petro-graphic classification method based on porous fractal number[J]. Petroleum Geology and Recovery Efficiency, 2007, 14(5): 23−26

14 马占旗, 任晓娟, 张宁生, 等. 特低渗储层砂岩孔隙结构的分形研究[J]. 新疆石油地质, 2007, 28(1): 88−91 MA Zhanqi, REN Xiaojuan, ZHANG Ningsheng, et al. A fractal study on pore structure of sandstone in extra low permeability reservoirs[J]. Xinjiang Petroleum Geology,2007, 28(1): 88−91

15 唐伟家, 齐志强. 用压汞仪测聚丙烯腈原丝微孔结构[J]. 合成纤维工业, 1983, 6(1): 29−30, 63 TANG Weijia, QI Zhiqiang. Experimental study of pressure mercury for the microporous structure of polyacrylonitrile precursor[J]. China Synthetic Fiber Industry, 1983, 6(1): 29−30, 63

16 马新仿, 张士诚, 朗兆新. 孔隙结构特征参数的分形表征[J]. 油气地质与采收率, 2005, 12(6): 34−36 MA Xinfang, ZHANG Shicheng, LANG Zhaoxin. Fractal characterization of characteristic parameters of pore structure[J]. Petroleum Geology and Recovery Efficiency,2005, 12(6): 34−36

17 钱江海, 韩定定, 马余刚. 开放式复杂航空网络系统的动力学演化[J]. 物理学报, 2011, 60(9): 098901 QIAN Jianghai, HAN Dingding, MA Yugang. Dynamical evolution of complex airline system[J]. Acta Phys Sin,2011, 60(9): 098901

18 Han D D, Qian J H, Ma Y G. Emergence of double scaling in complex systems[J]. Europhysics Letters, 2011, 94:28006