吉林西部气象干旱的多标度分形特征
陈社明,卢文喜,罗建男,康 柱
1.吉林大学地下水资源与环境教育部重点实验室,长春 130021
2.中国建筑材料工业地质勘查中心吉林总队,长春 130033
0 引言
干旱是世界上代价最高的自然灾害,每年在全球能够造成60~80亿美元的经济损失,它所影响的人口数量超过其他任何一种自然灾害[1]。各个部门或学科对干旱概念的定义不尽相同,一般把干旱分为气象干旱、水文干旱、农业干旱和社会经济干旱,气象干旱是其他各类干旱发生的主要原因[2]。
目前,关于气象干旱指标已有大量的研究。根据建立途径的不同可以把干旱指标归纳为2类:一类是通过研究干旱机理,力图细致地反映干旱涉及的各个物理过程,以干旱监测指数(Palmer drought severity index,PDSI)[3]、KBDI(Keetch-Byram drought index)[1]和 WAWAHAMO(Wald Wasser Haushalts Modell)[4]等为代表;另一类则是通过气象学方法研究降水量的统计分布规律,以反映干旱的强度和持续时间,代表性模型是McKee等在评估美国科罗拉多干旱状况时提出的基于降水量的标准化降水指标(standardized precipitation index,SPI)[5]。由于SPI能够非常好地反映干旱的强度和持续时间,同时具有多时间尺度应用的特性,使得用同一个干旱指标反映不同时间尺度和不同方面的水资源状况成为可能,因而得到广泛应用[6]。
相对于干旱指标来说,国内外对干旱分析方法的研究还比较薄弱,当前的研究方法主要集中在游程理论、随机模拟及非参数方法[7]。由于干旱可以视作时间轴上的点状事件,所以干旱灾害的发生十分类似于典型的康托尔集(cantor),即局部与整体之间在一定标度域内具有自相似特征[8]。从数学的角度讲,自相似性意味着标度不变性[9]。20世纪70年代兴起的分形理论能够将不同尺度下的水文变量通过标度变换联系起来,因此运用分形的理论和方法,对不同尺度下干旱的变化规律进行研究,具有重要的理论意义和实用价值。目前,分形理论已经在我国多个地区的干旱特征分析中被应用:冯平等[10]介绍了分形理论的基本概念及其分维值的计算方法,探讨了干旱要素在一定标度范围内的统计时间分形特征;朱晓华等[11]基于分形理论对中国旱涝灾害研究方面所存在的问题进行了分析;郭毅等[12]采用标度变换法对陇中地区1368-1948年(明代至新中国建立前)各等级干旱灾害及旱季序列的时间分维值进行测算,并深入讨论了各旱灾序列时间分维与其线性特征之间的关系。上述研究均侧重于运用单重分形理论对干旱的分维值进行计算。然而,在实际研究中,人们发现自然界的分形结构是极其复杂的,仅用一个分形维数来描述其精细结构是不够的。为了准确反映这种复杂性,人们引入了多重分形的概念,多重分形也称作多标度分形。
笔者以标准化降水指数作为气象干旱指标,通过引入多标度分析理论,运用乘法级联模型对吉林西部地区气象干旱的标度性质进行研究,了解其空间分布特征,以期为有效的干旱预测提供帮助,为干旱的研究提供新的途径。
1 数据来源
吉林西部地区位于我国湿润的东部季风区和干旱内陆之间的过渡带,为半干旱半湿润的大陆季风气候区。干旱是这一地区的主要气候特征,部分区域干旱几乎年年发生[13]。为了研究气象干旱的标度特征,本次研究共收集到研究区内6个气象站点1957年1月-2010年10月的月降水量数据。数据来自于中国气象科学数据共享服务网。6个站点的位置及其降水量序列见图1,各站点降水统计结果见表1。
2 研究方法
2.1 标准化降水指数
McKee等1993年提出了标准化降水指数(SPI),用来确定有降水量记录地区特定时间尺度的降水异常事件,其时空尺度反映区域不同持续时间的水资源特征[14]。SPI是根据降水量的概率分布计算累积概率,然后再转化成标准正态分布。该指数具有优良的计算稳定的特性。根据Guttman等[15]提出的计算SPI过程,第一步是寻找能够描述降水随不同尺度分布的概率密度函数。在降水分析中,常采用伽马函数作为概率密度函数,其概率分布为Γ分布,具体的计算过程见文献[16]。
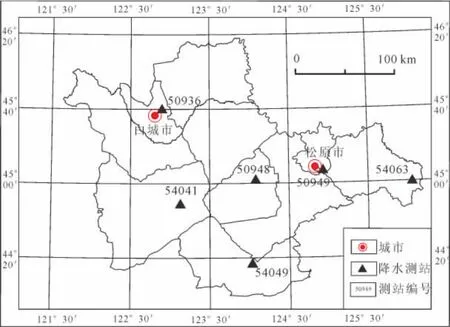
图1 研究区范围及降水量测站位置Fig.1 Location of study area and precipitation stations
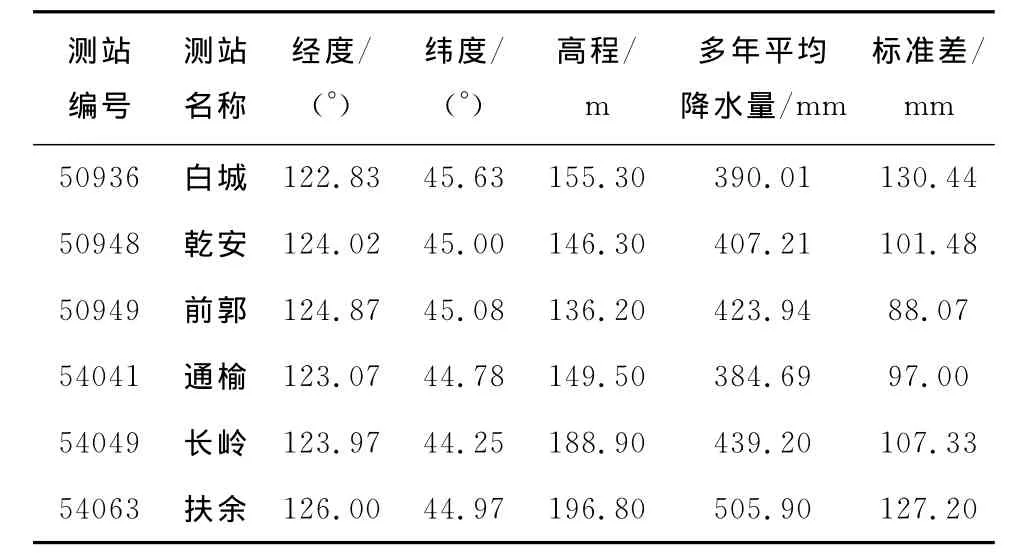
表1 研究区各气象站点基本特征Table1 Meteorological stations used in this study and their basic properties
根据SPI的大小,干旱可以分为4个等级。轻度干旱为-0.99~<0;中度干旱范围为-1.49~<-0.99;严重干旱范围为-1.99~<-1.49;<-1.99为极端干旱。
2.2 多标度分形理论
定义随机变量Yx,脚标x为测量的尺度。根据分形理论,如果对任一个常数λ>0,设Yλx为与尺度λx对应的随机变量,若存在一个关于λ的函数Cλ=λθ使

则称Y满足标度不变性,或具有标度性质。其中:P为概率;θ称为标度指数。θ可为与P无关的常数,此时称为单标度;也可与P有关,此时称为多标度[17]。
笔者通过分析不同尺度下干旱时间(负SPI月数)来分析各站点的标度性质。首先将负的SPI序列以时间尺度s分为相互不重叠的N 个时段。对不同的尺度s,分别计算各个时段内的干旱月数F(s,i);然后计算F(s,i)的q阶矩,并对i求和,得到统计矩K(s,q):
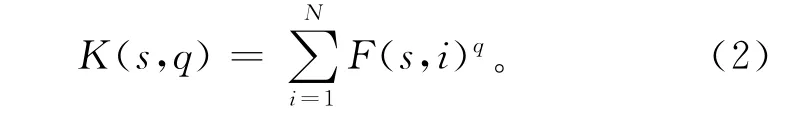
式中:N 是时段数,与研究时段长度有关;F(s,i)为时间尺度s下,i时段的干旱月数;s为时间尺度,月;q是阶数,一般取值范围在0到4之间。对于具有标度性质的变量,统计矩K(s,q)可以用尺度s和标度指数τ(q)来表示[18]:
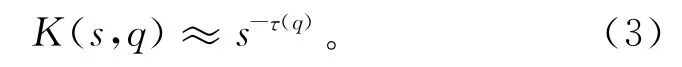
如果τ(q)为阶数q的线性函数,则数据序列称为单标度分形;若为非线性函数,则称为多标度分形。当数据为多标度分形时,需要一个能够描述τ(q)与q关系的函数形式。Over和 Gupta[19]提出的倍增串级模型能够很好地反映两者间的相互关系。因此,笔者采用文献[19]中介绍的β-对数正态串级模型进行拟合,其具体形式如下:
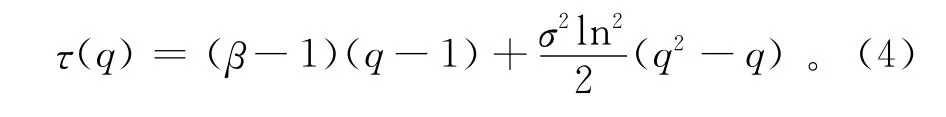
式中,参数β和σ是拟合参数。其中:β表示数据的间歇程度(0≤β≤1);σ2用来量化数据的标度特征(σ≥0),σ2越大表明多标度分形越明显。因此,研究区干旱的多尺度特征分析,主要是计算参数σ2的大小。
3 计算结果的分析与讨论
3.1 标准化降水指数的计算结果分析
根据研究区6个站点1957年1月-2010年12月的月降水资料,利用Visual Basic语言编制的计算程序包,计算出各站点的月SPI序列。为了验证计算结果的稳定性,以扶余站为例,将该站点10月份和5月份的降水量从小到大进行排序,并在表2中列出了降水量和SPI值排序前10的年份。根据表2数据对比可以看出,SPI较好地体现了降水量大小的变化趋势,也反映了干旱程度的强弱。
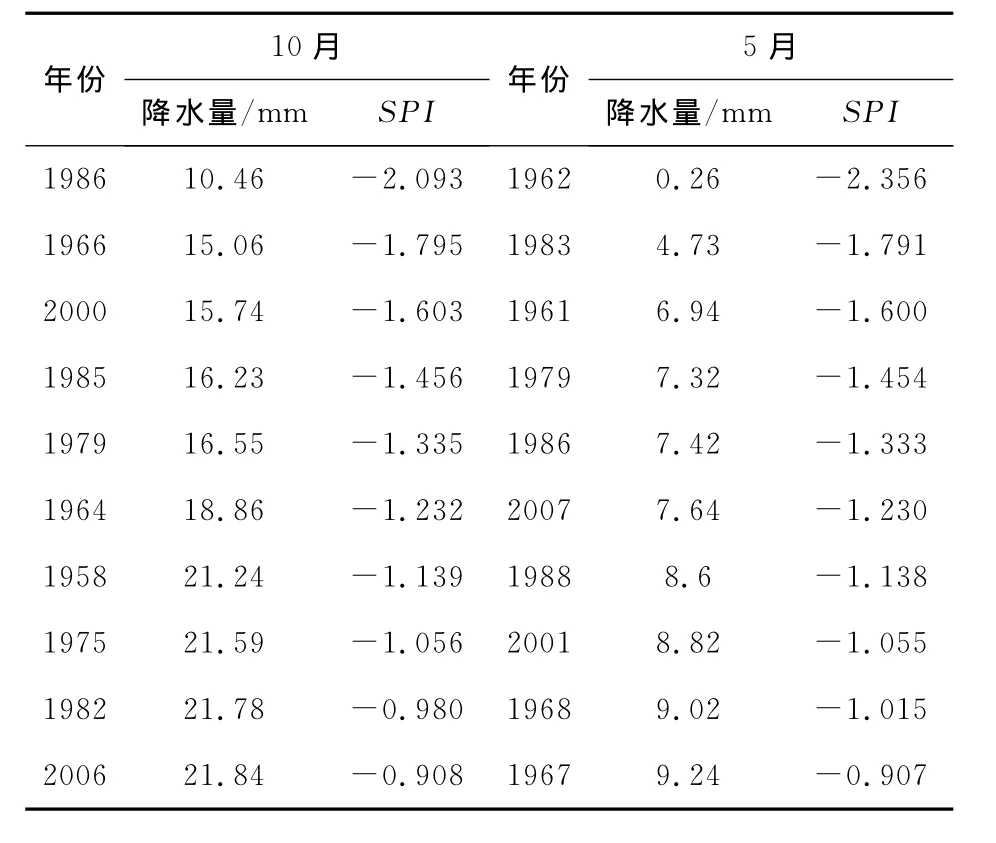
表2 扶余站部分年份10月和5月降水量和SPI值排序结果Table2 Precipitation and SPI values for the October and May partial years in Fuyu station
由于本次主要研究干旱问题,因此,在分析中根据干旱分级表,只考虑月SPI为负数的月份。根据月SPI值大小,对研究时间段内不同等级干旱发生的月份数进行统计,从而了解不同站点干旱程度,统计结果见表3。由表3中看出:在相同的研究时段内,各个站点总的干旱月数近似相等,其中白城的干旱月数最多,为326个月;极端干旱中,通榆和长岭月数最多,为14个月;严重干旱中,乾安月数最多,为25个月。
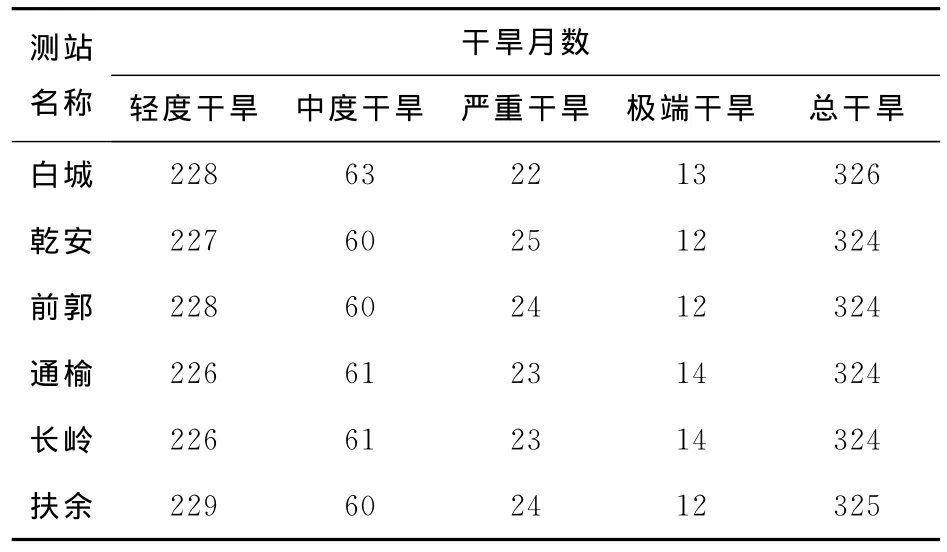
表3 不同干旱级别的月干旱统计结果Table3 Statistical results for monthly drought in different drought categories
3.2 干旱的标度性质分析
描述研究区各站点干旱的标度性质步骤如下:1)将以上计算得到的各站点SPI序列,去除正值后得到新的干旱序列。2)以不同的时间尺度s(s=4i,i=1,2,…,8)为单位,在整个统计时间域上划分互不重叠的N个时段,计算各个时段内干旱月数并计算其q阶矩,将计算结果代入公式(3)得到统计矩K(s,q)。3)将各站点统计矩 K(s,q)和不同阶数s绘制在双对数坐标中,确定不同阶数下阶矩与尺度曲线的斜率;当阶数为q时,根据公式(3)可以看出斜率的大小对应标度指数τ(q);用β-对数正态串级模型拟合系列的q和τ(q)点,并用相关系数的平方来衡量拟合效果。4)根据拟合最好的曲线,确定β和σ2。
由图2可以看出,在不同阶距下,统计矩K(s,q)与尺度s在双对数坐标内呈线性关系,说明各气象站点气象干旱具有标度性质。根据不同阶数q对应的斜率,可以计算出一系列的τ(q)-q散点,将各离散点绘制在平面坐标内,见图3中圆点。根据散点分布可以看出τ(q)与q不是一条直线。因此,各站点干旱的发生在时间尺度上可以视为具有多标度分形特征。将β-对数正态串级模型计算的曲线与观察数据进行拟合。选取回归系数(R)平方最大时对应的β及σ2作为最终计算结果(表4)。

图2 各站点0~4阶统计矩与尺度的双对数关系图Fig.2 Double-logarithmic relationship diagram with statistical moments of 0-4order with the scale in all stations
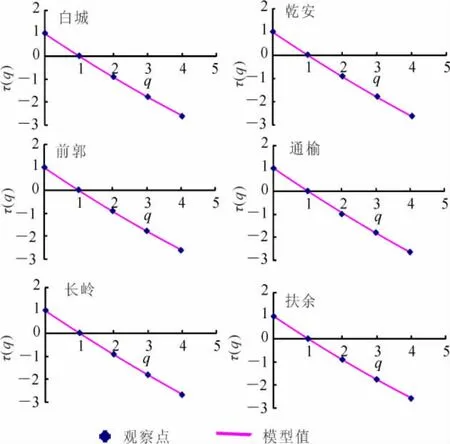
图3 各站点标度指数与阶数的拟合曲线Fig.3 Fitting curve with the scaling exponent and the order in all stations
从表4看出,σ2范围从0.056 9到0.077 4,β范围从0.016 4到0.034 5。σ2在各站点均不为0,这说明研究区内各站点的干旱具有多标度分形特征。依据参数σ2的大小,各站点多标度分形特征的强弱排序为:长岭<通榆<白城<前郭<扶余<乾安。其中,乾安多标度分形特征最强,长岭多标度分形最弱。
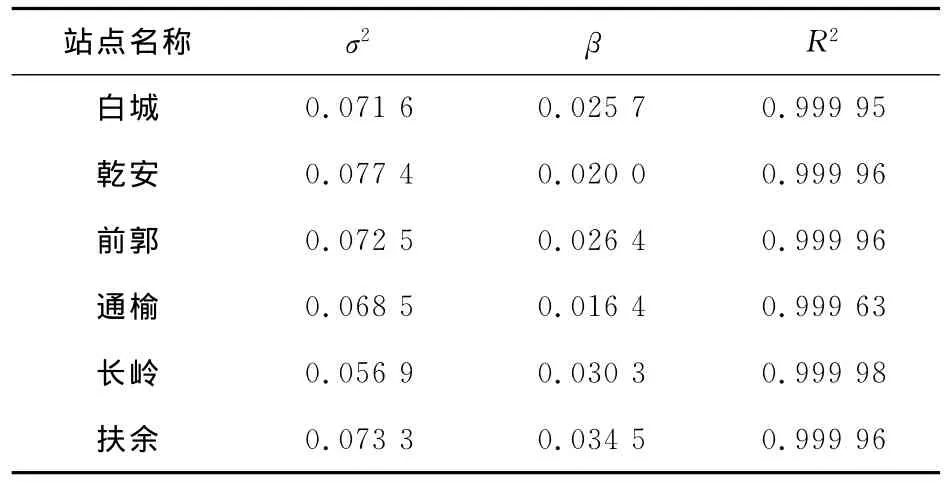
表4 各站点多标度分形参数的拟合结果Table4 Fitting results of multifractal parameters in all stations
旱涝的发生在时间上表现为不连续的点过程,它不是简单的直线,亦非可微分的曲线,而且从周期的角度出发,不同时间跨度的周期相互嵌套,长周期中包含短周期,短周期中又有更短的周期[10]。干旱的发生存在多时间尺度特征。在所受影响因素越复杂的地区,其干旱的多时间尺度越明显,分布的层次结构越复杂,相应的多标度分形特征就越明显[20]。因此,研究区不同站点多标度分形特征在空间上的强弱不同,反映了各地区不同尺度或者周期气候条件对干旱在时间上的影响。
根据前人研究结果,干旱的物理成因不仅与大气圈有关,而且与水圈、岩石圈、生物圈、冰雪圈有关,其中大气圈和水圈关系最为密切;其次与陆面过程有关,生物过程影响最小[21]。考虑研究区6个站点所处的大气候条件相似,海拔高程也相差不大,因此,引起干旱多重分形特征不同的主要因素为海洋和陆地的热状况的影响,如具有一定周期特征的厄尔尼诺、南方涛动等中尺度气候活动的影响。对于干旱趋向于单标度特征的站点,干旱的发生受这种中尺度气候的影响较为强烈和持续,表现出显著的周期性;相反,对于趋向多标度特征的站点,干旱的发生受这种气候的影响相对较弱,从而导致干旱没有显著的周期。显然,研究区内扶余和乾安干旱的多标度分形特征更加明显,长岭和通榆则趋向于单标度分形。趋向于单标度分形也就意味着干旱的发生具有一致性,随尺度不同,干旱发生有规律的变动。多标度性质越明显意味着干旱的发生受到的影响因素比较复杂,干旱发生的周期性不断发生变化。
干旱的多重分形特征分析可为干旱的研究提供新的途径,其分析结果有助于区分不同地区干旱特征在空间尺度上的差异性,为干旱预测模型的参数推断提供参考。同时,分析结果还能够指导不同地区干旱的分维值计算,评价哪些地区需要用多个分维值来反映干旱的分形特征。
4 结论
1)根据标准化降水指数(SPI)的计算过程了解到,利用SPI作为干旱指数具有计算简单、资料容易获取、计算结果稳定的特点。通过对研究区内6个气象站点1957年1月-2010年10月标准化降水指数的计算和分析表明,乾安县发生的严重干旱月数最多,通榆和长岭发生极端干旱的月数最多。
2)吉林西部气象干旱的发生在时间尺度上均具有多标度分形特征,但在不同站点多标度分形的强度不同,表现出一定的空间差异性。其强弱次序为:长岭<通榆<白城<前郭<扶余<乾安。
3)由于多标度分形能够反映时间序列的奇异性,越复杂的事物,分布的层次结构越复杂,其多标度分形特征就越明显。研究区不同站点多标度分形特征在空间上的强弱不同,反映了各地区不同尺度或者周期气候条件对干旱在时间上的影响。越趋向于多标度说明其干旱发生的规律性越弱,越趋向于单标度说明其干旱发生的规律性越强。
(Reference):
[1]Byun H R,Wilhite D A.Objective Quantification of Drought Severity and Duration[J].J Climate,1999,12(9):2747-2756.
[2]王劲松,郭江勇,周跃武,等.干旱指标研究的进展与展望[J].干旱区地理,2007,30(1):61-67.Wang Jinsong,Guo Jiangyong,Zhou Yuewu,et al.Progress and Prospect on Drought Indices Research[J].Arid Land Geography,2007,30(1):61-67.
[3]Palmer W C,Bureau E U W.Meteorological Drought[M].Washington:US Dept of Commerce,1965.
[4]Zierl B.A Water Balance Model to Simulate Drought in Forested Ecosystems and Its Application to the Entire Forested Area in Switzerland[J].Journal of Hydrology,2001,242(1/2):115-136.
[5]McKee T B,Doesken N J,Kleist J.The Relationship of Drought Frequency and Duration to Time Scales[C]//Proc 8th Conference on Applied Climatogy.Anaheim:American Meteorological Society,1993.
[6]Giddings L,Soto M,Rutherford B,et al.Standardized Precipitation Index Zones for México[J].Atmósfera,2005,18(1):33-56.
[7]闫宝伟,郭生练,肖义,等.基于两变量联合分布的干旱特征分析[J].干旱区研究,2007,24(4):537-542.Yan Baowei,Guo Shenglian ,Xiao Yi,et al.Analysis on Drought Characteristics Based on Bivariate Joint Distribution[J].Arid Zone Research,2007,24(4):537-542.
[8]丁贤法,李巧媛,胡国贤.云南省近500年旱涝灾害时间序列的分形研究[J].灾害学,2010,25(2):76-80.Ding Xianfa,Li Qiaoyuan,Hu Guoxian.Fractal Study on Time Series of Drought and Flood Disasters of the Recent 500Years in Yunnan Province[J].Journal of Catastrophology,2010,25(2):76-80.
[9]常福宣.分形理论在水文水资源研究中的应用[D].成都:四川大学,2001.Chang Fuxuan.The Applications of Fractal Theory in the Study of Hydrology and Water Resources[D].Chengdu:Sichuan University,2001.
[10]冯平,王仁超.水文干旱的时间分形特征探讨[J].水利水电技术,1997,28(11):48-51.Feng Ping,Wang Renchao.Investigation on the Time Fractal of Hydrologic Drought[J]. Water Resources and Hydropower Engineering,1997,28(11):48-51.
[11]朱晓华,蔡运龙,王建.中国旱涝灾害的分形结构[J].地球科学进展,2003,18(4):509-514.Zhu Xiaohua,Cai Yunlong,Wang Jian.On Fractal Characters of Drought and Flood of China[J].Advances in Earth Science,2003,18(4):509-514.
[12]郭毅,赵景波.1368-1948年陇中地区干旱灾害时间序列分形特征研究[J].地球科学进展,2010,25(6):630-637.Guo Yi,Zhao Jingbo.Characteristics of Fractal Dimension of Drought Disaster Sequences from 1368 to 1948in Longzhong Area[J].Advances in Earth Science,2010,25(6):630-637.
[13]王鹏文,王国琴,杨双.吉林省西部地区干旱特征分析[J].吉林农业科学,1991(4):90-94.Wang Pengwen,Wang Guoqin,Yang Shuang.An Analysis of Dry Climatological Feature in the West of Jinlin Province[J].Journal of Jilin Agricultural Sciences,1991(4):90-94.
[14]谭学志,粟晓玲,邵东国.基于SPI的陕西关中地区气象干旱时空特征分析[J].干旱地区农业研究,2011,29(2):224-229.Tan Xuezhi,Su Xiaoling,Shao Dongguo.Analysis of Spatial and Temporal Characteristics ofMeteorological Drought in Guanzhong Region of Shaanxi Province[J].Agricultural Research in the Arid Areas,2011,29(2):224-229.
[15]Chortaria C,Karavitis A,Alexandris S.Development of the SPI Drought Index for Greece Using Geo-Statistical Methods[C]//Marc Morell.Water Observation and Information System for Balkan Countries.Ohrid:Republic of Macedonia,2010.
[16]袁文平,周广胜.标准化降水指标与Z指数在我国应用的对比分析[J].植物生态学报,2004,28(4):523-529.Yuan Wenping, Zhou Guangsheng. Comparison Between Standardized Precipitation Index and Z-Index in China[J].Acta Phytoecologica Sinica,2004,28(4):523-529.
[17]谢淑云,鲍征宇.矩分析法及其在粤北韶关地区金属成矿作用研究中的应用[J].吉林大学学报:地球科学版,2003,33(4):443-447.Xie Shuyun,Bao Zhengyu.The Method of Moments and Its Application to the Study of Mineralization in Shaoguan District,North Guangdong,China[J].Journal of Jilin University:Earth Science Edition,2003,33(4):443-447.
[18]Over T M.Modeling Space-Time Rainfall at the Mesoscale Using Random Cascades[D].Colorado:University of Colorado,1995.
[19]Over T M,Gupta V K.Statistical Analysis of Mesoscale Rainfall:Dependence of a Random Cascade Generator on Large-Scale Forcing[J].Journal of Applied Meteorology,1994,33:1526-1542.
[20]李昭阳,汤洁,孙平安,等.松嫩平原西南部土地利用动态变化的分形研究[J].吉林大学学报:地球科学版,2006,36(2):250-258.Li Zhaoyang,Tang Jie,Sun Ping’an,et al.Fractal Research on Dynamic Change of Land Resources in Southwest of Songnen Plain[J].Journal of Jilin University:Earth Science Edition,2006,36(2):250-258.
[21]李玉中,程延年,安顺清.北方地区干旱规律及抗旱综合技术[M].北京:中国农业科学技术出版社,2003.Li Yuzhong,Cheng Yannian,An Shunqing.Drought Law and Drought Resistance Composite Technology in Northern China[M].Beijing:China Agricultural Science and Technology Press,2003.

