MT有限元模拟中截断边界的影响
汤井田,薛 帅
中南大学地球科学与信息物理学院,长沙 410083
0 引言
国内外学者很早就进行了大地电磁场的数值模拟研究。1971年Coggon[1]首先提出将有限单元法应用在电磁法数值模拟中,并详细阐述了模拟大地电磁场的有限元格式。有限单元法作为一种便捷通用的数值分析方法,相较于有限差分法和积分方程法,具有易于拟合复杂结构、易于对复杂介质目标建模、程序通用性强等优势,从而被迅速广泛地应用于电磁场的数值模拟中。国外学者Rijo[2]、Wannamaker等[3-4]分别对电磁场的有限元模拟进行了发展和完善,Wannamaker等[3-4]将有限元中的矩形网格继续剖分为4个三角形网格,可以更好地模拟地形和地下构造,提高了数值计算精度。在国内,1981年,陈乐寿[4]首先详细介绍了有限元在大地电磁场正演计算中的应用,并利用矩形-三角形网格剖分对有限元模拟大地电磁进行了改进。之后胡建德等[6]、徐世浙等[7]、杨长福[8]、陈小斌[9]分别对地球物理场中的有限单元法进行了研究和发展,至今,有限单元法已经成为二维和三维大地电磁数值模拟的主要手段。
在利用有限元方法模拟二维和三维大地电磁场时,电磁场正演计算时的一些边界条件需要在“无穷远处”才能够满足。而有限元的模拟区域是有限的,所以网格边界处存在截断边界影响。在有限元模拟大地电磁场时,为了避免截断边界的影响,一般将网格边界放在距离研究区域外很远处,如 Rijo[2]、Wannamaker[3-4]、陈乐寿等[10]、徐世浙[11]、赵广茂等[12]、刘长生等[13]在进行大地电磁有限元数值模拟时网格边界都放在足够远处来满足边界条件。但是“足够远距离”一直没有适当的参考值,网格边界选择小了会影响计算精度,而选择过大则需要较高的内存和付出较长的计算时间。Sharma等[14]曾利用趋肤深度δ来进行网格剖分和划分网格边界,认为将网格边界设置在5δ处时即可忽略截断边界的影响,但是没有进行相应的研究说明。作者利用有限元二维大地电磁正演程序,计算总结出适合有限元大地电磁模拟的参考网格边界。
1 边界条件和截断边界
假定地下电性结构为二维结构,选取右旋直角坐标系的原点在地面上,z轴正方向垂直向下,x轴的方向平行于走向方向,即介质的电性参数仅与y、z方向有关。根据麦克斯韦方程,二维地电结构下的大地电磁满足以下二式,称之为亥娒霍兹方程式[10]:
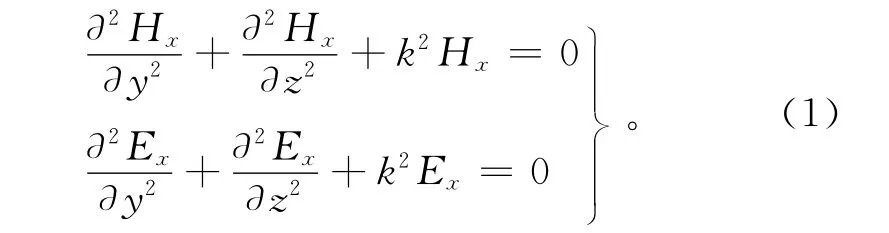
其中:Hx和Ex是x 方向磁场和电场;k2=iωμσ;ω是角频率;μ是导磁率;σ是导电率。
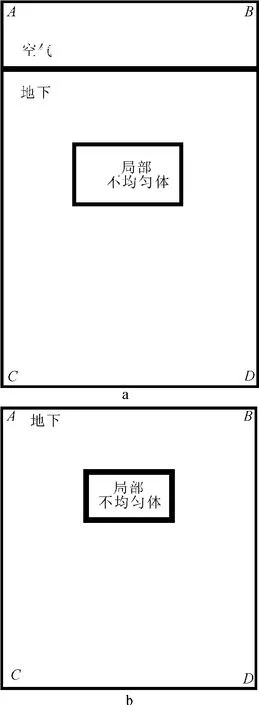
图1 E型波(a)和 H型波(b)的研究区域[11]Fig.1 Research area of E type wave(a)and H type wave(b)[11]
边界如图1所示,设u为需要求解的电磁场,在上边界AB处,电磁场满足第一类边界条件;值得注意的是,TE(transverse electric)模式的上边界要离开地面一段距离。在左右边界AD和BC处,要求由横向不均匀体引起的二次场为0。为此,有2种方式的边界条件加载[10]:一种是强加边界条件,即计算出水平层状介质中的电磁场分布来给出边界上的值;另一种是采用齐次的第二类边界条件,即在侧边界上的场分量u的法向导数为零。一般采用后一种方式作为侧边界的边界条件。而下边界CD处以下被认为是均质岩石,要求局部异常体在CD上的异常场为0。所以u满足的边界条件为

当地下存在不均匀体时,网格边界需要在足够远处才能够满足电磁场的边界条件。
2 截断边界研究
由于在利用大地电磁(magnetotellurics,MT)有限元正演程序进行大地电磁数值模拟时,网格剖分会对计算结果产生很大的影响,所以在进行截断边界研究时,要先避免因网格剖分而造成的计算结果差异。笔者为确保计算结果的正确与可靠,在横向上(y方向)-1 000~1 000m、纵向上(z方向)0~2 000m,按照10m的网格间距进行剖分;而在该研究区域以外,无论横向还是纵向的网格间距,皆按1.1倍率进行增长剖分。对于TE模式参照Wannamaker等[3-4]在PW2D中的作法,以总网格横向距离的一半作为上网格边界的距离。
数值模拟时,在不改变网格剖分的情况下,只对外网格边界进行扩大和减小,从而避免网格剖分的影响。根据电磁场理论,某一频率的电磁场在该频点的一个趋肤深度内迅速衰减至1/e,并在传播中继续衰减至0;因此,笔者以某一频点的趋肤深度作为该频点网格边界选择的量度:
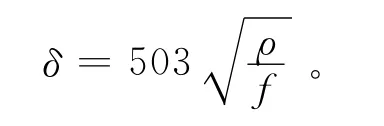
式中:δ为趋肤深度;ρ为电阻率;f为频率。可见,δ与f相关。为了体现普遍性,在MT仪器常用的4个频段中分别选择一个频率作为研究频率,即0.25、2.50、25.00、250.00Hz。
在模型选择上,笔者分别对一维模型(均匀半空间模型和层状介质模型)和二维地电模型进行模拟计算。在进行数值模拟前,将2个方向的网格边界分别放在20倍的趋肤深度距离处,计算出一组数据作为参考解,认为该参考解是在“足够远”的网格边界条件下计算的较精确的数值解。
2.1 一维模型模拟
首先对电阻率为100Ω·m的均匀半空间模型进行模拟计算,分别计算左右网格边界和下网格边界同时为100m和同时为500m的情况,计算结果如表1。
再建立一个层状介质模型(图2),分别计算左右网格边界和下网格边界同时为500m和同时为1 000m情况下的视电阻率,结果如表2所示。

表1 均匀半空间视电阻率计算结果Table1 Apparent resistivity results of homogenous half space

表2 H型层状介质视电阻率计算结果Table2 Apparent resistivity results of layered medium model
在一维模型中不存在局部异常体,自然满足有限元模拟的外边界条件。通过对以上2个模型的计算,进一步说明了在一维有限元数值模拟时边界条件自然满足,不存在截断边界影响,从而无需进行网格边界的扩展。

图2 层状介质模型Fig.2 Layered medium model
2.2 二维地电模型
有限元模拟地下存在二度体的二维地电模型时,由于局部不均匀体的存在,不合适的网格边界会产生较大的误差。对模型2D-1(图3)进行模拟计算,设置左右网格边界和下网格边界均为500m,分别在O点和B点进行观测,表3是O点观测结果。
从表3中可以看出,不合适的网格边界对计算结果影响较大。因此,对二维地电模型进行有限元模拟时,需要选择合适的网格边界。
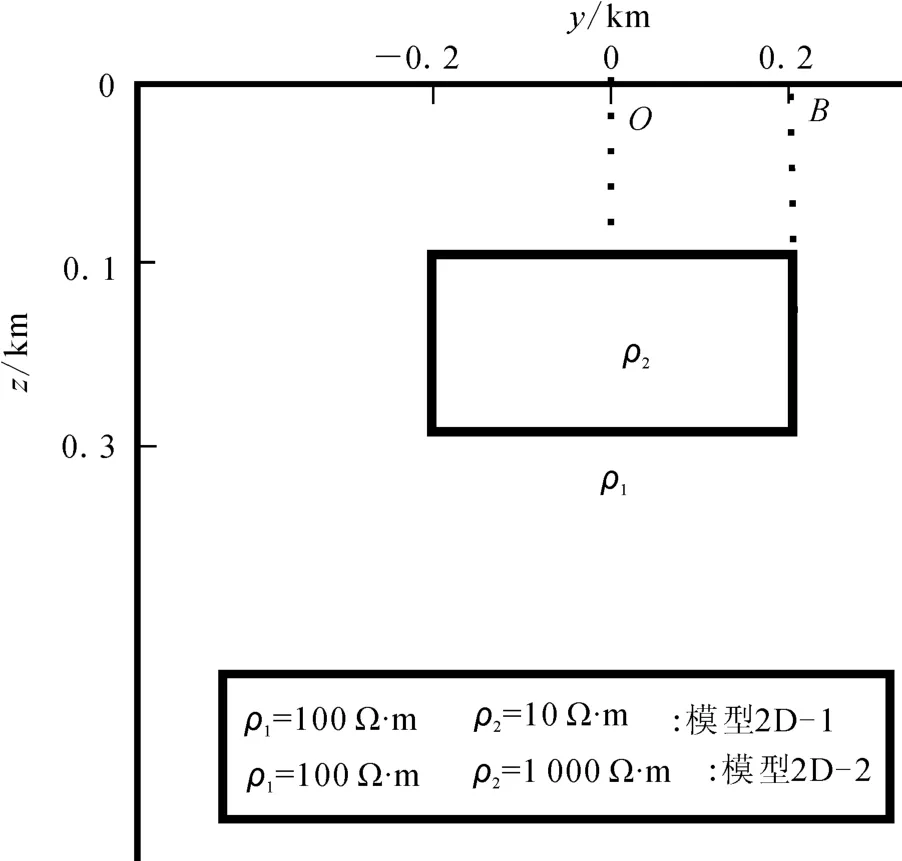
图3 二维地电模型Fig.3 Two-dimensional geoeletric model
根据所选频率和模型电阻率,将下网格边界设置在“足够远”的距离,放在200 000m的地方,计算趋肤深度作为变化量度来改变左右网格边界的边界距离,将计算结果与参考解进行比较。同时约定下网格边界以地下异常体的下边界为基准进行扩展,左右网格边界以异常体的左右边界为基准进行扩展。约定计算趋肤深度时的电阻率为地下电性结构中电阻率最高者。
对背景介质中存在低阻异常体和高阻异常体2种模型进行模拟计算,并在二度体中心上方O点和边界上方B点同时进行TE模式和TM(transverse magnetic)模式观测。
2.2.1 左右网格边界变化

表3 模型2D-1在O点观测结果Table3 Observed results of model 2D-1on point O
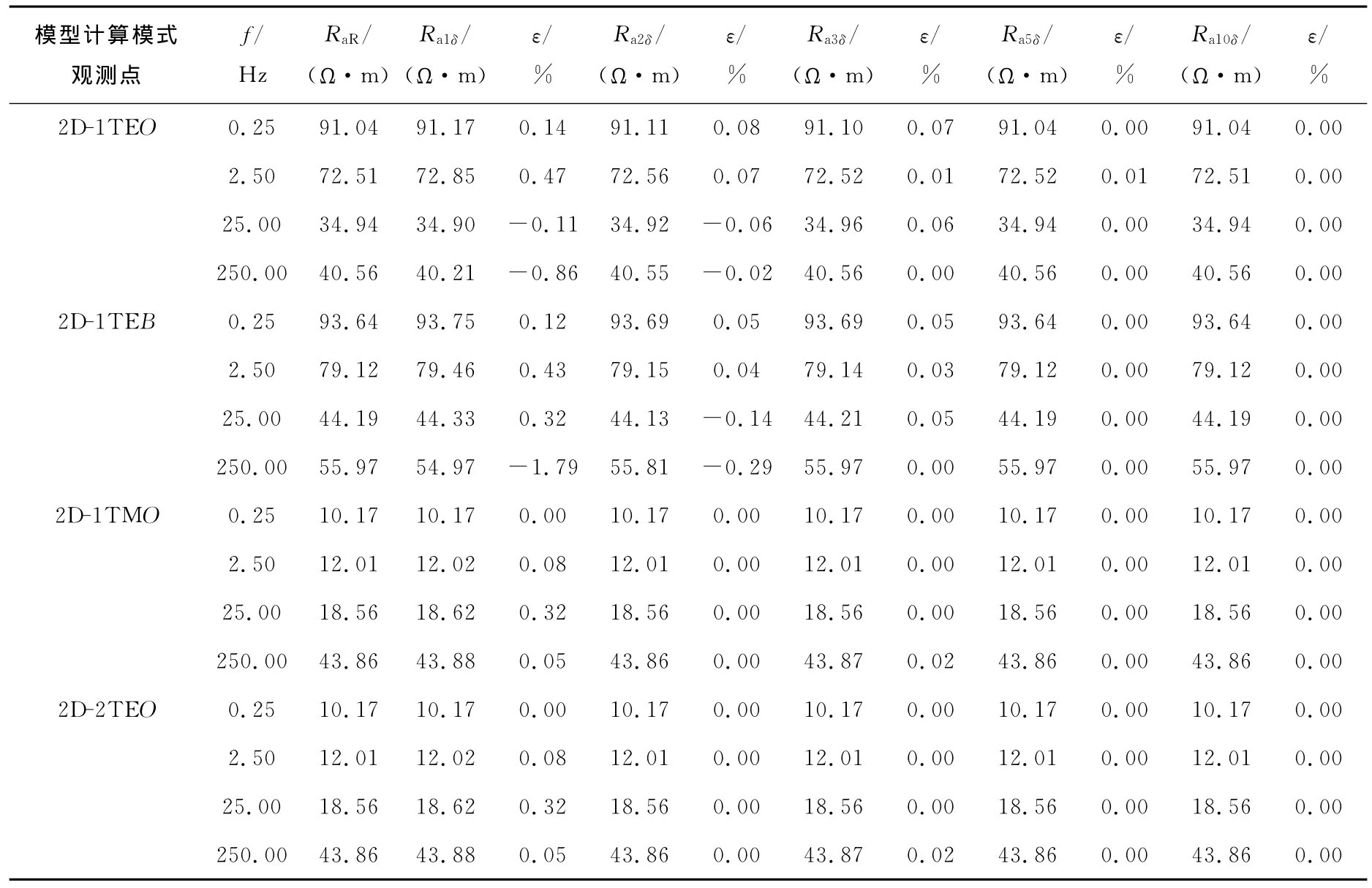
表4 左右网格边界变化下视电阻率观测结果Table4 Apparent resistivity results when changing left and right mesh boundary
从表4可看出:对于模型2D-1,TE模式在1δ网格边界时,O点和B点观测结果的相对误差除250Hz外大部降至1%以下;在2δ的网格边界时,O点观测结果的相对误差已全降至0.1%以下,B点虽相对于1δ网格边界条件时的相对误差有所减小,但部分频率的误差仍在0.1%数量级上;继续增大网格边界至3δ时,O点和B点观测的相对误差已全部降至0.1%以下;继续加大网格边界至5δ和10δ,观测结果与参考结果相等,误差为0。
对于TM模式:在1δ网格边界时,计算的结果相对误差全部在1%以下;增大到2δ网格边界时,相对误差大部为0;继续加大网格边界,相对误差保持为0。对于模型2D-2,在1δ网格边界时,大部分计算结果与参考解相等,相对误差为0。
值得注意的是,对模型2D-2进行模拟时,网格边界变化的量度采用的趋肤深度已相当于模型2D-1的3倍。
2.2.2 下网格边界变化
在对下边界研究时,则把左右网格边界设置在“足够远”的距离,以趋肤深度作为量度来改变下网格边界的边界距离,计算结果并与参考解进行比较。仍然以模型2D-1和模型2D-2为计算模型。模型2D-1的部分计算结果如表5。
从表5中看出:根据TE模式计算结果,在1δ网格边界时,O点和B点观测结果的相对误差已全部降至1%以下;在2δ网格边界时,相对误差继续减小,但大部仍在0.1%的数量级上;继续增大网格边界至3δ时,O点和B点观测的相对误差已全部降至0.1%以下;加大边界至5δ和10δ,观测结果与参考结果相等,误差为0。
对于TM模式:在1δ网格边界时,计算的结果相对误差大部在1%以下;增大到2δ网格边界时,除B点观测的25Hz和250Hz外,大部分结果的相对误差降至0.1%以下;继续增大网格边界,误差继续减少直至为0。
对于下网格边界变化下的高阻模型2D-2,计算的结果与对应的左右网格边界的变化结果相似。即在1δ时,大部分计算结果已与参考解相等,相对误差为0。
3 截断边界选择
3.1 综合网格边界计算
以上的计算结论都是在某一方向的网格边界位于“足够远处”得到的,现在把以上得出的最佳网格边界距离综合在一起进行计算比较。
对于模型2D-1:计算TE模式时,左右网格边界和下网格边界都放在3δ处;计算TM模式时,则将左右网格边界和下网格边界放在2δ处。对于模型2D-2,把网格边界全部设置在1δ处即可。综合网格边界条件下部分观测结果如表6所示。
由表6可见,以上利用综合网格边界计算的结果相对误差基本在0.1%以下,说明该网格边界条件下计算结果的可靠性。
3.2 综合模型计算
为了进一步验证综合的最佳网格边界计算结果的可靠性,建立1个较复杂的二维模型,并采用新的频率进行计算。模型2D-3(图4)是在背景介质中赋存3种异常体的较复杂模型,分别在O、O1、O2和B点观测,计算的频率为0.01、0.10、1.00、10.00、100.00、1 000.00Hz,剖分情况与前面相同。
在模型2D-3中存在多个异常体,在确定网格边界变化量度时,需要几个边界变化量度进行比较才能确定。在TE模式计算时,对于低阻体ρ2和ρ4,当它们赋存在较高电阻率的背景介质中时,趋肤深度计算采用背景电阻率,边界变化量度为3δ=503;而当背景介质中存在高阻体ρ3时,趋肤深度计算采用高阻体电阻率ρ3,其边界变化量度为δ =503-。为了确保计算结果正确和保证精度,网格边界变化量度应为TM模式计算时网格边界变化量度的确定与之类似。表7为模型2D-3的部分计算结果。
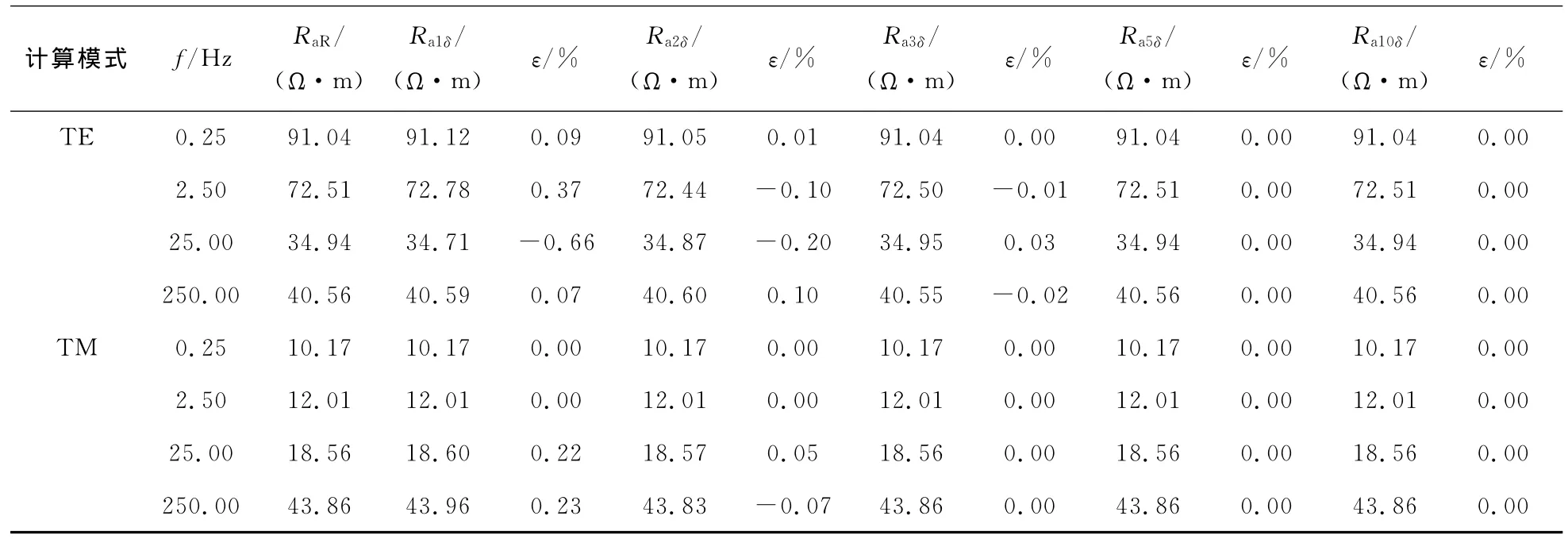
表5 模型2D-1下网格边界变化下O点视电阻率观测结果Table5 Apparent resistivity results of model 2D-1on point Owhen changing bottom boundary
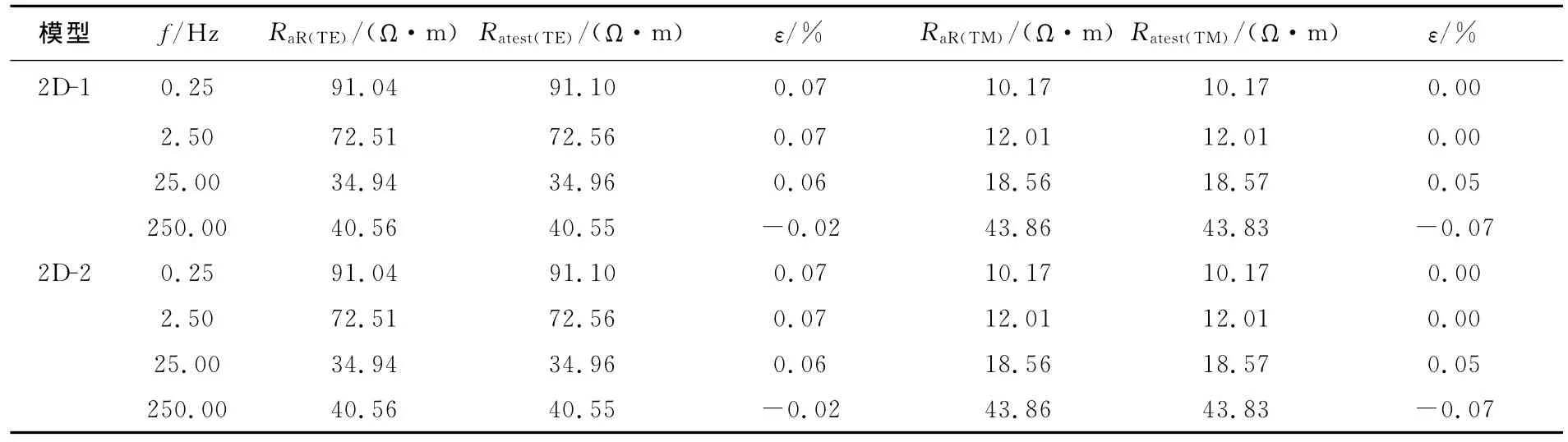
表6 综合网格边界O点观测结果Table6 Observed results on point Owith compositive boundaries
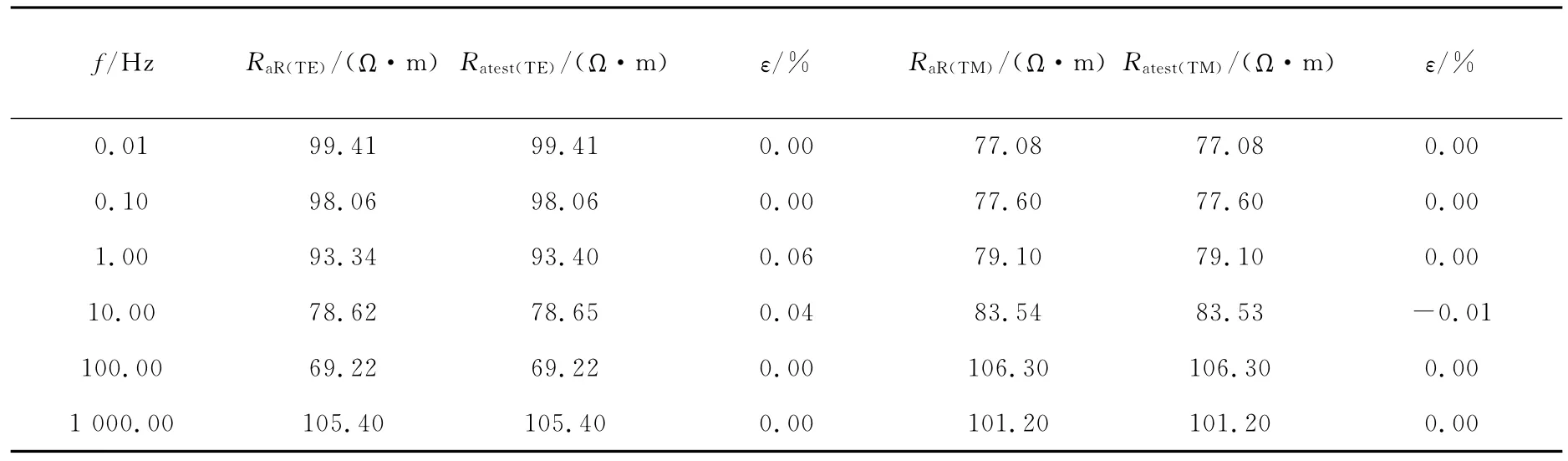
表7 模型2D-3在O点的观测结果Table7 Observed results of model 2D-3on point O
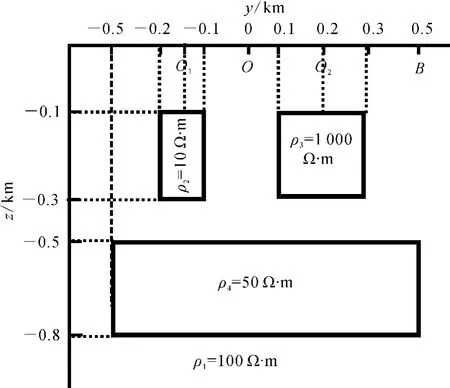
图4 模型2D-3Fig.4 Model 2D-3
由表7可见,利用综合的网格边界计算的结果与参考解的相对误差全部在0.1%以下,进一步验证了综合边界的正确性。
值得注意的是,以上的结果是在背景电阻率和异常体电阻率最大相差一个数量级的情况下得出的。作者又利用综合边界计算了背景电阻率为100 Ω·m、异常体电阻率分别为1、0.1、0.01、0.001 Ω·m的情况以及背景电阻率为100Ω·m、异常体电阻率为200Ω·m的情况,计算结果表明TE模式中误差最大为0.40%,TM模式误差基本为0。另外作者还计算了一些极端的情况,如背景电阻率为1Ω·m、异常体电阻率为2Ω·m的模型和背景电阻率为2Ω·m、异常体电阻率为1Ω·m的模型,发现参考边界在此也适用。
4 结论与建议
利用有限元方法对大地电磁进行模拟计算时,由于存在截断边界影响,从而影响计算结果和精度,或占用大量内存花费较长的时间。笔者通过大量的数值模拟计算与对比,以趋肤深度作为网格边界变化量度,考虑到大地电磁的精度要求,总结得出适合二维大地电磁有限元正演模拟计算的参考网格边界:
1)利用有限元对一维地电模型进行模拟计算时,不存在截断边界的影响,边界条件自然满足。
2)对二维低阻模型进行模拟计算时,以背景电阻率计算趋肤深度作为网格边界变化量度。对于TE模式,当左右网格边界和下网格边界都放在3δ处时,截断边界的影响已可忽略。对于TM模式,左右网格边界和下网格边界在2δ处,截断边界影响可以忽略。
3)对二维高阻模型进行模拟计算时,以高阻体电阻率计算趋肤深度作为网格边界变化量度。不管TE模式还是TM模式,当左右网格边界和下网格边界位于1δ时,截断边界影响已可忽略。
4)当二维地电模型中,同时存在低阻异常体和高阻异常体时,分别以背景介质电阻率和高阻体中电阻率最高者计算趋肤深度,然后根据参考网格边界选择最佳的网格边界。
(References):
[1]Coggon J H.Electromagnetic and Electrical Modeling by Finite Element Method[J].Geophysics,1971,36(1):132-155.
[2]Rodi W L.A Technique for Improving the Accuracy of Finite Element Solution for Magnetotelluric Data[J].Geophysics,1976,44(2):483-506.
[3]Wannamaker P E,Stodt J A,Rijo W L.Two-Dimensional Topographic Responses in Magnetotelluric Modeling Using Finite Element[J].Geophysics,1986,51(11):2131-2144.
[4]Wannamaker P E,Stodt J A,Rijo W L.A Stable Finite Element Solution for Two-Dimensional Magnetotelluric Modelling[J].Geophysics,1987,88(1):277-296.
[5]陈乐寿.有限元法在大地电磁场正演计算中的应用与改进[J].石油物探,1981,20(3):84-103.Chen Leshou.The Improvement and Application of Finite Element Method to 2DForward Solution of Magnetotelluric Sounding[J].Geophysical Prospecting for Petroleum,1981,20(3):84-103.
[6]胡建德,蔡刚.用三角形二次插值有限元法计算二维大地电磁测深曲线[J].石油地球物理勘探,1984,19(4):358-367.Hu Jiande,Cai Gang.Calculating 2DMagnetotelluric Sounding Curve with the Twice Interpolation Triangle Finite Element Method [J]. Oil Geophysical Prospecting,1984,19(4):358-367.
[7]史明娟,徐世浙,刘斌.大地电磁二次函数插值的有限元法正演模拟[J].地球物理学报,1997,40(3):421-430.Shi Mingjuan,Xu Shizhe,Liu Bin.Finite Element Method Using Quadratic Element in MT Forward Modeling[J].Acta Geophysica Sinica,1997,40(3):421-430.
[8]杨长福.大地电磁二维对称各向异性介质的有限元数值模拟[J].西北地震学报,1997,19(2):27-33.Yang Changfu.MT Numerical Simulation of Symmetrically 2DAnisotropic Media Based on the Finite Element Method [J]. Northwestern Seismological Journal,1997,19(2):27-33.
[9]陈小斌.有限元直接迭代算法[J].物探化探计算技术,1999,21(2):165-171.Chen Xiaobin.Direct Iterative Algorithm of Finite Element[J].Computing Techniques for Geophysical and Geochemical Exploration,1999,21(2):165-171.
[10]陈乐寿,刘任,王天生.大地电磁测深资料处理与解释[M].北京:石油工业出版社,1989:1-160.Chen Leshou, Liu Ren, Wang Tiansheng.Magnetotelluric Sounding Data Processing and Interpretation[M].Beijing:Petroleum Industry Press,1989:1-160.
[11]徐世浙.地球物理中的有限单元法[M].北京:科学出版社,1994:220-241.Xu Shizhe.The Finite Element in Geophysics[M].Beijing:Science Press,1994:220-241.
[12]赵广茂,李桐林,王大勇,等.基于二次场二维起伏地形MT有限元数值模拟[J].吉林大学学报:地球科学版,2008,38(6):1055-1059.Zhao Guangmao,Li Tonglin,Wang Dayong,et al.Secondary Field-Based Two-Dimensional Topographic Numerical Simulation in Magnetoteilurics by Finite Element Method[J].Journal of Jilin University:Earth Science Edition,2008,38(6):1055-1059.
[13]刘长生,汤井田,任政勇,等.基于非结构化网格的三维大地电磁自适应矢量有限元模拟[J].中南大学学报:自然科学版,2010,41(5):1855-1859.Liu Changsheng,Tang Jingtian,Ren Zhengyong,et al.Three-Dimension Magnetotellurics Modeling by Adaptive Edge Finite-Element Using Unstructured Meshes[J].Journal of Central South University:Science and Technology,2010,41(5):1855-1859.
[14]Sharma P S,Kaikkonen P.An Automated Finite Element Mesh Generation and Element Coding in 2-D Electromagnetic Inversion[J].Geophysics,1998,34(3):93-114.

