基于人工鱼群算法处理圆度误差

李 媛

(渤海大学 新能源学院，辽宁 锦州 121013)

0 引言

现代化生产对互换性要求越来越高。工业生产中回转体零件是应用最广泛的一种，而圆度误差是机械零件及其互换性的重要指标，往往是产品质量的关键，它在评定机械零件产品质量中起到重要作用。对圆度误差测量的数据处理方法的选定，直接影响圆度误差的计算精度。在圆度误差的评价中，最常用的计算方法为最小二乘法。由于残差为圆心坐标及圆半径的非线性函数，因此不易直接求解，必须运用某种优化迭代算法如遗传算法、单纯形法、Gauss-Newton法、Levenberg-Marquar法等来求解。

人工鱼群算法(Artificial Fish-Swarm Algorithm，AFSA)是由李晓磊等人在2002年提出的一种新型的寻优算法，AFSA算法是集群智能思想的一个具体应用，它的主要特点是不需要了解问题的特殊信息，只需要对问题进行优劣的比较，通过各人工鱼个体的局部寻优行为，最终在群体中使全局最优值突出。本文提供了一种利用AFSA算法处理圆度误差的方法，下面就介绍这种方法的基本原理。

1 人工鱼群算法(Artificial Fish-Swarm Algorithm, AFSA)

人工鱼群算法(AFSA)是一种基于模拟鱼群行为的优化算法。在一片水域中，鱼生存的数目最多的地方就是本水域中富含营养物质最多的地方，依据这一特点来模仿鱼群的觅食、聚群等行为，从而实现全局寻优，这就是鱼群算法的基本思想。

人工鱼个体的状态可表示为向量X=(x1,x2…,xn)，其中xi(i=1，2…，n)为欲寻优的变量；人工鱼当前所在位置的食物浓度表示为Y=f(x)，其中Y为目标函数值；人工鱼个体之间的距离表示为di，j=‖Xi-Xj‖；Visual表示人工鱼的感知范围；Step表示人工鱼移动的步长；δ表示拥挤度因子；try_number表示觅食行为中的重复尝试次数。AFSA初始化一群人工鱼(随机解)，通过迭代搜寻最优解，在每次迭代过程中，人工鱼通过觅食、聚群及追尾等行为来更新自己从而实现寻优。人工鱼的行为描述如下：

1.1 觅食行为

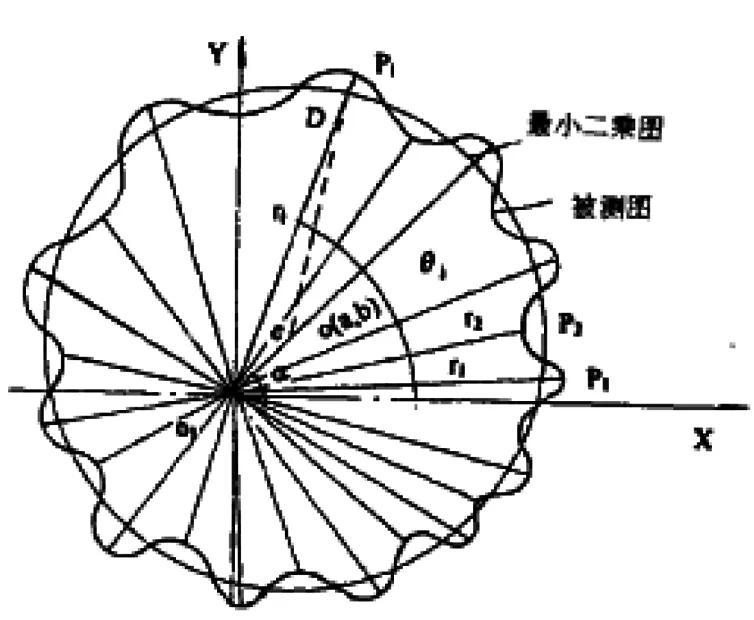
设人工鱼当前状态为Xi，在其感知范围内随机选择一个状态Xj，如果在求极小问题中Yi>Yj，(或在求极大问题中，Yi

1.2 聚群行为

设人工鱼当前状态为Xi，探索当前邻域内(即di，jδYi，表明伙伴中心有较多的食物且不太拥挤，则朝伙伴的中心位置方向前进一步；否则执行觅食行为。

1.3 追尾行为

设人工鱼当前状态为Xi，探索当前邻域内(即di，jδYi，表明伙伴Xj的状态具有较高的食物浓度并且其周围不太拥挤，则朝伙伴Xj的方向前进一步；否则执行觅食行为。

1.4 随机行为

随机行为的实现较简单，就是在视野中选择一个状态，然后向该方向移动，其实它是觅食行为的一个缺省行为。

1.5 公告板

算法中设立公告板，用以记录最优人工鱼个体状态及该人工鱼位置的食物浓度值。每条人工鱼在每一次寻优后，将自身当前状态与公告板进行比较，如果优于公告板则用自身状态取代公告板状态。这样就使公告板记录下历史最优的状态。

2 基于人工鱼群算法的圆度误差评价

以测量中心为圆心，将被测圆划分n等份，且使n为偶数，由此得到n个测量半径r1，r2，…rn。通过测量中心XOY建立直角坐标系，若令通过最小二乘法确定的圆心为O，半径为R，圆心O的直角坐标值为(a，b)，且O1O=e(e为偏心距)(如图1所示)。

由于e远远小于R，并且sin2(θi-α)<1，所以有：εi=ri-R-ecosαcosθi-esinαsinθi

若令a=ecosα，b=esinα，那么就有：[1]

εi=ri-R-acosθi-bsinθi

(1)

图1 最小二乘圆图

在这里我们是利用人工鱼群算法(AFSA)来求半径和圆心直角坐标，这是一个多元线性回归问题。其中ri是圆度测量数据；和是各个等分角度的正弦值和余弦值。有了这些数据之后我们就可以通过上面介绍的人工鱼群算法来对测量数据进行处理。利用人工鱼群算法(AFSA)优化公式(1)中的三个参数半径和圆心直角坐标，可以分以下几个步骤：① 设定参数值：鱼群规模50、最大迭代次数=100、拥挤度因子0.618、人工鱼感知范围= 2.5、移动步长=0.3。②随机生成m条人工鱼个体，作为初始鱼群；③计算目标函数值，找出最小值及其对应的人工鱼个体，并赋值给公告板。③对于每条人工鱼执行以下操作：a) 采用行为选择策略，在追尾行为、聚群行为中选择进步最大的行为作为当前人工鱼的执行行为，找出两者评价行为后的最小值，在执行上述两种行为的过程中的缺省行为是觅食行为。b) 将两种行为执行后的最小值与公告板中的值进行比较，使得公告板中始终保持最小值；并及时更新其对应的人工鱼个体。④如果满足结束条件，转⑤；否则增加迭代次数，转③。⑤程序结束。公告板中的值即为要求的最优值，其对应的人工鱼即为最优的参数。运行程序后得出拟合圆的半径为1.9498mm，拟合圆的圆心c点的坐标为(+2.7734mm,+0.5672mm)，这样通过人工鱼群算法就可以得到圆度误差为0.4681mm。利用同样测量数据根据最小二乘法可以得出拟合圆的半径为1.9495mm，拟合圆的圆心点的坐标为(+2.7738mm,+0.5669mm)，利用最小二乘法得到的圆度误差是0.4682mm。本文提到的方法处理结果和最小二乘法处理结果接近，说明此种方法可行。

3 结语

本文采用人工鱼群算法(AFSA)计算圆度误差，是对传统圆度误差评定方法的一个改进。通过人工鱼群算法(AFSA)计算圆度误差，其精确度非常高，可达到任意给定的精度值，完全满足最小区域法的评定标准，理论上可以无限逼近真实值，从而消除了计算误差。同时，这种算法简单明了，收敛速度快，易于计算机程序实现，该方法为圆度误差评定方法提供了一个新的思路。仿真实验结果表明该方法能够满足圆度误差的评定要求。

[参考文献]

[1] 王树逵，高静. 圆度误差的测量及数据处理[J].阜新矿业学院学报:自然科学版, 1997, 16(6)：733-735.

[2] 田社平. 基于遗传算法的圆度误差评价[J].计量技术，2004(4)：3-5.

[3] 李晓磊，邵之江，钱积新. 一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践，2002，22(11)：32-38.

[4] 李晓磊. 一种新型的智能优化算法-人工鱼群算法[D]. 杭州：浙江大学硕士学位论文，2003.

[5] 高尚，杨静宇. 群智能算法及其应用[M].北京:中国水利水电出版社，2006.

[6] 王辉，钱锋. 群体智能优化算法[J].化工自动化及仪表,2007，34(5)：7-13.

[7] 陈广洲，汪家权，李传军，等. 一种改进的人工鱼群算法及其应用[J].系统工程，2009(12)：105-109.