船舶柴油机的模糊PID调速系统仿真
吴赛赛,朱海峰,陈立伟
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
0 引言
PID控制具有使用方便、适应性强、稳定性强等特点,在过程控制的发展中,PID控制是历史最悠久,生命力最强的控制方式,应用广泛。但传统的PID控制算法在整个控制过程中参数保持不变,这在控制非线性、时变和参数不确定的模型过程时,效果不是太好。而船舶柴油机在不同工况、不同工作环境下,其模型参数都会有较大的变化,传统的PID控制方法很难保证所设定的调速器参数在整个工作过程中保持最优。
模糊控制不要求被控对象的精确模型,对被控对象的非线性、时变性和滞后具有一定的适应能力,鲁棒性较好。把模糊控制与传统PID控制结合为模糊PID,可以对PID控制的参数随着工作条件变化进行整定,减小超调量和调整时间,较好的提高系统的动态、稳态性能,取得良好的控制效果。
1 柴油机模型
柴油机的模型由柴油机本体和执行器两部分组成[1-2]。这里对6135型柴油机进行建模,它的额定转速为1500r/min,功率为75kW。
由动力学原理得柴油机转动平衡方程:
(1)
式中,N为柴油机转速,Ti为指示扭矩,Tf为摩擦损失的扭矩,Tf为负载转矩,Jc为柴油机当量转动惯量。
指示扭矩Ti为:
(2)
式中,qmf为单位时间内喷入气缸的燃油量,HL为燃油低热值,ηi为指示热效率。
指示热效率是转速和空燃比的函数,一般忽略转速的影响,认为它只随空燃比变化,由发动机实验数据采用最小二乘法可拟合出它随空燃比kaf变化的曲线:
ηi=f(kaf)
(3)
空燃比kaf为空气质量流量qma和燃油质量流量qmf之比:
(4)
空气质量流量qma为:
(5)
式中,ηv为充气效率,P为进入气缸的空气气压,V为柴油机气缸总排量,T为气体温度。ηv可认为仅为转速N的函数,可由实验数据进行曲线拟合得到。
摩擦损失的扭矩为:
(6)
式中Cm为活塞平均速度。
电磁执行器可用一阶惯性环节表示,其传递函数可表示为:
(7)
把6135型柴油机的相关数据代入以上式子,在MATLAB/Simulink环境下搭建系统并封装起来,如图1所示[3]。
图1 柴油机封装后模型
2 模糊PID控制器的设计
传统的PID控制的传递函数为:
(8)
式中,Kp为比例系数,Ki为积分系数,Kd为微分系数。三者均为常数。
模糊PID控制根据速度偏差e及偏差变化率ec的大小进行模糊推理得到PID参数Kp,Ki,Kd的修正量dKp,dKi和dKd,使得PID满足不同的误差e和误差变化率ec对控制器参数的不同要求。调速系统结构如图2所示。

图2 模糊PID控制调速系统结构图
2.1 输入输出的模糊化
输入、输出量的论域取为[-6,6],模糊集为{NB,NM,NS,Z0,PS,PM,PB}。为了让所有的e和ec都在论域范围内,输入端乘上模糊化因子ae′,aec,相应的输出端乘上模糊清晰化因子ap,ai,ad。变量隶属函数有高斯形、三角形、梯形等,选取不同的隶属函数会得到不一样的模糊输出[4]。这里输入输出变量隶属函数均选择高斯形。高斯形隶属函数如图3所示。
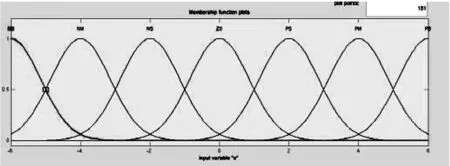
图3 高斯形隶属函数
在模糊逻辑编辑器FIS editor中选择模糊清晰化方法(Defuzzification),可供选择的有最大隶属度法、加权平均法、中位线法等,这里选为最大隶属度法。
2.2 模糊规则的确定
PID控制器中各个参数对控制效果的影响如下[5]:
1) 比例参数Kp的作用是加快系统的响应速度,提高系统的调节精度。随着Kp的增大系统的响应速度越快,系统的调节精度越高,但是系统易产生超调,系统的稳定性变差,甚至会导致系统不稳定。Kp取值过小,调节精度降低,响应速度变慢,调节时间加长,使系统的动静态性能变坏。
2) 积分作用参数Ki的一个重要作用是消除系统的稳态误差。Ki越小系统的稳态误差消除的越快,Ki也不能过小,否则在响应过程的初期会产生积分饱和现象。若Ki过大,系统的稳态误差将难以消除,影响系统的调节精度。另外在控制系统的前向通道中只要有积分环节总能做到稳态无静差。从相位的角度来看一个积分环节就有90度的相位延迟,也许会破坏系统的稳定性。
3) 微分作用参数Kd的作用是改善系统的动态性能,其主要作用是在响应过程中抑制偏差向任何方向的变化,对偏差变化进行提前预报。但Kd不能过大,否则会使响应过程提前制动,延长调节时间,并且会降低系统的抗干扰性能。
根据参数Kp,Ki,Kd对系统输出特性的影响规律,得出模糊控制器对参数Kp,Ki,Kd进行整定的规则:
1) 当e较大时,为了加快系统的响应速度,应取较大的Kp和较小的Kd。另外为了避免系统响应出现较大的超调,此时应去掉积分作用,取Ki=0;
2) 当e和ec为中等大小时,为了使系统响应的超调量减小和保证一定的响应速度,Kp应取小一些。在这种情况下的Kd取值对系统影响很大,应取小一些,Ki的取值要适当;
3) 当e较小时,应取较大的Kp和Ki,使系统具有较好的稳态性能,Kd取值要适当,以避免在平衡点出现震荡。
根据以上分析得到PID参数的修正量dKp,dKi,和dKd的模糊规则[6-7]。表1为dKp、dKi和dKd的模糊规则表。

表1 dKp,dKi和dKd模糊规则表
通过模糊规则表可以得到以下49条控制规则:
1) If(e is NB)and(ec is NB)then(dKpis PB)(dKiis NB)(dKdis PS)
2) If(e is NM)and(ec is NB)then(dKpis PB)(dKiis NB)(dKdis PS)
3) If(e is NS)and(ec is NB)then(dKpis PM)(dKiis NM)(dKdis Z0)
……
4) If(e is PB)and(ec is PB)then(dKpis NB)(dKiis PB)(dKdis PB)
把通过模糊推理的得到的dKp,dKi和dKd分别代入下式计算:
Kx=K0x+dKx×αx
(9)
则得到整定后的PID参数Kp,Ki,Kd。其中K0x,αx表示相应参数的初值和模糊清晰化因子。
打开Rule Editor,把上述的49条控制规则输入,再加上已经建立好的隶属函数,这样就建立好了一个FIS文件,这个FIS文件在仿真时需要调用。在Rule Editor 中依次选择view,rule,分别拖动e和ec下的竖线,可以观察对应不同的e和ec值模糊控制器进行整定的结果dKp,dKi和dKd值(见图4),该值和PID控制器的初始值结合就得到实际运行时PID的参数值。

图4输入输出对应关系图
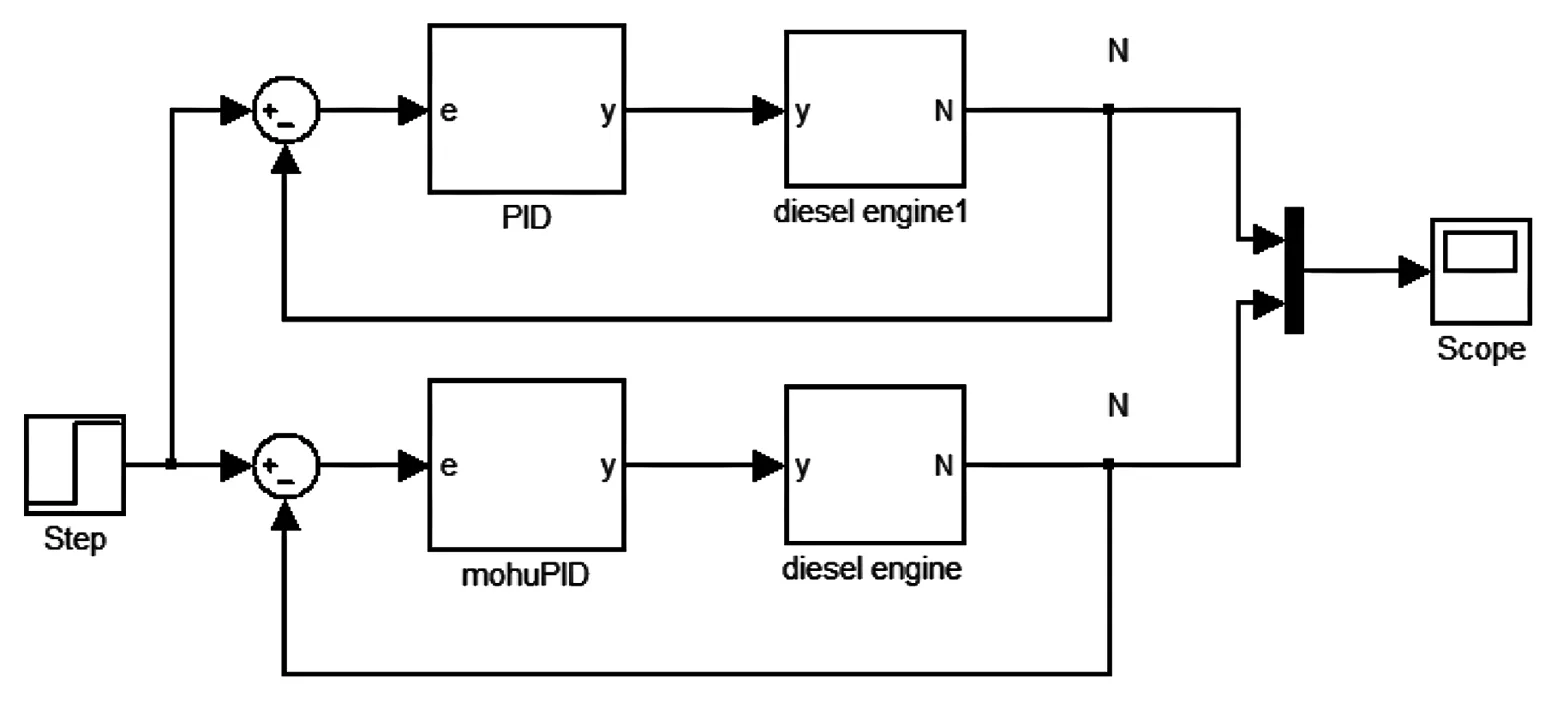
图5模糊PID和PID控制对比模型
3 模糊PID自整定模型的建立和仿真
由以上分析建立6135型柴油机的模糊PID控制和传统PID控制效果对比模型如图5示。其中模块“mohuPID”为封装结构,其内部结构搭建如图6所示。
在MATLAB/Simulink环境下进行仿真:0s时刻,给系统一个单位阶跃信号,在7s时刻给系统施加一外部干扰。仿真数据传递到工作空间,利用绘图函数得到模糊PID控制的输出和传统PID的输出对比如图7所示。
从图7中可以看出模糊PID控制系统比传统PID控制系统上升时间短,超调量小;在出现扰动时,模糊PID控制下系统速度波动小,恢复时间短,调速性能得到提高。
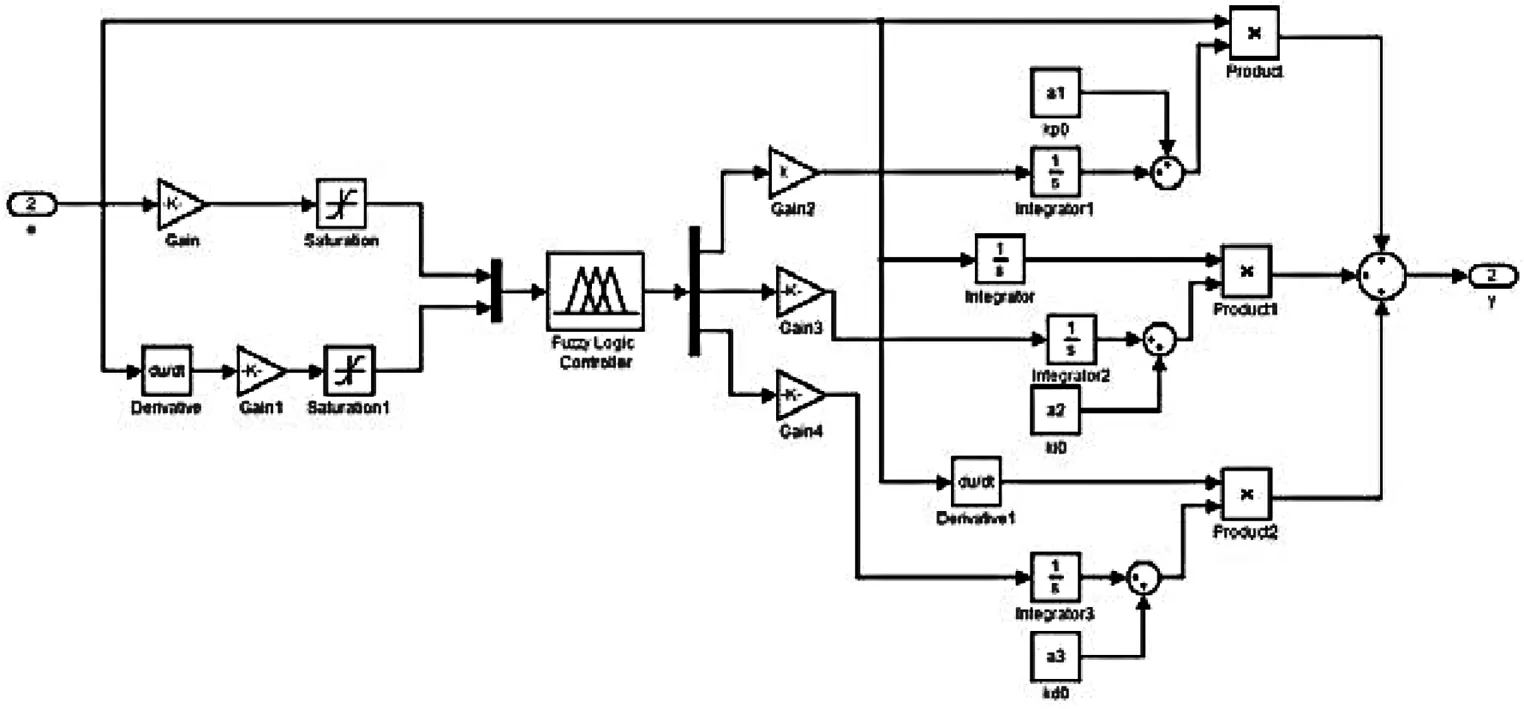
图6模块“mohuPID”内部结构
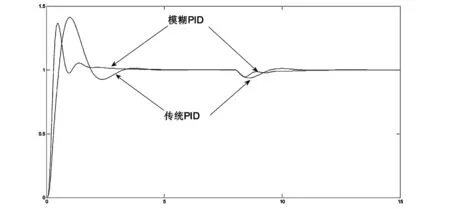
图7模糊PID和传统PID控制结果对比
4 结语
仿真结果表明,对具有非线性、参数时变特性的船舶柴油机转速进行控制时,模糊PID控制与传统的PID控制相比响应时间短、超调量小,在出现扰动时的波动小、恢复时间短,动、静稳定性得到极大提高,能有效的改善柴油机的调速性能。
[参考文献]
[1] 孙立晶.基于模糊-PID算法的柴油机调速控制策略设计与研究[D].哈尔滨:哈尔滨工程大学硕士学位论文,2010.
[2] 徐进.自适应PID在柴油机电子调速中的应用研究[D].哈尔滨:哈尔滨工程大学硕士学位论文,2009.
[3] 陈杰.MATLAB宝典[M].北京:电子工业出版社,2011:711-719.
[4] 王正林,郭阳宽.过程控制与Simulink应用[M].北京:电子工业出版社,2006:52-59.
[5] 石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,北京交通大学出版社,2008:182-189.
[6] 黄文超,张维竞.模糊PID控制的柴油机调速系统仿真[J].计算机应用与软件,2011,28(2):148-151.
[7] 丁连生,丁洪洋.柴油机电子调速系统设计及其Matlab仿真[J].航海工程,2005(1):38-41.

