油田累积产油量的基函数神经网络模型及其预测

王艳芹,王勇 ,刘宇 ,李瑞英

(1.大庆师范学院 物理与电气信息工程学院，黑龙江 大庆163712;2.大庆油田有限责任公司 海拉尔石油勘探开发指挥部开发技术中心，内蒙古 呼伦贝尔 021000)

0 引言

砂岩油田水驱可采储量的预测研究关键在于分析研究累积产油量的变化历程及分布规律。由描述系统状态变化的动态方程分析单层与多层累积产油量的分布特征及其统计规律性，发现其呈S形分布，反映水驱开采多层非均质砂岩油田累积产油量的变化规律性，建立水驱可采储量预测模型，实现油田累积产油量预测。

1 累积产油量分布特征的机理分析

宏观上，在油田开发初期阶段，陆续投产投注，累积产油量呈缓慢递增趋势[1]，S形曲线斜率相对平缓；油田全面注水开发后，油井受效，累积产油量迅速增长[2]，S形曲线的斜率比较大；油田进入高含水后期，多井、层高含水，增产措施效果明显变差，瞬时产油量呈递减趋势[3]，累积产油量S形曲线的斜率又相对变小。根据按S形曲线中拐点出现的早晚可判断油田全面投入开发、全面受效时间的早晚以及受效后采取各种措施使之瞬时产油量达到最大值时间出现的早晚。从油、水相对渗透率曲线出发，可对油田累积产油量的S形分布给予微观上的机理解释。水驱油的全过程实质是流体的渗滤阻力不断降低的过程，初期渗滤阻力大，累积产油量增长缓慢。随着开采时间增长，当油相与水相的渗透率相交即两者相等时，累积产油量的增长幅度达到最高峰。水相渗透率高于油相渗透率后，累积产油量递增幅度越来越小，最终曲线趋于一个极限值。

2 累积产油量的基函数网络模型

由机理分析可见油田水驱累积产油量的分布有较强的相似性，即呈现S形或被拉长的S形分布，并且最终产油量曲线趋于一个确定的极限。基于上述机理分析，可以构造累积产油量的函数型连接神经网络模型，与多层前向网类似，它是一种三层前向网络[4]。输入层由信号源结点组成，第二层为隐含层，隐层单元个数由实际问题需要而定。第三层为输出层，它对输入模式的作用做出响应。从输入层空间到隐含层空间的变换是非线性的，而从隐含层空间到输出层空间的变换是线性的。隐含单元的作用函数的选取是函数型连接网络设计的关键。在理论上隐含单元作用函数的类型的选取尚无一般准则。此处采用的方法是结合系统的实际，通过对系统的机理分析来选取该作用函数的类型。前面已指出，通过机理分析确认，累积产油量分布基本呈S形，可以按S形状的差异选择具有不同形状的S形函数作为隐含层神经元的作用函数。当此作用函数选定后，输入模式到隐含层空间的映射关系就确定了。而隐含层空间到输出空间的映射是线性的，即网络输出是隐含层单元输出的线性加权和，而函数型连接神经网络正是靠多个非线性神经元的“集体”计算能力的总和去最佳逼近一个复杂非线性系统的未知模型。并且这类神经网络较通常的神经网络有更快的收敛速度。

设y(t)表示某油田某区块第t年的累积产量。我们选用几种具有不同S形非线性函数来设计函数型连接网络(FLN)。

2.1 指数函数型连接神经网络

在单输入单输出的情况下，指数函数型连接网络确定的输入输出关系如下：

(1)

其中wi是第i个隐含单元输出的连接权值，f(ai,t)=1-e-ait是第i个隐含单元的作用函数。显然它有明显的S形状，符合油田水驱累积产油量的分布规律。

2.2 Logistic函数型连接神经网络

Logistic函数有如下形式：

y(t)=1/[Q-1+(y(t0)-1-Q-1)exp(-b(t-to))]

(2)

其中Q为水驱可采储量，它是累积采油量的极限值，b>0为扩散系数。t0为油田某区块初始生产时间。Logistic模型具有较对称S形状，常用于油田累积产量预测。然而仅用一种函数拟合一个非线性系统，总会存在一定误差，而用FLN，即用多个非线性神经元的“集体”计算与拟合，才能以任意要求的精度逼近实际系统。为此构造Logistic函数连接神经网络，其输入输出关系为：

(3)

其中，f(bi,θi,t)是第i个 Logistic型神经元变换函数，wi为隐含层第i个神经元的权值。

2.3 Gompertz函数型连接神经网络

油田预测中常用的Gompertz模型如下：

y(t)=Qexp[ln(y(t0)/Q·exp(-b(t-t0)/ln(Q)]

(4)

其中b和Q分别为扩散系数和可采储量。若以n个形如上式的Gompertz函数作为神经网络的隐含层神经元的作用函数，则可给出Gompertz函数连接神经网络，其输入输出关系为

(5)

在上面三种函数型连接神经网络中，有一个共同特点，即网络的输入输出映射F(w,θ,t)关于权向量w是线性的，关于参数向量θ是非线性的。根据这一特点，采用交互辨识技术：用递推最小二乘法(RLS)估计网络的权向量，用适用于非线性系统参数辨识的学习算法辨识参数向量。例如可采用BP算法，但它的收敛速度慢。为此可采用文献[5]的二阶算法估计参数。当网络模型的权向量w和θ被辨识后，则可依据上述网络模型进行累积产油量预测，设t是当前时间，k>t是预测的时间(k=t+1,t+2,…)，则分别有预测模型：

(6)

(7)

(8)

3 油田累积产油量的建模和预测

对某油田采油厂区块多组累积产油量数据建模和预测。限于篇幅仅给出其中一组。数据前带“*”号的为有验证预报，带“△”的为无验证预报。

对该区块用式(3)的Logistic函数网络模型进行拟合和预报。取实际数据12组，前9组用于网络训练，后3组用于有验证预报。网络结构为1-3-1，用递推最小二乘法估计权向量，用文献[5]的二阶算法辨识参数向量。依据训练好的网络又进行1组预测。其拟合值和预报值见表1。

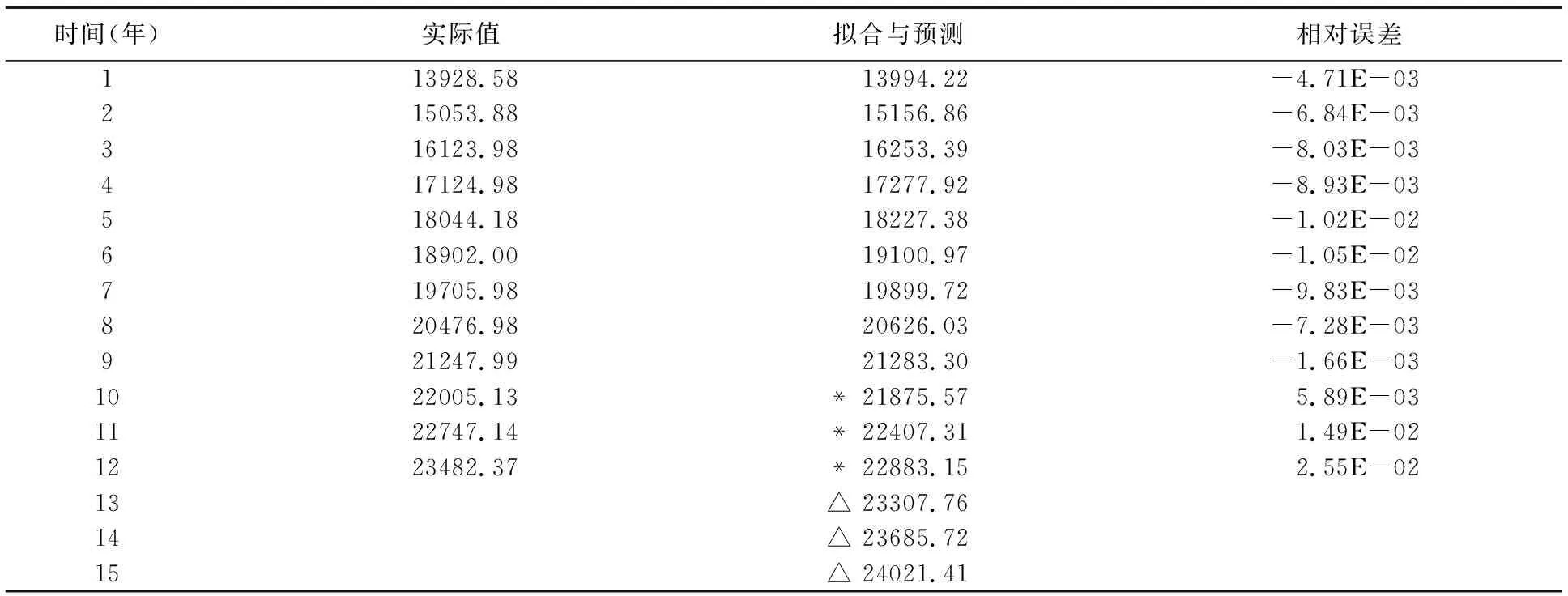
表1 区块3拟合和预测结果

4 结语

通过对油田累积产油量系统的机理分析和趋势性分析，在非线性函数空间中确定了若干组基函数，以这些非线性基函数为神经元模型，建造了函数型连接网络模型。应用指数、Logistic和Gompetz函数型连接网络模型，对某油田采油厂若干区块多组累积产油量数据建模和预测，三个区块有验证预报最大相对误差分别为1.68E-02，4.56E-02和2.55E-02。精度完全能够满足实际需要，表明上述方法的有效性。该方法对油田的开发指标预测，经济评价分析，高效开发油田具有重要意义。

[参考文献]

[1] 罗鹏飞.注水砂岩油藏稳产研究与实践[J].内江科技, 2012(5):152-153.

[2] 高锋博.王家湾中区高含水期注水效果分析[J].石油地质与工程,2012,26(4):71-72.

[3] 邹建栋.注水开发油藏生产递减预测分析[J].辽宁化工, 2012,41(8):867-870.

[4] 徐丽娜.神经网络控制[M].北京:电子工业出版社,2003:26-29.

[5] 王艳芹,王凤嫔.非线性系统的RBF神经网络建模方法研究[J].大庆师范学院学报，2010,30(6):23-25.