混沌系统的单变量微分状态观测器的同步控制

牟 俊, 初 冉, 崔 远 慧

( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )

0 引 言

1990年,美国学者Pecora和Carroll[1]在电子学线路的专门设计的实验中实现了两个系统的混沌同步,立即引起了广泛的关注。混沌行为的最大特点就是运动轨线对初始条件具有高度的敏感性,所以以前人们认为在实验室内要想重构完全相同(同步)的混沌简直是不可能的事情。混沌同步的发现打破了这个禁锢,从而在以保密通信为首的许多领域显示出广阔的应用发展前景,成为研究的热点[2]。到目前为止,关于混沌系统的同步研究已经取得一定成就:孙克辉等实现了混沌系统在噪声干扰下的同步[3]及投影同步[4],刘杰等[5]实现了混沌系统的追踪同步,陆君安等[6]实现了混沌系统的自适应反馈同步。但这些同步方案由于同步时间长、计算量大而离实际应用都还有一定差距。基于状态观测器的同步方案[7]具有易于在工程上实现、不需要计算同步系统的条件Lyapunov指数等优点,因而受到广泛关注。本文通过设计合适的单变量状态观测器,实现了混沌系统的同步。

1 混沌系统同步研究

1.1 单变量微分状态观测器理论分析

混沌系统

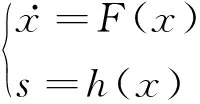
(1)

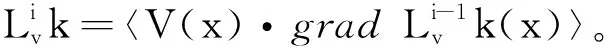
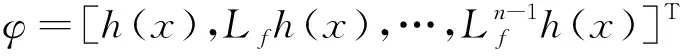
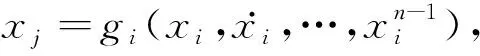
(2)

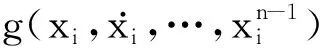
定理2[9]设系统(1)的输出为

(3)

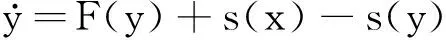
1.2 基于Lorenz混沌系统的状态观测器设计

Lorenz混沌系统的数学模型为

(4)

其系数矩阵为

根据式(2)可得:

当上式成立时,驱动系统的驱动量为

其中

接收端系统可相应表示为

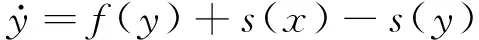
(5)

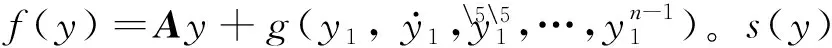
2 混沌系统同步仿真与结果讨论

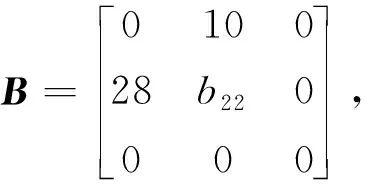
对于Lorenz混沌系统,从系统参数、初值、b22取值等方面,研究同步系统的同步性能。

2.1 各系统变量同步仿真

对于Lorenz系统,取b22=29。系统初始值如上。同步Lorenz系统各参数同步曲线如图1所示。可见,虽然发送端与接收端初值相差很远,但经过一段时间均能完全满足同步要求。证明了上述状态观测器设计方法对于混沌系统有效。

图1 Lorenz系统的同步收敛曲线

Fig.1 Curve of synchronous convergent in Lorenz system

2.2 b22取值对同步性能的影响

Lorenz系统其他参数取值不变,并设e=[(y1-x1)2+(y2-x2)2+(y3-x3)2]1/2。b22=50,b22=20,b22=0三种不同状态系统的同步误差信号如图2所示。此处仿真取每秒系统迭代100次。可见,只要满足基本条件b22>-1,系统最终将实现精确同步,在所有其他条件均相同的情况下,b22越大,系统同步收敛越快。

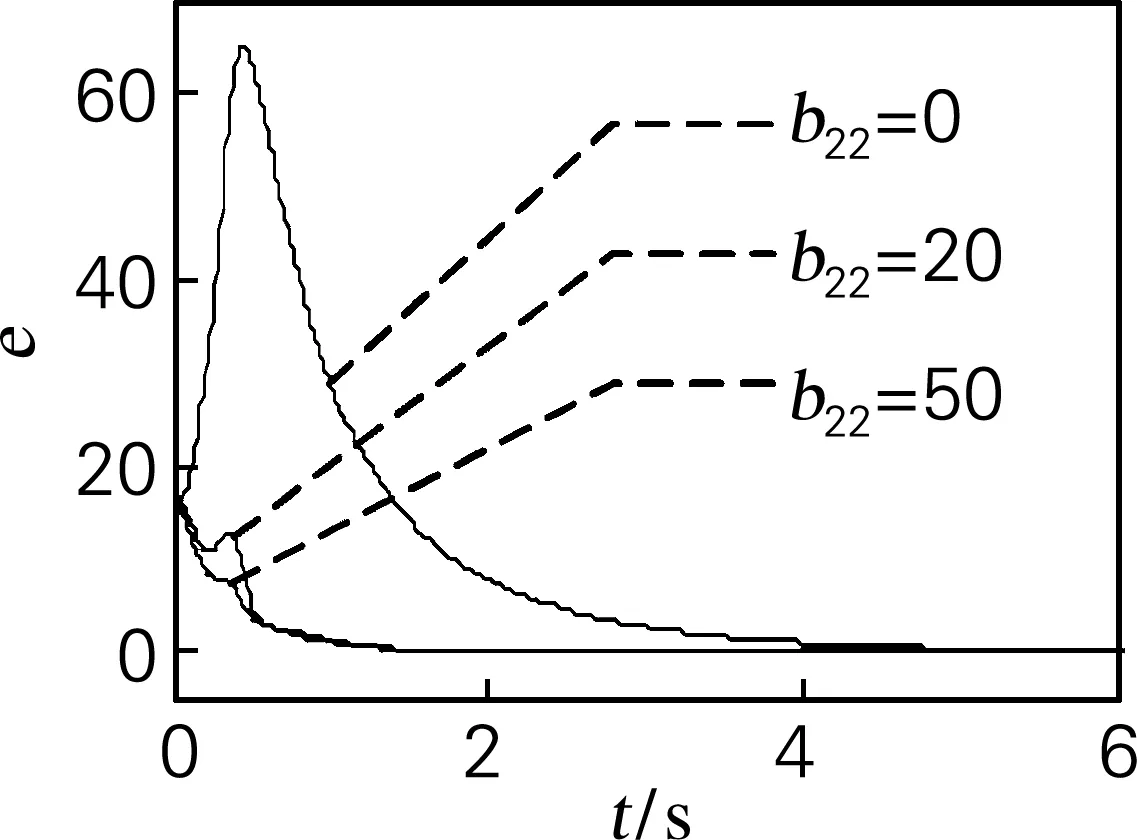
图2 b22不同取值时的同步误差收敛曲线

Fig.2 Curve of synchronous error convergent with differentb22

2.3 系统初值对同步性能的影响

Lorenz系统其他参数取值不变,并取b22=29,同时设e=[(y1-x1)2+(y2-x2)2+(y3-x3)2]1/2,取b22=29,当取系统初值分别为

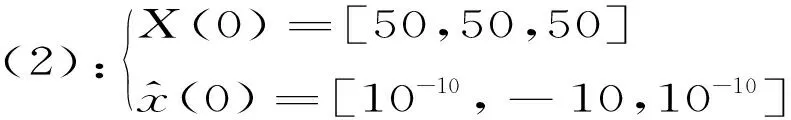
时,系统的同步误差信号如图3所示。

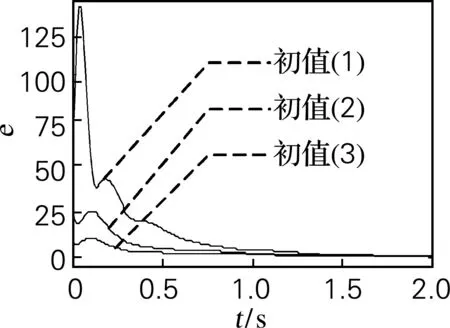
图3 不同初值条件下的同步误差收敛曲线

Fig.3 Curve of synchronous error convergent with different initial value

由图3可见,在其他初始条件一定的情况下,达到同步所需的时间仅与初始条件下发送端的统一混沌系统和接收端的状态观测器之间初值差的大小有关。初值差越大则实现同步所需时间越长。但总体来说,只要系统的初值位于混沌吸引子内部,即使发送端与接收端初值相差很远,也能在一定时间内达到精确同步。

3 结 论

本文采用单变量微分状态观测器方法,设计了混沌系统的状态观测器同步方案,并以Lorenz系统为目标系统,对该同步方案的同步性能进行了分析。该方案实际上是基于状态空间重构技术,由于采用了状态观测法,所以不需计算系统的条件Lyapunov指数,且发送端系统与接收端状态观测器之间可取完全不同的初值。在同步过程中,采用单参数传输,大大提高了信道利用率。就同步性能来讲,该方案同步时间短,同步性能良好。在实际应用中,为使系统同步性能优化,减少同步振荡,缩短同步时间,系统参数的选择比较关键。该方案在保密通信中应用前景广阔。

[1] PECORA L M, CARROLL T L. Synchronization in chaotic system[J]. Physical Review Letters, 1990, 64(8):821-824.

[2] 方锦清. 驾驭混沌与发展高新技术[M]. 北京:原子能出版社, 2001：243-244.

[3] 孙克辉,牟俊. 基于状态观测器方法的统一混沌系统同步研究[J]. 信息与控制, 2006, 35(3):335-338.

[4] 孙克辉,丘水生. 简化Lorenz混沌系统的投影同步控制[J]. 电路与系统学报, 2011, 16(1):7-11.

[5] 刘杰,陈士华. 一类混沌系统的追踪控制与同步[J]. 数学杂志, 2002, 22(3):341-344.

[6] LU Junan, WU Xiaoqun, HAN Xiuping, et al. Adaptive feedback synchronization of a unified chaotic system[J]. Physics Letters A, 2004, 329(4/5):327-333.

[7] 牟俊,王智森,康丽. 统一混沌系统的状态观测器同步控制及其在保密通信中的应用[J]. 大连工业大学学报, 2008, 27(2):162-166.

(MOU Jun, WANG Zhisen, KANG Li. Synchronous control of an unified chaotic system based on stated observer and the application in the secure communications[J]. Journal of Dalian Polytechnic University, 2008, 27(2):162-166.)

[8] MAY R M. Simple mathematical models with very complicated dynamics[J]. Nature, 1976, 261:459-467.

[9] FEIGENBAUM M J. The universal metric properties of nonlinear transformations[J]. Journal of Statistical Physics, 1979, 21(6):669-706.