中国A股市场股票收益率风险因素分析:基于Fama－French三因素模型

刘 辉，黄建山

(1.西安交通大学经济与金融学院，陕西西安，710061;2.上海证券交易所，上海，200120)

中国A股市场股票收益率风险因素分析:基于Fama－French三因素模型

刘 辉1，黄建山2

(1.西安交通大学经济与金融学院，陕西西安，710061;2.上海证券交易所，上海，200120)

本文以中国A股市场上市公司为样本，基于Fama－French三因素模型，实证分析了中国A股市场股票收益率的风险因子。研究结果表明，Fama－French三因素模型较CAPM模型能更好地解释中国A股市场的股票收益率;中国A股市场股票收益率存在规模与价值效应，股票(或股票组合)收益与公司规模呈显著负相关关系，而与公司账面市值比呈显著正相关关系。

A股市场;股票收益率;市场因子;规模因子;价值因子

特别声明:本文仅代表作者观点，与作者供职单位无关。

中国证券市场经过二十多年的发展，市场规模迅速壮大，初步成长为具有全球影响力的资本市场。截至2012年底，中国股市已有2494家上市公司，23.04万亿市值，投资者开户数达到2.11亿户，中国股市成为了中国经济最重要的组成部分。同时，市场体系不断健全，市场功能不断增强，由深沪主板、中小板和创业板等组成的股票市场体系逐步建立和不断完善。国内关于我国资本市场规模效应与价值效应的研究表明，我国资本市场存在着显著的规模效应和价值溢价现象。

其实，资本市场定价问题一直是金融学研究的热点、重点问题，而关于股票市场投资收益的讨论更是学术界和实业界关注的焦点。从理论上讲，投资者在进行投资时需要考虑各种资产的期望收益和风险。现代投资理论的奠基人Markowitz认为，以证券投资收益率的方差作为投资风险的衡量因子，并将投资风险划分为系统风险和非系统风险等两类。Sharp和Lintner在组合投资理论的基础上，发展了资本资产定价模型(CAPM);在CAPM模型中，市场组合包含了可交易的每一支股票，单只股票的风险以其与市场组合收益率共同变动程度即beta值来衡量。CAPM理论因其逻辑的简洁性受到了理论界和实务界的极大关注，很多实证研究结论也支持了CAPM理论。然而，从实践角度来看，CAPM模型过于抽象而忽视了很多实际因素，在一定程度上过多脱离实际而假设，这限制了CAPM模型的实际应用，出现了许多CAPM模型无法解释的新现象，如无法解释股票横截面收益率。新现象被金融学家发现并展开了深入研究，从而产生了新的理论。比如关于资本市场价值溢价和规模效应的研究，在理论界和实业界收到了广泛关注。

基于此，本文研究的目的正是考察我国股票市场的规模效应和价值溢价现象，检验CAPM模型对于国内股票收益率的解释力度。在重点研究规模因素、价值因素对于公司基本面风险的反映能力之后，本文力图验证 Fama－French三因素模型在国内市场的适用性，并对CAPM与 Fama－French三因素模型进行比较分析。

本文结构如下:首先，从理论视角回顾股票收益、价值溢价、规模效应等相关文献;其次，利用国泰君安CSMAR研究数据库1995年1月1日至2011年12月31日的股票行情数据和公司财务数据，以上海和深圳两市的A股股票为样本，通过计算日收益率，对标准形式的CAPM的有效性进行检验;再次，运用Fama－French三因素模型进行检验，并比较分析两种模型对我国股票收益率的解释力度;最后对研究结论分析，并提出针对性政策建议。

一、关于CAPM模型和Fama－French三因素模型的研究述评

关于CAPM模型，有很多国内外学者都进行了研究。其中，Sharpe［1］、Lintner［2］和 Black［3］的研究表明，个股或股票组合的预期收益与其市场风险β(beta)线性相关，而且β是其预期收益的唯一决定因 素。 Black、Jensen 和 Scholes［4］，Blume 和Friend［5］，Fama 和 MacBeth［6］等学者的研究结论都支持了CAPM理论的核心观点，其中，Black、Jensen和 Scholes［4］以纽约证券交易所(NYSE)1931 年至1965年间股票数据为样本进行检验，研究结果表明，低风险的股票获取了理论预期收益，而高风险的股票收益低于理论预测。Fama和 MacBeth［6］以1935年至1968年间美国股票402个月度数据为样本进行分析，检验结果表明，股票收益与beta值呈正相关关系，而其他非系统性风险因子与股票收益不显著相关。

国内外学者越来越多的研究结论不支持CAPM模型。Roll［7］首先对CAPM模型的实证检验提出质疑:由于无法证明市场指数组合是否有效，因而无法对CAPM模型进行检验，并据此提出了套利定价理论(APT)，即假设在竞争性和无摩擦的市场上，股票收益率与未知数量的未知因素相关，并根据这一假设推断认为，CAPM模型仅仅是一种最简单的单因素模型。

针对CAPM模型的检验逐渐由单一beta的检验转向多变量的分析，多变量的研究认为，CAPM模型中的beta并不能完全解释股票资产的横截面预期收益。Banz［8］的研究认为，除了 β以外，市值(ME)(股票价格*总股本)也对股票平均收益率有较好的解释能力，在特定的β条件下，低市值的股票拥有更高的平均收益率，而高市值的股票却拥有较低的收益率，这就是股票收益率的规模效应。其他学者的研究还发现，美国股票平均收益率与账面市值比率正相关，账面市值比越高的公司，平均而言也将获得更高的股票收益率［9－10］;公司财务杠杆也能部分地解释股票收益率差异，负债比率越高的上市公司，其股票平均收益率越大［11］;BE/ME(账面价值/市场价值)在日本股票市场上对股票平均收益率有较高的解释能力［12］;美国股票市盈率对平均收益率具有解释能力［13］。在前人研究的基础上，Fama和French［14］对美国股票收益率的影响因素进行了深入研究，并对CAPM模型之外的、对股票预期收益有影响的其他因子进行系统检验，结果发现，股票市场的β值无法解释横截面上不同股票收益率差异性，而公司总市值、账面市值比等因子可较好地解释横截面上股票收益率的差异性。进一步研究发现，市场资产组合因子(Rm－Rf)、规模因子(SMB)、账面市值比因子(HML)等三个因素可对投资组合(包括单个股票)的超额收益率作出较好解释［15］，解释能力较CAPM模型强。

此后，很多学者的研究进一步证实，Fama－French三因素模型比CAPM单因素模型更能解释股票超额收益率。比如，Chui［16］以亚太地区5大新兴资本市场股票为样本，对股票收益率与β系数、公司规模、账面市值比之间关系进行实证检验，结果表明，股票收益率与β系数的关系在统计上不显著，而与公司规模、账面市值比的关系通过显著性检验，这与Fama－French三因素模型的研究结论基本一致。Drew［17］也以几个主要的亚洲证券市场为样本，对Fama－French三因素模型进行检验，检验结果与Fama－French三因素模型基本符合。

近年来，国内学者也研究了中国股票市场上CAPM的有效性，并对Fama－French三因素模型在中国股票市场的适用性进行研究。比如陈信元［18］以上海市场股票为样本进行研究，发现规模因子(Size)与价值因子(BE/ME)等对股票收益率具有显著相关关系;邓长荣［19］以深市数据为样本进行检验，结论也证明Fama－French三因素模型成立。

在上述研究的基础上，本文运用 Fama－French三因素模型对A股市场的日回报率数据进行实证检验，并与CAPM模型的实证结果进行比较分析，以验证我国A股市场是否支持Fama－French三因素模型，并对具有哪些特征的公司更支持 Fama－French三因素模型进行分析;最后基于研究结论提出政策建议。

二、我国股票市场收益率风险因素:基于Fama－French三因素模型的实证检验

(一)样本来源及检验方法

本文以上海和深圳两市的A股股票为样本，样本区间为1995年1月1日至2011年12月31日，股票行情数据和公司财务数据来自CSMAR数据库和Wind数据库。

本文采用 Black，Jensen ＆ Scholes［4］的时间序列回归方法，用股票(或股票组合)的日回报率对市场因子、规模因子和账面市值比因子进行回归分析。

(二)关于风险因子和投资组合的构造

本文依照Fama与French［15］在三因素模型中构造风险因子的方法，将A股股票按市值ME大小分为两组:将市值小的50%定义为S组，将市值大的50%定义为B组;类似地，将A股股票按账面市值比BE/ME分为三组:账面市值比最高的30%的股票定义为H组，将账面市值比最低的30%的股票定义为L组，中间的40%的股票定义为M组。具体组合构造过程如下:

每年按照A股所有股票的ME从小到大排序，把所有股票分为2组:小公司(small firm)50%和大公司(big firm)50%，其中，ME为t年6月末的A股市场(包括沪市和深市)所有股票的市场价值(包括流通股和非流通股)。

每年按BE/ME从高到低排序后，分成高、中、低3 组:High(30%)、Median(40%)、Low(30%)，其中，BE为(t－1)年会计年度末的A股市场(包括沪市和深市)所有股票的账面价值，ME为(t－1)年12月末的A股市场(包括沪市和深市)所有股票的市场价值(包括流通股和非流通股)。

按照上面的分类方法，构造6个投资组合(S/L，S/M，S/H，B/L，B/M，B/H)，并标记 t年7 月初到(t+1)年6月末的所有A股股票;从t年7月初到(t+1)年6月末，分别计算这6个投资组合的加权日回报率。接着，利用这6个投资组合的加权日回报率计算风险因子:公司规模因子:SMB=(S/L+S/M+S/H)/3 － (B/L+B/M+B/H)/3，公式表示的是剔除BE/ME因素后小规模SIZE与大规模SIZE组合的日收益率差。

账面市值比因子:HML=(S/H+B/H)/2－(S/L+B/L)/2，公式表示的是剔除SIZE因素后高BE/ME与低BE/ME组合的日收益率差。

另外，利用市场数据计算超额市场回报率Rmf=Rm– Rf，其中，Rm代表考虑红利再投资的A股股票的日平均回报率;Rf是3个月期的定期储蓄利率所折算的日利率，代表无风险利率。

三、Fama－French三因素模型检验结果及讨论

Fama－French三因素模型模型假设条件包含理论假设和统计假设等两个部分。理论假设包括存在着大量投资者;所有投资者都在同一证券持有期计划自己的投资资产组合;投资者投资范围仅限于公开金融市场上交易的资产;不存在证券交易费用(佣金和服务费用等)及税赋;投资者们对于证券回报率的均值、方差及协方差具有相同的期望值;所有投资者对证券的评价和经济局势的看法都一致。其次是统计假设，基本假设为:(Rm－Rf)、SMB、HML与随机误差项ξ不相关;零均值假定:E(ξi)=0;同方差假定，即ξ的方差为一常量;无自相关假定:COV=(ξi，ξj)=0，i≠ j解释变量之间不存在线性相关关系，换言之，两个解释变量之间不存在确切的线性关系;假定随机误差项ξ服从均值为0，方差为S2正态分布，即 ξi～ N(0，S2)。

Fama－French三因素模型表示为:

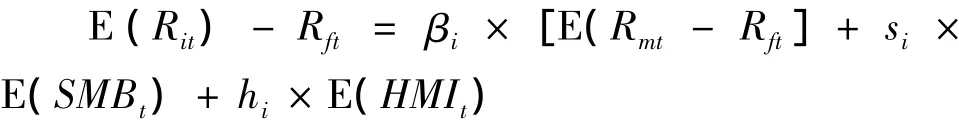
其中，Rft表示时间t的无风险收益率;Rmt表示时间t的市场收益率;Rit表示资产i在时间t的收益率;E(Rmt)－Rft是市场风险溢价，SMBt为时间t的市值(Size)因素的模拟组合收益率，HMIt为时间t的账面市值比(book－to－market)因素的模拟组合收益率。

βi、si和hi分别是三个影响因子的系数，回归模型表示如下:

本文研究中考虑了现金红利再投资后的收益率。对于不考虑现金红利再投资的情况，我们也进行了检验，结果完全一致，故不再列出。

表1 中国沪、深A股2×3投资组合日收益率(CAPM模型)

从表1可以看出，CAPM模型回归的结果R2值比较高，且β系数均显著，大小在1左右变化，且与股票组合的规模和账面市值比没有显著关系。但是，从α值的t值检验来看，有3组投资组合的α值在统计上显著，且均为小公司投资组合。也就是说，CAPM能较好地解释了大公司投资组合的超额收益率，但是却不能完全解释小公司投资组合的超额收益率。但是，从表1中，我们也可以看出来，α值都很小，所以尽管小公司投资组合α值在统计上显著，但对结果影响也不大。

从表2可以看出，Fama－French三因素模型回归的结果的R2值均超过0.9，且均比CAPM模型回归结果的R2值高;β系数也在统计上显著;对新增加的两个因子HML和SMB中，除了因子SMB在bm投资组合略微不显著外，其余均在统计上显著。从截距项α值来看，均在统计上不显著，且基本比CAPM的α值小，这说明Fama－French三因素模型不仅能很好地解释大公司投资组合的超额收益率，而且也能够很好地解释小公司投资组合的超额收益率。

另外，从表2中，我们还可以看出，小公司投资组合的s值远远大于大公司投资组合的s值;同时，h值的回归值随着账面市值比从小到大递增，这也验证了我国A股市场股票(或股票组合)的平均报酬与公司规模呈现负的相关关系，而与公司的账面市值比呈现正的相关关系。

表2 中国沪、深A股2×3投资组合日收益率(Fama－French三因素模型))

四、研究结论与政策建议

本文以我国A股市场股票为样本，基于Fama－French三因素模型进行实证分析了中国A股市场股票收益率的风险因素。研究结果表明，影响股票收益率的三个主要因子(市场因子、规模因子和价值因子)对中国A股市场依然有效。中国A股市场股票收益率存在规模与价值效应，特别是对于规模较小的公司来说，股票(或股票组合)收益与公司规模呈显著负相关关系，而与公司账面市值比呈显著正相关关系。

Fama－French三因素模型尽管充分考虑了公司规模和账面市值比对股票收益率的影响，在一定程度上改善了CAPM模型对中国股票投资组合收益率的解释能力，然而，从本文对1995年1月1日到2011年12月31日中国A股市场日收益率的回归结果可以看出，这种改善并不明显，CAPM模型基本可以解释中国A股市场的超额收益率。

总之，对于CAPM模型而言，其仍能够作为一个有用的投资管理工具，那些认为β已经彻底死亡的报道还为时尚早。对于Fama－French三因素模型而言，本文结论能够用于选择证券组合、评估组合业绩、测量超额回报和估计资本成本等需要估计预期股票回报率的领域，一个备选组合与三个因素(市场因子、规模因子和价值因子)的关系，可以用这个组合过去的超额回报对这三个因素(市场因子、规模因子和价值因子)的回归来估计，回归的斜率及历史平均回报值可用于估计该组合的预期回报，还可以评估组合业绩;一个组合对三个因素(市场因子、规模因子和价值因子)的回归截距为超额平均回报，可用来判断一个管理者能否超越市场平均收益，获取高于市场的超额收益。

［1］Sharpe W F.Capital asset prices:A theory of market equilibrium under conditions of risk ［J］.Journal of Finance，1964，19:425－442.

［2］Lintner J.The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets［J］.Review of Economics and Statistics，1965，47:13－37.

［3］Black F.Capital market equilibrium with restricted borrowing［J］.Journal of Business，1972，45:444 －455.

［4］Black F，Jensen M，Scholes M.The capital asset pricing model:Some empirical tests［A］.Jensen M.Studies in the theory of capital markets［C］.New York:Praeger，1972.

［5］Blume M，Friend I.A new look at the capital asset pricing model［J］.Journal of Finance，1973，28:19 － 33.

［6］Fama E，MacBeth J.Risk，return and equilibrium:Empirical tests［J］.Journal of Political Economy，1973，81:607－636.

［7］Roll R.A critique of the asset pricing theory's test:Part I.On past and potential testability of the theory［J］.Journal of Financial Economics，1977，4:129 －176.

［8］Banz R W.The relationship between return and market value of common stocks［J］.Journal of Financial Economics，1981，9:3－18.

［9］Stattman D.Book values and stock returns［J］.The Chicago MBA:A Journal of Selected Papers，1980，4:25－45.

［10］Rosenberg B，Reid K，Lanstein R.Persuasive evidence of market inefficiency［J］.Journal of Portfolio Management，1985，11:9 －16.

［11］Bhandari L C.Debt/equity ratio and expected common returns:Empirical and evidence［J］.Journal of Finance，1988，43:507 －528.

［12］Chan L K，Hamao C Y，Lakonishok J.Fundamentals and stock returns in Japan［J］.Journal of Finance，1991，46:1739－1789.

［13］Basu S.The relationship between earnings yield，market value，and return for NYSE common stocks:Further evidence［J］.Journal of Financial Economics，1983，12:129－156.

［14］Fama E F，French K R.The cross－section of expected stock returns［J］.Journal of Finance，1992 ，47:427－465.

［15］Fama E F，French K R.Common risk factors in the returns on stocks and bonds［J］.Journal of Financial E－conomics，1993，33:3－56.

［16］Andy C W，Chui K C，Wei J.Book－to－market，firm size，and the turn－of－the－year effect:Evidence from Pacific－Basin emerging markets［J］.Pacific － Basin Finance Journal，1998，6:275 －293.

［17］Drew M E，Veeraraghavan M.Explaining the cross－section of stock returns in the Asian region［J］.International Quarterly Journal of Finance，2001，1:205－ 221.

［18］陈信元，张田余，陈冬华.预期股票收益的横截面多因子分析:来自中国证券市场的经验证据［J］.金融研究，2001(6):22－35.

［19］邓长荣，马永开.三因素模型在中国证券市场的实证研究［J］.管理学报，2005，2(5):591－596.

Risk Factor Analysis of Chinese A Share Market's Stock Return Rate:Based on Fama-French Three Factor Model

LIU Hui1，HUANG Jian－shan2
(1.School of Economics and Finance，Xi'an Jiaotong University，Xi'an 710061，China;2.Shanghai Stock Exchange，Shanghai 200120，China)

This paper takes the listed companies of Chinese A share market as sample and positively analyzes the risk factors of Chinese A share market's stock return rate based on Fama－French three factor model.The research result indicates that Fama－French three factor model can better explain the stock return rate of Chinese A share market than CAPM.The stock return rate of Chinese A share market has scale and value effect.Significant negative correlation exists between stock(or stock combination)return rate and a company's scale and significant positive correlation exists between it and a company's book market capitalization.

A Share Market;Stock Return Rate;Market Factor;Scale Factor;Value Factor

A

1002－2848－2013(04)－0027－05

2013－06－07

刘辉(1971－)，湖南省益阳市人，西安交通大学经济与金融学院博士研究生，研究方向:产业经济学;黄建山(1982－)，广西壮族自治区百色市人，经济学博士，上海证券交易所，研究方向:产业经济学。

责任编辑、校对:郑雅妮