数控机床用多步进电机伺服系统控制
刘景林, 王帅夫
(西北工业大学自动化学院,陕西西安 710072)
0 引言
混合式步进电机是一种能将数字脉冲转换为模拟量输出的机电元件,在电机参数确定时,转子位移量只与输入脉冲数有关,具有较高的控制精确度且控制方法简单,起停迅速,工作可靠。基于以上优势,步进电机一般采用直接驱动方式,可以消除存在于传统驱动方式(带减速机构)中的间隙、摩擦等不利因素,增加伺服刚度,从而显著提高伺服系统的终端合成速度和定位的精确度。因此,混合式步进电机广泛应用于数控系统、机器人等高精确度控制领域[1-3]。
随着工业应用的不断深入和相关技术的发展,对混合式步进电机的性能要求日益提高。开环时存在的低频转矩脉动,高频失步等问题越来越突出。此外,在数控加工领域,空间立体加工是发展趋势,因此需要多个轴向相互配合完成。各个轴向如何协调动作,减小加工的轮廓误差,这就对插补算法提出了更高的要求。以上都是多步进电机伺服系统需要研究的问题。
不同于一般类型的电机,混合式步进电机结构特殊,内部各控制变量高度非线性且相互耦合,难于用简单的数学模型对其进行描述。因此,传统的经典控制方法难以达到高精确度、高时效性的控制效果[4]。近年来,智能控制技术的发展为解决混合式步进电机的上述问题提供了新的控制方法。模糊控制方法具有善于利用经验知识、推理能力强等特点[5-6];神经网络控制方法具有非线性映射、自学习等能力[7];自适应控制方法则能对被控对象进行在线辨识,这些方法均已应用于混合式步进电机的控制中。然而,智能控制技术一般存在计算量大、迭代次数多、学习收敛速度慢等缺陷[8]。
20世纪末,学者们认识到情感在人的认知行为中的重要作用。其中Moren等人于2000年提出基于神经生理学的大脑情感学习(brain emotional learning,BEL)模型[9]。该模型效仿大脑中杏仁核(Amygdala)与眶额皮质(orbitofrontal)间信息传递方式的计算模型,简称A-O(amygdala-orbitofrontal)系统。此后,Lucas等人提出基于BEL模型的智能控制器(brain emotional learning based intelligent controller,BELBIC)[10],并将该控制器应用于开关磁阻电机[11-12]、感应电机[13]、永磁同步电机[14-16]等电机的速度控制和磁通控制,使得电机的速度响应能力和抗干扰性能都得到了提高。
本文将BEL模型智能控制方法学习能力强、计算简单、对外界干扰不敏感,特别是对非线性和时变的被控对象有较好的适应能力等特点,应用于对混合式步进电机的控制,从而减小低频段的转矩脉动和高频时的失步现象。
在数控机床加工过程中,通常需要多个随动轴相互配合。然而,目前的步进电机伺服系统大多为对单个电机的控制[17-18],没有考虑各轴上电机之间的协调运动,带来较大的轮廓误差。针对这个问题,提出一种混合式步进电机的自适应插补算法。采用变步长的思想,在保证误差精度的情况下,快速进行插补。并且通过把各轴上须行进的位移转换为该轴上步进电机所需的脉冲,从而协调各轴上电机的运动,达到相互配合的目的,减小轮廓误差。该插补算法不存在累积误差,只有弓高误差,插补精确度较高。
1 多步进电机伺服系统
多步进电机伺服系统的结构框图如图1所示。主要包括以下几个部分,执行机构所采用的电机为两相混合式步进电机;控制部分,分别有位置控制和电流控制;功率驱动部分,为功率管H桥电路;检测部分,包括位置检测和电流检测;插补控制,这部分主要负责运行插补算法,协调各电机间相互运动,为步进电机提供脉冲。
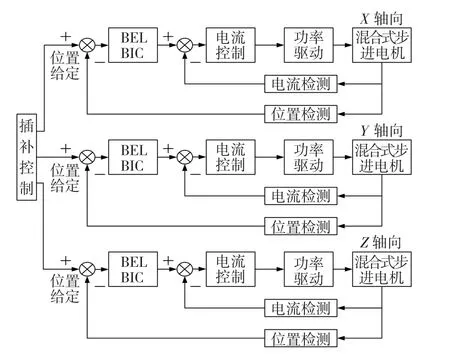
图1 多步进电机伺服系统结构框图Fig.1 Block diagram of multi-stepping motor servo system
2 大脑情感学习模型
大脑情感学习模型是建立在模仿杏仁核与眶额皮质层的生理结构的基础上[9],其基本结构如图2所示。
模型中各部分的作用如下:丘脑主要对感知输入信号进行预处理,如过滤或降低噪声。感知皮质主要对丘脑输出的信号进行进一步的细化和辨别。杏仁核和眶额叶皮层是整个模型中关键。杏仁核主要负责大脑的情感学习过程,用来感知情绪的刺激。而眶额皮质层对杏仁核内进行的学习过程起监督作用,防止出现过学习或者欠学习的情况。

图2 大脑情感学习模型基本结构Fig.2 Basic structure block diagram of BELBIC
BEL模型模拟了A-O组织之间的信息传递方式,对应每个刺激输入信号,杏仁核和眶额皮质层内都有对应的节点接收。刺激信号包括感官输入信号S、奖励信号(reward,REW)以及丘脑信号Ath。丘脑接收感官输入信号S中的最大值,并且只把这个值输送到杏仁核部分,即

杏仁核接收感官输入信号S、奖励信号REW以及丘脑信号Ath,并对其进行学习。假设这些信号的个数为n,那么

式中:Vi为杏仁核中节点Ai的权值。杏仁核内情感的学习过程即为权值的动态调节过程。权值Vi对应奖励信号REW和节点Ai的差值成比例,其学习速度为
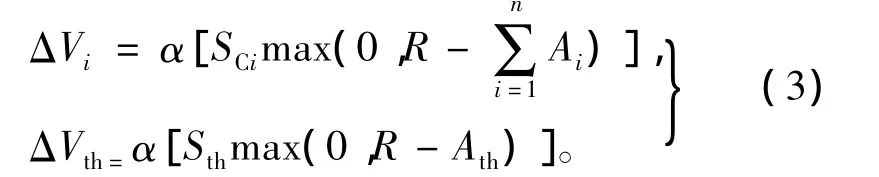
式中:R为奖励信号REW,α为调节系数,它是影响杏仁核学习速度的关键因素。从式(3)可以看出,ΔVi与SCi的符号保持一致,即与感官输入信号Si的符号保持一致。
当Si≥0时,则 ΔVi≥0,Vi增加,直至Vi≤R/Si;当Si<0时,则 ΔVi<0,Vi减小,直至Vi>R/Si。
眶额皮质层的作用是当学习过程不合适时进行适当的调节。它接收来自感知皮质和杏仁核的信号,其节点输出为
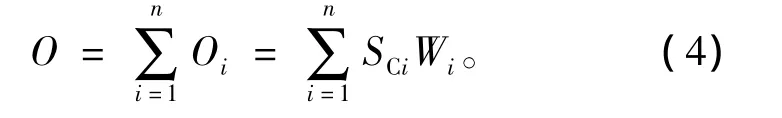
其中:Wi为眶额皮质层中节点Oi的权值。其学习速度为

式中:β为调节系数。E'为不含丘脑刺激信号下的杏仁核的输出减去节点O的值,即

从式(5)中可以看出,学习速度ΔWi可正可负,正值表示抑制杏仁核的学习,负值表示刺激杏仁核的学习。通过减小奖励信号与E'之间的差值,使杏仁核朝期望值学习。
整个BEL模型的输出为

式中:A为杏仁核的输出;O为眶额皮质层的输出;n为组织内的节点个数(即感官输入个数)。
3 步进电机的大脑情感学习控制
根据大脑情感学习控制机理,建立混合式步进电机的控制系统结构,如图3所示。

图3 基于BEL模型的混合式步进电机控制系统结构Fig.3 Hybrid stepping motor control system based on BEL model
把BEL模型应用到实际系统当中时,首先需确定感官输入函数S和情感暗示函数(亦即奖励信号)REW的形式。
本文根据混合式步进电机的特性,选取的S和R如式(8)、式(9)所示,有

式中:u为控制器输出;e为误差。K1至K4为权值调节系数。
在该控制系统中,利用混合式步进电机的反电动势来检测位置。该方法不用安装位置传感器,减小了电机的体积和成本,更为简便和经济。
两相混合式步进电机基于齿层比磁导法的简化磁网络模型如图4所示,模型中忽略了漏磁的影响。齿层比磁导不是一个常数而是定、转子齿中心线相对位置的一个变量,而且和齿层的结构、尺寸有关。它是一个关于齿高、齿宽、齿距、气隙和定转子齿相对位置的函数。每极下的磁导主要由气隙磁导、定转子齿磁导和定转子轭磁导组成。

图4 两相混合式步进电机简化的磁网络模型Fig.4 Simplified magnetic network model of two-phase hybrid stepping motor
图4中 Λa1、Λb1、Λc1、Λd1为I端铁心相应极下的磁导;Λa2、Λb2、Λc2、Λd2为II端铁心段相应极下的磁导。这些磁导参数都是转子位置角的周期函数。Λm为永磁体内部磁导,Fm为永磁体磁势。
各磁路磁导表达式为
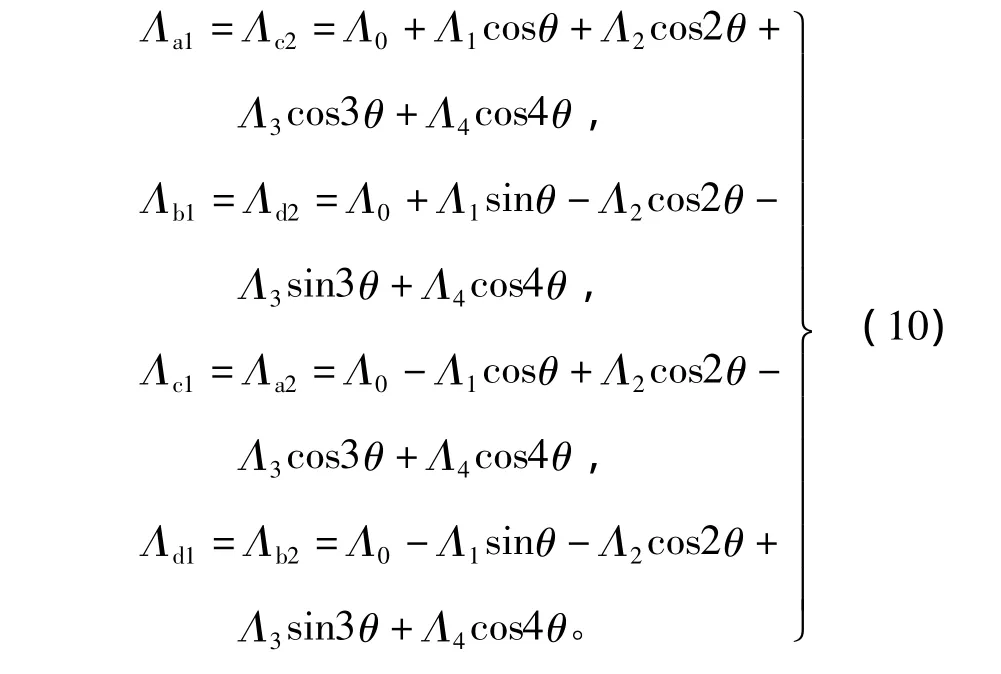
式中:Λ0为一端铁心段一相两个极齿层磁导的平均分量;Λ1为一端铁心段一相两个极齿层磁导的基波分量;Λ2、Λ3、Λ4为一端铁心段一相两个极齿层磁导的各谐波分量。
通过分析不通电励磁时和某一相通电励磁时的磁场变化情况,得出各情况下的磁通表达式。
当电机未通电励磁时,则气隙磁通为永磁体产生的磁通为
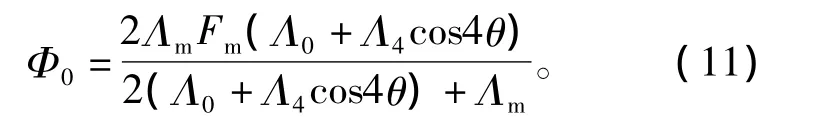
当电机按A、B、/A、/B的顺序逐一通电时,参照图4所示的模型,利用节点法分析,Φ1、Φ2、Φ3、Φ4为

当步进电机采用双四拍通电方式即AB→/AB→/A/B→A/B时,则总磁通Φ为
式中:Fj=N×Ij;j=a,b,c,d;N为绕组线圈匝数;Ij为定子绕组相电流。
则反电势为

当定子绕组开路,则Im=0,Im是定子绕组各相电流的有效值。电机被拖动旋转时,反电势的值仅含式(14)中的第一项,如图5(a)所示;而当电机通电时,定子绕组和转子永磁体共同作用,它们的叠加反应了混合式步进电机反电动势的变化,如图5(b)所示。

图5 反电势波形Fig.5 Back electromotive force waveform
4 自适应插补算法
本文中提出一种自适应的变步长插补算法,它不固定每一步的长度,而是根据下一个插补点处的曲率和挠率,在保证轮廓误差的情况下,自动调节插补的步长,这样既保证了精确度也加快了速度。
一般空间曲线c的参数方程为

在一个插补周期内,Δl的表达式为

式中:i=0,1,2,…,n-1需满足 Δt=ti+1-ti>0。
如果空间曲线在定义域内都有连续二阶可导,曲率κ(t)、挠率τ(t)存在并连续,则可由弦长代替弧长,即

令f(t)=|c’(t)|,用泰勒公式可以得到
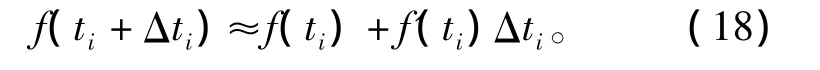
把式(18)代入式(17)中,并保证Δti>0的情况下,得到

通过上式计算出Δti,代入参数方程式(15),从而得出各轴上的插补分量。
步进电机角位移量与步距角θ和脉冲数相关,当电机参数确定时,其转过的角度只与脉冲数成比例。因此,将各轴上的插补分量通过步进电机的脉冲当量求取各轴上所需的脉冲数。
本文采用的自适应插补算法,用折线l逼近曲线c时,每个插补点均落在曲线上,因此不存在累积误差,只有弓高误差。弓高误差即为轮廓误差ε。
最大插补步长Δlimax与轮廓误差ε之间的关系可表示为

式中:R为插补点处的曲率半径。
5 实验结果
应用文中的自适应插补算法对方程为2z=(x2/100)-(y2/400)的空间曲面进行插补,如图6所示。

图6 空间曲面插补仿真结果Fig.6 Simulation results of surface interpolation
对于零件上的被加工曲面,不可能一次走到加工完,通常只能按一定的加工路径逐行进行,图6中曲面上的线段,是按照参数方程为c(t)={t,a,(4t2-a2)/800}进行插补,a逐一变化则生成曲面上的插补线段族。
图7为使用本文的插补算法和使用直接函数法[19]插补的轮廓误差的数据对比(取步长为1 mm)。实线为使用直接函数法时的轮廓误差曲线,虚线为使用本文中的自适应插补算法时的轮廓误差曲线。可以看出,本文的方法能减小插补过程中的轮廓误差,而且插补步数少,能使插补过程更加迅速。

图7 两种方法轮廓误差对比Fig.7 Contour error comparison of two methods
图8所示为使用本文中的大脑情感学习控制(BELBIC)与PID方法下,步进电机速度响应的对比仿真图。可以看见,大脑情感学习控制下步进电机的速度响应更快,超调更小,提高了电机性能。
在自行研发的数控系统上进行实验。该系统是基于DSP2812为控制核心。实验参数及所用步进电机的参数如下:步进电机工作在整步运行状态下,电流为0.6 A,电压25 V,相电阻R=30 Ω,电感L=0.037 H,转子齿数Zr=50,极对数P=2。
图9所示为实验现场,图10为实测自适应插补算法的输出脉冲波形,验证了该算法的有效性。
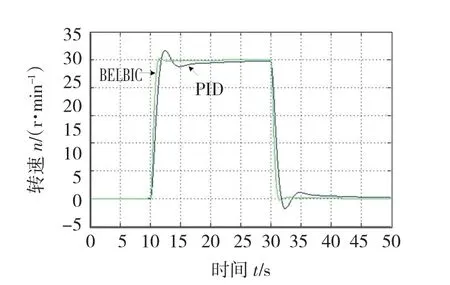
图8 BELBIC与PID控制速度响应曲线Fig.8 Velocity response curve under BELBIC and PID control

图9 试验现场Fig.9 Experimental site

图10 实际输出脉冲波形Fig.10 Output pulse waveform
图11所示为使用大脑情感学习控制(BELBIC)与PID控制下的两相混合式步进电机的矩频特性对比。可以看见BELBIC的控制效果较好,在较宽频率内,步进电机输出的转矩稳定,鲁棒性较强。
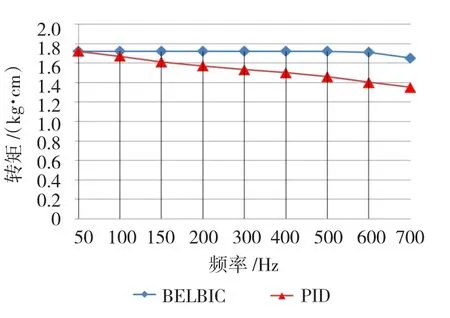
图11 BELBIC与PID控制下的矩频特性Fig.11 Torque-frequency characteristics under BELBIC and PID control
6 结语
针对两相混合式步进电机,建立了基于大脑情感回路的人工情感智能模型,并在此基础上设计了基于BEL模型的智能控制器,应用于步进电机的位置控制当中。它能较好的适应混合式步进电机强耦合、非线性的特点,并且具有运算速度快、学习能力强等优点,实验结果表明,BELBIC能够使步进电机运行的更平滑,鲁棒性更强。
插补算法是数控加工系统的关键部分之一,它的好坏将影响到系统的加工精确度和实时性。本文中提出的自适应插补算法适用于对以参数方程表示、且Frenet标架存在的正则曲线的拟合加工。因为插补点均落在曲线上,所以不存在累积误差而只存在弓高误差。在计算曲率半径时,误差精确度作为一项参数代入计算。因此每步的插补均能保证在误差要求范围内。该算法在得到参数变化值之后,能够直接通过参数方程知道各轴上需插补的进给量,然后转换成脉冲数,直接输出给各轴刀具的执行机构——步进电机,该算法比较符合步进电机的特点。.
[1]CHEN W D,YUNG K L,CHENG K W.Profile tracking performance of a low ripple hybrid stepping motor servo drive[J].IEEE Proceedings Control Theory and Applications,2003,150(1):69-76.
[2]ELSODANY N M,REZEKA S F,MAHAREM N A.Adaptive PID control of a stepper motor driving a flexible rotor[J].Alexandria Engineering Journal,2011,50(2):127-136.
[3]陈卫东,容启亮.基于鲁棒自适应控制策略的混合型步进电机低速伺服控制性能(英文)[J].Transactions of Nanjing University of Aeronautics&Astronautics,2007,24(1):8-16.
CHEN Weidong,RONG Qiliang.Robust adaptive control scheme for improving low-speed profile tracking performance of hybrid stepping motor servo drive[J].Transactions of Nanjing University of Aeronautics&Astronautics,2007,24(1):8-16.
[4]许淑辉.步进电动机恒流斩波驱动器的设计[J].华侨大学学报:自然科学版,2002,23(4):350-353.
XU Shuhui.Designing a driver of constant current and chopped mode for a stepping motor[J].Journal of Huaqiao University:Natural Science,2002,23(4):350-353.
[5]史敬灼,徐殿国,王宗培.模糊控制步进电动机位置伺服系统[J].电工技术学报,2001,16(3):20-23.
SHI Jingzhuo,XU Dianguo,WANG Zongpei.Stepping motor position servo system with fuzzy control[J].Transactions of china electrotechnical society,2001,16(3):20-23.
[6]赵鸿宇.二相混合式步进电动机模糊控制位置伺服系统[J].黑龙江工程学院学报,2005,19(2):28-31.ZHAO Hongyu.Two-phase hybrid stepping motor fuzzy position servo system[J].Journal of Heilongjiang Institute of Technology,2005,19(2):28-31.
[7]HASANIEN H M.FPGA implementation of adaptive ANN controller for speed regulation of permanent magnet stepper motor drives[J].Energy Conversion and Management,2011,52(2):1252-1257.
[8]JAMALI M R,ARAMI A,DEHYADEGARI M,et al.Emotion on FPGA:Model driven approach[J].Expert Systems with Applications,2009,36(4):7369-7378.
[9]MOREN J B C.A computational model of emotional learning in the amygdale[M].Cambridge:The MIT Press,2000:165-173.
[10]PARSAPOOR M,LUCAS C,SETAYESHI S.Reinforcementrecurrent fuzzy rule based system based on brain emotional learning structure to predict the complexity dynamic system[C]//Third International Conference on Digital Information Management,Nov.13-16,2008,London,UK.2008:25-32.
[11]DARYABEIGI E,ARAB Markadeh G,LUCAS C,et al.Switched reluctance motor(SRM)control,with the developed brain emotional learning based intelligent controller(BELBIC),considering torque ripple reduction[C]//IEEE International E-lectric Machines and Drives Conference,May 3-6,2009,Miami,USA.2009:979-986.
[12]DEHKORDI B M,PARSAPOOR A,MOALLEM M,et al.Sensorless speed control of switched reluctance motor using brain emotional learning based intelligent controller[J].Energy Conversion and Management,2011,52(1):85-96.
[13]DARYABEIGI E,MARKADEH G A,LUCAS C.Simultaneously,speed and flux control of a induction motor,with brain emotional learning based intelligent controller(BELBIC)[C]//IEEE International Electric Machines and Drives Conference,May 3-6,2009,Miami,USA.2009:894-901.
[14]DARYABEIGI E,MARKADEH G A,LUCAS C.Interior permanent magnet synchronous motor(IPMSM),with a developed brain emotional learning based intelligent controller(BELBIC)[C]//IEEE International Electric Machines and Drives Conference,May 3-6,2009,Miami,USA.2009:1633-1640.
[15]FARD F T P,SHAHGHOLIAN G,RAJABI A,et al.Brain emotional learning based intelligent controller for permanent magnet synchronous motor[C]//International Symposium on Parameterized and Exact Computation,Dec.13-15,2010,Chennai,India.2010:989-993.
[16]GHAEBI Panah P,SHAFIEI A,PARSA Pour A,et al.Velocity control of a PMLSM using a brain emotional learning based intelligent control strategy[C]//IEEE International Conference on System Engineering and Technology,June 27-28,2011,Shah Alam,Malaysia.2011:47-52.
[17]史敬灼,徐殿国,王宗培.混合式步进电动机伺服系统研究[J].电工技术学报,2006,21(4):72-78.
SHI Jingzhuo,XU Dianguo,WANG Zongpei.Study of the hybrid stepping motor servo system based on DSP[J].Transactions of China Electrotechnical Society,2006,21(4):72-78.
[18]AGUILAR L,MELIN P,CASTILLO O.Intelligent control of a stepping motor drive using a hybrid neuro-fuzzy ANFIS approach[J].Applied Soft Computing,2003,3(3):209-219.
[19]唐学飞,姚传维,王新安.数控系统直接函数法圆弧插补算法的改进[J].机床与液压,2004,(4):87-88.
TANG Xuefei,YAO Chuanwei,WANG Xinan.Improved direct function method for circular interpolation of numerical control system[J].Machine Tool&Hydraulics,2004,(4):87-88.

