博弈模型在复杂系统连锁故障预防的应用
曹然, 金鸿章, 冯丽媛
(1.哈尔滨工程大学自动化学院,黑龙江哈尔滨150001;2.东北农业大学 电气与信息学院,黑龙江 哈尔滨150030)
0 引言
复杂系统故障传播、分析已成为研究热点。文献[1]提出了利用模糊灰关联分析方法对复杂系统故障树进行分析,从而找出系统的薄弱环节。文献[2]系统的故障以模糊的变量形式表达,提出了基于Takagi-Sugeno模型的故障树分析方法用于分析复杂系统的可靠性。故障树分析法存在以下问题:其静态结构导致它不能用来分析连锁性故障;故障关系的确定性导致故障树通常适合于逻辑关系清晰、故障机理确定、相对简单的系统,不能满足复杂系统故障分析的要求[3]。贝叶斯网络方法的因果关系在描述故障传递关系时不能表示其动态传播规律[4]。文献[5]和文献[6]研究发现状态参量与系统的故障演化过程之间有着某种对应关系。基于协同学的观点,系统处于相变点的状态参量可分为快驰豫变量和慢驰豫变量两类,慢驰豫变量被称为系统的序参量,他主宰着系统演化的方向。因此,确定系统演化过程中的序参量对子系统的影响是关键。在复杂系统中存在着各子系统的独立运动,也存在着各子系统之间的协同作用。在复杂系统脆性[7]被激发之前,子系统之间的关联相对较弱,他们之间的关联度不能束缚子系统的独立运动,此时子系统的独立运动起主导作用。随着序参量的不断变化,当某子系统靠近临界点时,子系统之间的关联逐渐增强,当某一序参量达到阈值时,子系统之间的关联起主导作用。因此,在复杂系统中出现了由关联决定的各子系统间的协同作用。此时,若某子系统出现故障,在子系统间的协同作用下,整个复杂系统可能会发生连锁性故障。考虑到多个序参量之间存在的竞争及复杂系统故障传播的动态性,本文提出了一种基于协同学原理的非合作博弈模型,用来分析复杂系统连锁性故障的过程,预测避免系统连锁性故障的方法。
1 基于协同学的非合作博弈模型
1.1 博弈描述
在临界点处,系统中往往同时存在多个序参量,每一个序参量都企图主宰系统的格局,该过程实质上是一种非合作博弈行为,将子系统中的多个序参量作为博弈模型中的参与人,序参量在某一时刻的值就是其可选策略。该模型为一个三元组,Γ=(N,S,ui),其中S为有限的非空策略集合,S={si|si=(xi,t),i=1,…,N},xi为序参量 i的值,xi∈[,],其中和分别表示xi的最小和最大临界阈值。xi取值越大,子系统的有序度越高;xi取值越小,子系统的有序度越低。ui为每个序参量i∈N得益函数。得益函数ui为策略集合S到实属集合R的映射。当且仅当u()>u()时,序参量i在主宰系统格局的几率高于的。
在构造博弈模型的过程中,除了要定义参与人、参与人的策略集合以外,还有非常重要的一个步骤——定义每个参与人的支付函数。
1.2 支付函数设计
每个序参量的目标是尽量改变自身的有序度以主宰系统格局,序参量的有序度越大,它对系统的有序性贡献越大。随着序参量的连续变化,系统内的几个序参量的地位和作用也在发生着变化,在某段时间内有序度变化幅度越大的序参量越有机会左右系统的格局。因此,将每个序参量i从t-1时刻到t时刻这段时间内,它的有序度之差的绝对值定义为每个序参量i的得益函数为
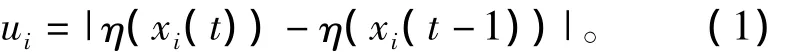
式中:η(xi(t))表示序参量i的有序度;xi(t)表示t时刻序参量i的值。

将式(2)代入式(1),得

序参量i的临界阈值一定,从t-1时刻演化至时刻t,序参量的值变化越大,他就越有机会主宰他所在子系统的格局,因此,式(3)作为序参量i的得益函数是合理的。


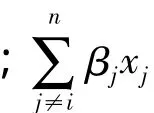

根据式(4)和式(5),得出xi(t)-xi(t-1)的公式为

将式(6)代入式(3),最终得出序参量i的得益函数公式为

1.3 Nash均衡存在性
定义:在n个序参量参与的非合作博弈中,序参量的策略组合{,…},满足对每个序参量i是针对于其他 n-1个序参量所选{,…,,,…}的最优策略,则策略组合是该序参量博弈的一个Nash均衡,描述Nash均衡为

对于所有序参量都成立,现在问题就转化成为求maxui最优解的问题。求解最优策略等价于寻找博弈模型中的Nash均衡点。
引理序参量博弈模型的Nash均衡点存在。




根据上式,解得序参量i的纳什均衡解为


1.4 博弈模型求解
对于拥有多个子系统的复杂系统来说,由于策略的多种组合,寻找均衡点非常耗费时间,在这种情况下,当处理复杂性问题时,可以应用遗传算法(genetic algorithm,GA),他可以简化均衡求解过程。该算法已多次被证明成功应用到博弈论中[8-9]。本文设计的遗传算法解算模型可分为如下3个步骤:1)将基于协同学的非合作博弈模型映射为遗传算法中的种群模型和基因模型,设定初始种群;2)根据相应的约束规则执行选择、交叉、变异,产生新种群;3)判断每个个体的最终适应度值,选择最优个体作为本解算模型的最终结果。
本遗传解算模型将每个参与人的策略集合映射为个体的多条染色体(基因),染色体采用实数编码。对于选择算子,采用随机遍历抽样方法;对于交叉算子,采用单点交叉;对于变异算子,采用离散变异。为实现各参与人的利益最大化,达到均衡目标,设计遗传算法的适应度函数为

2 应用实例
为了验证前面所提出的博弈模型,本文以海湾JB-QG/QT-GST9000火灾报警控制器为例进行说明,该控制器具有容量大、灵活模块化结构、全面自检等功能,是新一代火灾报警控制器。将JB-QG/QT-GST9000火灾报警控制器应用于某船舶的消防联动控制中,该船共分为10个水密区,控制器可使用本地网卡,通过船舶专用电缆网络实现多控制器的联网,每个从机对不同水密区进行联动控制,其网络拓扑结构及探头分布如图1所示。
由图1可知,该控制网络互联了5台从机(子系统),从机1负责1、2、3水密区的消防联动控制,5条回路共带339个探头;从机2负责4、5水密区的消防联动控制,5条回路共带317个探头;从机3负责6水密区的消防联动控制,2条回路共带114个探头;从机4负责7水密区的消防联动控制,4条回路共带292个探头;从机5负责8、9、10水密区的消防联动控制,4条回路共带237个探头。系统内各从机的火警、反馈、故障等信息是可交换、共享的,网络中的每一台从机均可完成对网络中任意设备的控制。复杂度[10]的定义公式为

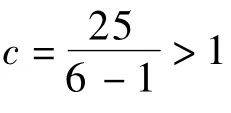

图1 火灾报警控制器网络拓扑结构图Fig.1 Topology of fire alarm controller
由于系统的复杂性,很难区分各种参量随时间变化的快慢程度,只能依据序参量的特点来进行选择:1)引入的序参量是宏观参量,用于描述系统的整体性;2)序参量是微观子系统集体运动的产物,合作效应的表征和度量;3)序参量支配子系统的行为,主宰着系统演化过程。基于以上特点各子系统序参量可选用监控功耗增量、报警功耗增量和从机负载增量,分别表示为ΔM,ΔA和ΔL。根据《JBQG-QT-GST9000火灾报警控制器(联动型)安装说明书》,该火灾报警控制器的监控功耗和报警功耗公式为:M=基本功耗70 W+单块回路板监控功耗6 W(484个总线设备)×回路数;A=基本功耗7 0 W+单块回路板报警功耗7 W(484个总线设备)×回路数。其中,M表示监控功耗,A表示报警功耗。根据该公式计算出各从机的M、A和负载值,见表1。根据表1可得出各从机ΔM、ΔA和ΔL的临界阈值,见表2。遗传算法的初始参数设置如下:种群数为100,变异概率为0.01,交叉概率为0.7,遗传代数为100。模型中的自身发展系数和合作系数设置如下:α1=0.4,α2=0.4,α3=0.2,β1=0.4,β2=0.4,β3=0.2。

表1 从机1~5的M、A和负载数据信息Table 1 Data of M,A and the number of load in subsystem 1 to 5

表2 ΔM、ΔA和ΔL临界阈值数据信息Table 2 Critical threshold of ΔM,ΔA and ΔL
从机1~5独立运行,若从机2靠近临界点,其部分功能故障,使得从机2与其他从机关联作用增强,此时从机3分担从机2的信息显示、信息查询、信息打印等工作,通过GA得寻优结果如图2所示。由图2可知算法收敛,纳什均衡点为=3.566 4,x=40.534 3=314.796 9,显然此时序参量ΔM最接近其临界阈值,他使得从机3与其他从机关联作用增强。由于长时间负载工作,当从机3靠近临界点时,其部分功能故障,若从机1分担从机2和从机3的信息显示、信息查询、信息打印等工作,通过GA得寻优结果如图3所示。

图2 遗传算法优化过程(从机2故障)Fig.2 Optimization process of genetic algorithm(subsystem 2 fails)

图3 遗传算法优化过程(从机2和3故障)Fig.2 Optimization process of genetic algorithm(subsystem 2 and 3 fails)
3 结语
本文在讨论状态参量与系统的故障演化过程存在某种对应关系的基础上,基于协同学观点,针对复杂系统故障传播的动态性,在复杂系统故障预测中引入博弈论思想,提出了一种基于协同学的非合作博弈模型;将子系统的序参量映射为博弈中的参与人,利用序参量之间既有竞争也有合作特点。对非合作博弈模型进行了求解。仿真实验中,通过对故障传播过程研究,给出了避免复杂系统发生连锁性故障的预防方法。本文提出的方法在船舶的消防联动控制的火灾报警控制中得到了应用。
[1] 周真,马德仲,于晓洋,等.模糊灰关联分析方法在故障树分析中的应用[J].电机与控制学报,2012,16(3):60 -64.
ZHOU Zhen,MA Dezhong,YU Xiaoyang,et al.Application of fuzzy grey relational analysis in fault tree analysis[J].Electric Machines and Control,2012,16(3):60 -64.
[2] SONG Hua,ZHANG Hongyue,CHAN C W.Fuzzy fault tree analysis based on T-S model with application to INS/GPS navigation system[J].Soft Computing,2009,13(1):31 -40.
[3] DURGA Rao K,GOPIKA V,SANYASI Rao V V S,et al.Dynamic fault tree analysis using Monte Carlo simulation in probabilistic safety assessment[J].Reliability Engineering and System Safety,2009,94(4):872 -883.
[4] SIMON C,WEBER P,EVSUKOFF A.Bayesian networks inference algorithm to implement Dempster Shafer theory in reliability analysis[J].Reliability Engineering and System Safety,2008,93(7):950-963.
[5] 侯胜利,李应红,尉询楷,等.基于系统异常概率模型的故分离自动化方法[J].系统工程与电子技术,2007,29(3):483-487.
HOU Shengli,LI Yinghong,WEI Xunkai.Automatic method for fault isolation based on system abnormity probability model[J].Systems Engineering and Electronics,2007,29(3):483 -487.
[6] 张磊,李行善,于劲松,等.一种基于高斯混合模型粒子滤波的故障预测算法[J].航空学报,2009,30(2):319-324.
ZHANG Lei,LI Xingshan,YU Jinsong.A fault prognostic algorithm based on gaussian mixture model particle filter[J].Acta Aeronautica et Astronautica Sinica,2009,30(2):319 -324.
[7] 荣盘祥,金鸿章,韦琦,等.基于脆性联系熵的复杂系统特性的研究[J].电机与控制学报,2005,9(2):111 -115.
RONG Panxiang,JIN Hongzhang,WEI Qi.Research on the characteristic of complex system based on brittle link entropy[J].E-lectric Machines and Control,2005,9(2):111 -115.
[8] PERIAUX J,CHEN HQ,MANTEL B,et al.Combining game theory and genetic algorithms with application to DDM-nozzle optimization problems[J].Finite Elements Analysis Design,2001,37(5):417-429.
[9] HAUSKEN K.Strategic defense and attack for reliability systems[J].Reliability Engineering and System Safety,2008,93(11):1740-1750.
[10] 金鸿章,韦琦,郭健.复杂系统的脆性理论及应用[M].西安:西北工业大学出版社,2010:22-24.

