一类非仿射非线性系统混合自适应模糊控制
吴勃, 宋建力
(1.哈尔滨理工大学自动化学院,黑龙江哈尔滨150080;2.天津航海仪器研究所,天津300131)
0 引言
自适应模糊控制是非线性控制领域中一种重要的控制方法,广泛用于解决各种复杂非线性系统控制问题[1-7]。Wang等针对一种模型未知的SISO非线性系统首次提出了一种稳定的自适应模糊控制方法[2]。Shi等通过估计增益矩阵分解构造一个间接自适应模糊控制器,解决了MIMO非线性系统中出现的奇异问题[3]。目前大部分自适应模糊控制器仅仅适用于仿射非线性系统,而实际工程系统如飞控系统、化学反应系统等属于非仿射非线性系统。因此,非仿射非线性系统控制器的设计成为非线性控制领域热点研究问题。
近年来,针对非仿射非线性系统的自适应模糊控制器设计的研究已取得了很多成果。根据模糊逻辑系统逼近对象的不同,可以将已有控制器分为两类:直接自适应模糊控制器,即首先利用隐函数定理证明非仿射系统存在最优控制律,然后用模糊逻辑系统直接逼近最优控制律[8-11];间接自适应模糊控制器,利用泰勒级数或者中值定理将非仿射系统转化为仿射系统,然后利用模糊系统逼近仿射系统中未知的非线性函数,结合反馈线性化方法构造控制器[12-14]。仿射非线性系统存在另一种自适应模糊控制设计方案即混合自适应模糊控制器,该控制器有两种构造方法,其一是通过调节因子直接将直接型和间接型两种控制器融合在一起[15],这样能将两种控制器的优点同时利用起来,使系统获得更好的控制效果;其二为构造模糊控制器后,同时采用跟踪误差和预测误差来设计自适应律[7,16],从而提高收敛速度。
以上控制器设计均假设控制方向已知并且通常假设控制方向为正,但是在实际控制系统中大多数情况下控制方向是未知的。当系统控制方向未知时,采用直接自适应模糊控制器设计方案会因为不能确定参数更新方向而无法实现控制器的设计,采用间接自适应模糊控制器设计方案则可能会出现控制器奇异问题。结合文献[13]方法,本文提出一种混合自适应模糊控制方案,该方案同时利用跟踪误差和模型预测误差设计参数自适应律,相比于文献[13],本文设计控制器时不仅考虑了系统存在有界干扰的情况,而且系统具有更快收敛速度。
1 问题描述
考虑一类SISO非仿射非线性模型,即

上式可等价为
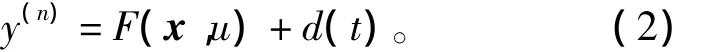
式中:y∈R为系统输出量;u∈R为系统输入量;x=[x1,x2,…,xn]T∈Rn为系统的状态向量;F(x,u)为光滑的未知函数;d(t)为未知但有界的外部干扰。
控制目标设计自适应模糊控制器u(t),使闭环系统输出y跟踪期望信号yd,同时保证闭环系统中所有信号有界。
为完成控制目标,需对系统和期望信号做如下假设。

假设2 期望信号yd及其n阶导数均光滑有界。
定义跟踪误差为e1=yd-y,则跟踪误差向量为e=[e1,…,e1(n-1)]T∈Rn。
为便于设计控制器,首先利用泰勒级数原理将非仿射系统转换为仿射形式,式(1)可以转换为

2 自适应模糊控制器设计
当 f(x)、g(x)已知并且 Δ(x,u)=0,d(t)=0时,则系统存在一个理想控制律,即

选择向量K=[kn,kn-1,…,k1]T使得多项式sn+k1sn-1+…+kn=0的所有的根均位于左半开平面内,由式(3)可得=KTe,即可以使系统误差指数收敛。但是系统模型f(x)、g(x)未知,因此需要用模糊逻辑系统逼近未知函数f(x)、g(x)。
根据模糊逻辑系统的万能逼近特性[2],存在最优逼近参数和满足
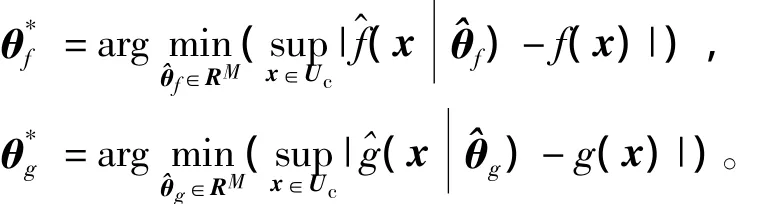
使得
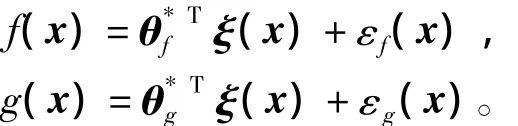

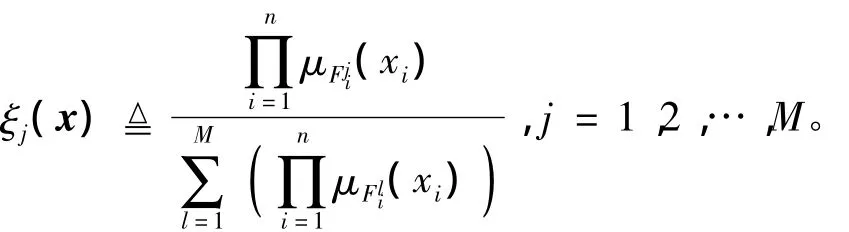
定义参数估计误差为

重新构造模糊控制律有
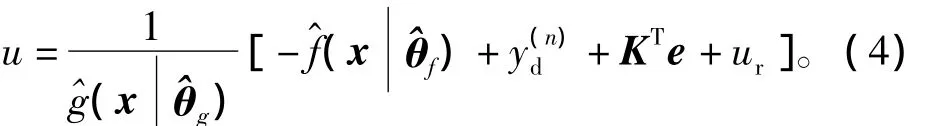
式中,鲁棒控制项ur用来克服由外部干扰、模型转换误差以及模糊逼近误差对系统的影响。
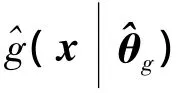
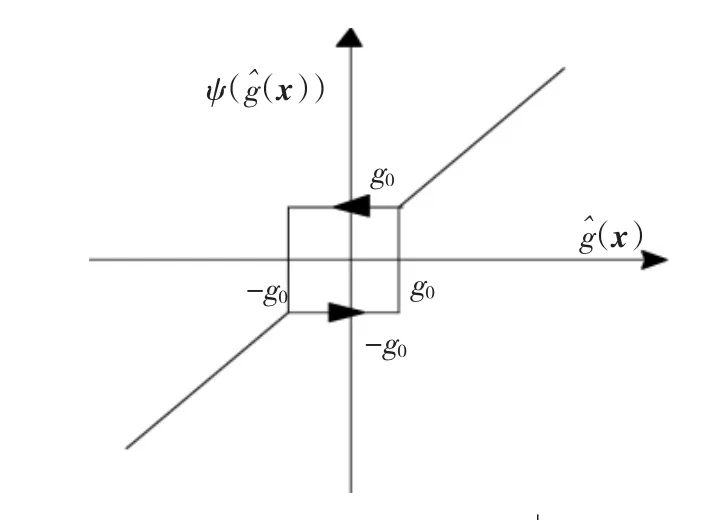
图1 函数ψ((x))与x)关系Fig.1 The relation plot between ψ(g^(x))andg^(xθ^g)
由上述分析可设计模糊控制律为

由式(3)、式(5)可得系统误差方程为

式中:
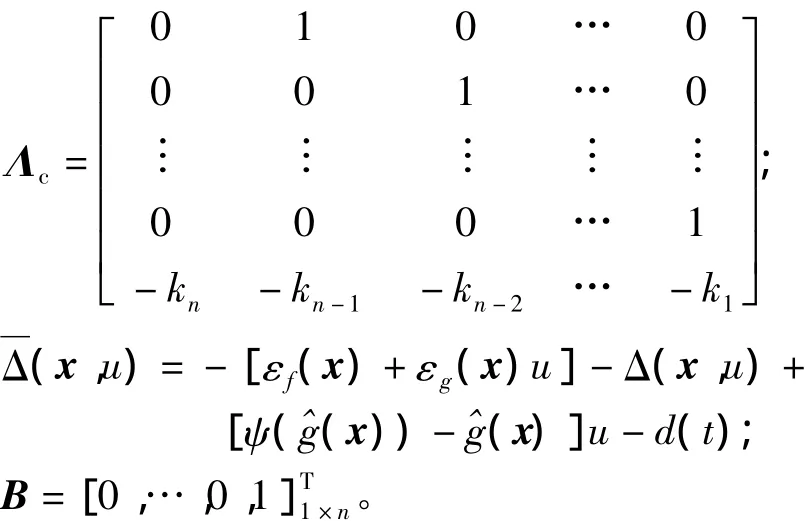
选择向量K=[kn,kn-1,…,k1]T使得多项式sn+k1sn-1+…+kn=0的所有的根均位于左半开平面内,则Λc为稳定矩阵,因此给定一个正定对称矩阵P,存在正定矩阵Q满足Lyapunov方程,即

假设3(x,u)项有界,即满足不等式0≤其中为未知的正常数,(x,u)=1+|u|+ ‖x‖。
文献[13]中仅仅利用跟踪误差分析设计自适应律,为了使系统获得更好的暂态性能即使系统跟踪误差更快收敛,本文设计自适应律时,将同时利用跟踪误差和模型预测误差。由文献[7]分析可知,模型误差可以直接用来调节控制器参数,在引入模型误差的同时,该设计方法并没有带来更复杂的运算,但文献[7]中提出的模型误差预测(t)-(t)要求(t)已知,这在实际应用中是不能满足的,因此根据文献[17],设计预测误差为κ-1(t)--1(t),即有

其中,α为已知的拐点频率。

定理1 考虑系统式(1),采用控制律式(5)以及如下自适应律,可以使系统输出跟踪给定期望信号yr,即跟踪误差收敛到零,并保证闭环系统信号均有界。
自适应律为


证明选取如下Lyapunov候选函数,即

上式对时间求导可得
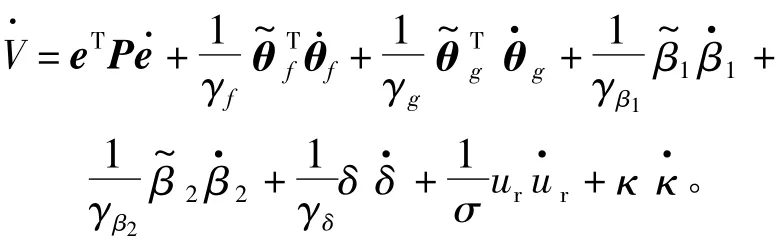
将式(5)~式(13)代入上式有


经整理可得
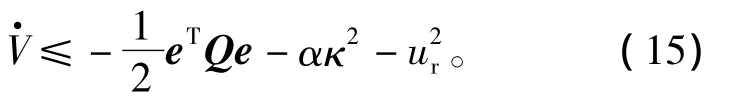
当t→∞时,e→0成立。即系统跟踪误差最终收敛到零。定理1证毕。
3 仿真结果
考虑如下非仿射非线性系统[19],即
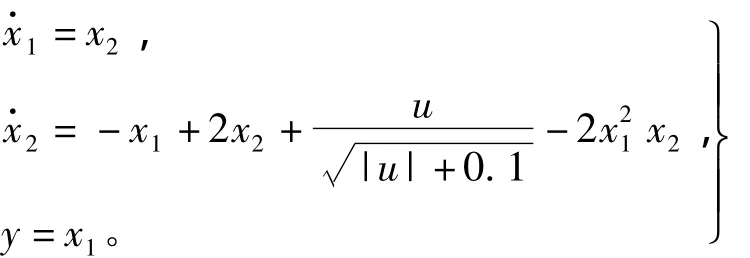
控制目的是使系统的输出y跟踪期望轨迹yr=sin(t)。
参数设计为:θf(0)=[0.1,…,0.149;θg(0)=[0.1,…,0.149;x1(0)=1;x2(0)=0;γf=50;γg=0.01;γβ1=10;γβ2=10;γδ=10;σ =1;α =5;
选择模糊隶属度函数为
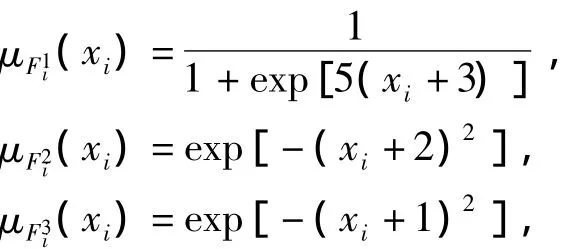
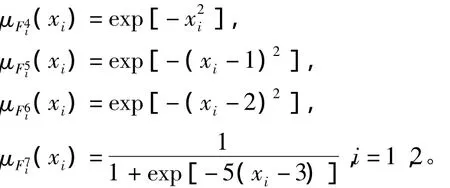
仿真结果如图2~图4所示。

图2 期望输出与实际跟踪曲线Fig.2 The reference trajectory and the system output

图3 跟踪误差Fig.3 The tracking error
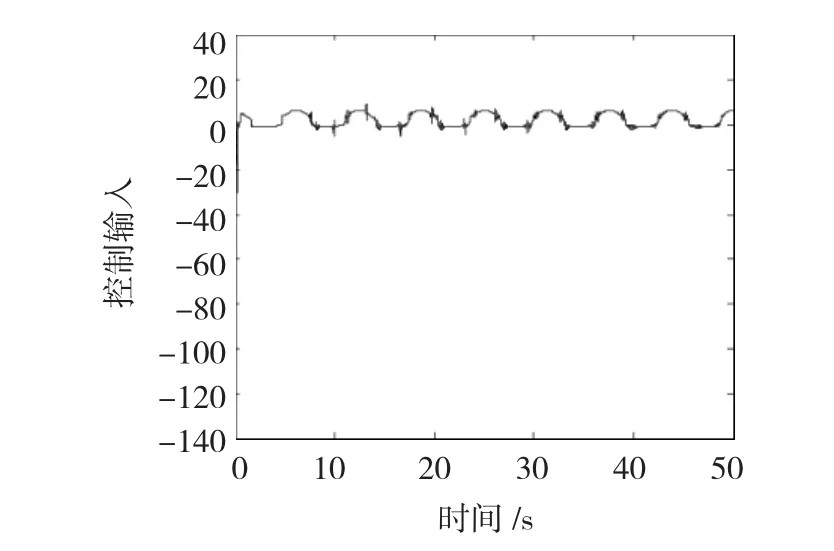
图4 控制输入Fig.4 The control input
图2为系统输出跟踪给定期望信号,其中虚线代表期望信号,实线代表系统输出信号。图3为系统跟踪误差,由图3可知,跟踪误差最终收敛到零,即实现跟踪目的。图4为控制输入,由图4可知,系统控制输入有界。由仿真结果可知,利用所设计的控制器设计方案,可以实现系统输出跟踪给定期望输出信号,跟踪误差最终收敛到零,同时可以保证控制输入有界,验证了系统稳定性。
5 结语
本文针对一类控制方向未知的非仿射非线性系统,提出了一种混合自适应模糊控制算法。利用模糊逻辑系统对仿射系统进行模糊建模,结合跟踪误差和模型预测误差设计了自适应律,理论上证明了系统Lyapunov稳定。仿真结果验证了所提混合自适应模糊控制算法的有效性。
[1] MARKLEY F L.Attitude error representations for Kalman filtering[J].Journal of Guidance,Control,and Dynamics,2003,63(2):311-317.
[2] WANG Lixi.Stable adaptive fuzzy control of nonlinear systems[J].IEEE Transactions on Fuzzy Systems,1993,1(2):146-149.
[3] SHI W X,ZHANG M,GUO W C.Stable adaptive fuzzy control for MIMO nonlinear systems[J].Computers and Mathematics with Applications,2011,62(7):2843 -2853.
[4] CHEN B S,LEE C H,CHANG Y C.H∞tracking design of uncertain nonlinear SISO systems:adaptive fuzzy approach [J].IEEE Transactions on Fuzzy Systems,1996,2(4):32-43.
[5] HSUEH Y C,SU S F.Learning error feedback design of direct adaptive fuzzy control systems[J].IEEE Transactions on Fuzzy Systems,2012,20(3):536 -545.
[6] TONG S C,LI H X.Direct adaptive fuzzy output tracking control of nonlinear systems[J].Fuzzy Sets and Systems,2002,128(1):107-115.
[7] MEHRDAD H,SAEED G.Hybrid adaptive fuzzy identification and control of nonlinear systems[J].IEEE Transactions on Fuzzy Systems,2002,10(2):198 -210.
[8] BOULKROUNE A,M'SAAD M,FARZA M.Adaptive fuzzy tracking control for a class of MIMO nonaffine uncertain systems[J].Neurocomputing,2012,93:48-55.
[9] CHAI T Y,TONG S C.Fuzzy direct adaptive control for a class of nonlinear systems[J].Fuzzy Sets and Systems,1999,103(3):379-389.
[10] HUANG Yishao,WU Min,HE Yong,et al.Decentralized adaptive fuzzy control of large-scale nonaffine nonlinear systems by state and output feedback [J].Nonlinear Dynamics,2012,69(4):1665-1677.
[11] DOUDOU S,KHABER F.Direct adaptive fuzzy control of a class of MIMO non-affine nonlinear systems[J].International Journal of Systems Science,2012,43(6):1029-1038.
[12] LABIOD S,GUERRA T M.Adaptive fuzzy control of a class of SISO non-affine nonlinear systems[J].Fuzzy Sets and Systems,2007,158(10):1126-1137.
[13] LABIOD S,GUERRA T M.Indirect adaptive fuzzy control for a class of nonaffine nonlinear systems with unknown control directions[J].International Journal of Control,Automation and Systems,2010,8(4):903-907.
[14] BECHLIOULIS Charalampos P,ROVITHAKIS George A.Robust adaptive fuzzy control of nonaffine systems guaranteeing transient and steady state error bounds[J].International Journal of adaptive control and signal processing,2012,26(7):576-591.
[15] HUANG Y S,XIAO D S,CHEN X X.H∞trackingbased decentralized hybrid adaptive output feedback fuzzy control for a class of large-scale nonlinear systems[J].Fuzzy Sets and Systems,2011,171(1):72 -92.
[16] COUCEIRO Micael S,FERREIRA Nuno M F,MACHADO J A Tenreiro.Hybrid adaptive control of a dragonfly model[J].Communications in Nonlinear Science and Numerical Simulation,2012,17(2):893-903.
[17] BELLOMO Domenico,NASO David,TURCHIANO Biagio.Composite adaptive fuzzy control[J].IFAC Proceedings Volumes,2005,16:97-102.
[18] SASTRY S,ISIDORI A.Adaptive Control:Stability,Convergence and Robustness[M].Englewood Cliffs:Prentice-Hall,1989.
[19] HOVAKIMYAN Naira,NARDI Flavio,CALISE Anthony J.A novel error observer based adaptive output feedback approach for control of uncertain systems[J].IEEE Transactions on Automatic Control,2002,47(8):1310 -1314.

