QIF和MW模糊度分解方法的比较*

周 巍 冯来平 王永收 姚飞娟

1)中国洛阳电子装备试验中心，洛阳 471003

2)信息工程大学导航与空天目标工程学院，郑州 450052

3)西安测绘研究所，西安 710054

QIF和MW模糊度分解方法的比较*

周 巍1，2)冯来平3)王永收1)姚飞娟1)

1)中国洛阳电子装备试验中心，洛阳 471003

2)信息工程大学导航与空天目标工程学院，郑州 450052

3)西安测绘研究所，西安 710054

基于准电离层方法和Melbourne-Wübbena(MW)方法，选择不同长度的基线利用实测数据进行分析，探讨两种方法对不同长度基线的适用性，为实际应用中模糊度分解方法的选择提供依据。

模糊度;准电离层方法;MW组合;高斯拟合;基线

1 引言

GNSS相对定位中，由于双差观测量消除了接收机钟差、卫星钟差以及硬件延迟等误差的影响，使双差模糊度具有整周性质。模糊度分解的过程一般分为两步:首先将模糊度参数与其他未知参数一并进行估计获得模糊度实数解，然后利用实数解及其协方差信息采用统计方法将模糊度实数解固定为整数。模糊度固定技术对于提高定位精度和定位效率具有重要意义［1］，常用的模糊度固定方法有双频P码伪距法、模糊度函数法、最小二乘搜索算法、LAMBDA方法、准电离层方法(QIF)和Melbourne-Wübbena(MW)方法等，其中，QIF方法和MW方法是最主要的两类模糊度分解方法，尤其对于上千千米的超长基线，准电离层方法和MW方法能较好地确保模糊度解算的成功率［2］。在实际应用中，模糊度分解方法的选择主要依据基线的长度、观测时间长短以及观测量类型等。本文介绍了准电离层方法和MW方法的原理，并利用大量实测数据对选择的不同长度的基线进行分析，探讨两种方法对不同长度基线的适用性。

2 Melbourne-Wübbena 方法［2，3］

MW组合观测量L5由双频伪距P1、P2及载波相位L1、L2构成，其表达形式为:

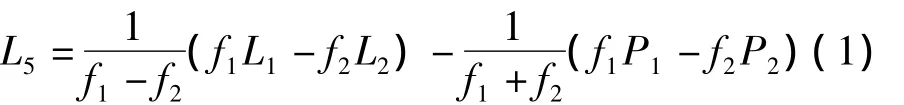
式中f1和f2为载波频率。

双差MW组合可表示为(其中只包含双差模糊度):

双差消电离层组合可表示为:

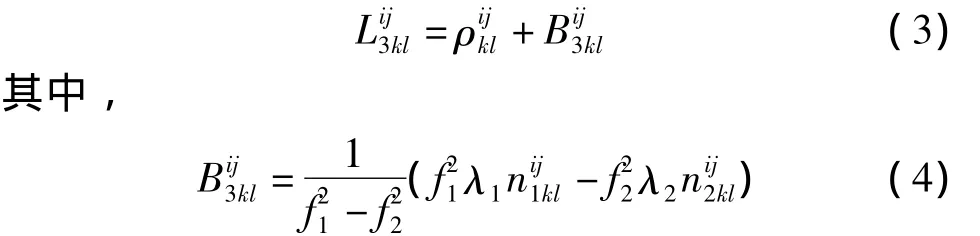
不能表达为，即模糊度不再具有整数性质，但其可以表示为宽巷和窄巷的组合［4］，即

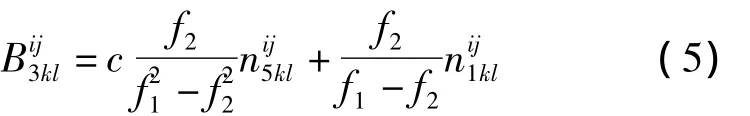
若由MW组合得到宽巷模糊度nij5kl，可进一步得到窄巷模糊度nij1kl。

3 准电离层方法(QIF)

QIF方法不需要双频伪距，但计算过程需要卫星精密星历和双频观测数据［5］。

省略观测站和卫星的标号k、l、i、j，双差观测方程的简化形式为:

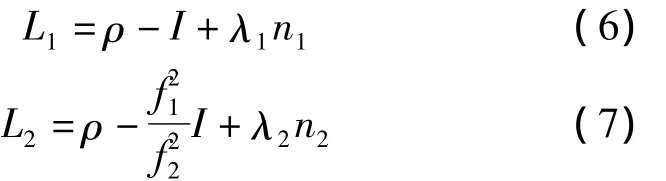
相应的消电离层组合可表示为:

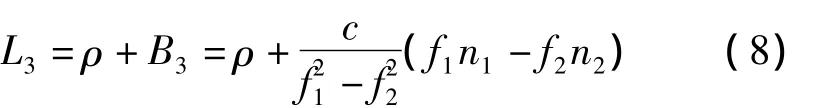
由L1、L2频率模糊度的实数解b1和b2得到消电离层偏差为

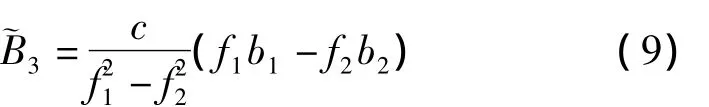
该式可以表示为窄巷周(对应波长为11 cm)的形式:

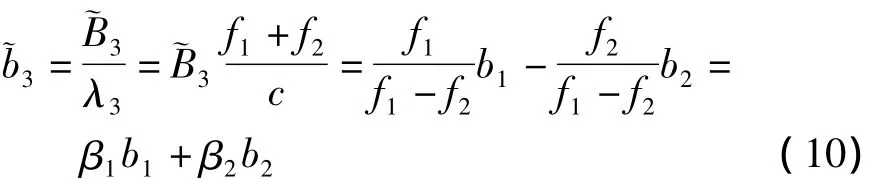
假设n1j和n2j正确固定，消电离层偏差为:

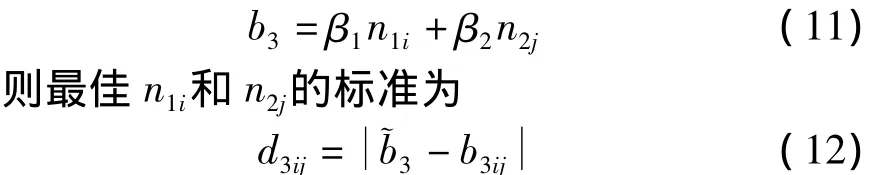
4 方法比较

4.1 高斯拟合法

QIF方法并行处理得到L1和L2模糊度，即得到了窄巷模糊度;而MW方法则是分两步来完成:首先用MW组合得到宽巷模糊度，然后将宽巷模糊度带入消电离层组合得到窄巷模糊度。模糊度实数解与正确固定的整数解之差Δ符合正态分布特性［6］，对于窄巷模糊度，有

统计所有观测数据解算得到的窄巷模糊度，然后用Gauss分布拟合。为了比较两种方法，引入拟合因子的概念，表示Gauss分布拟合函数:

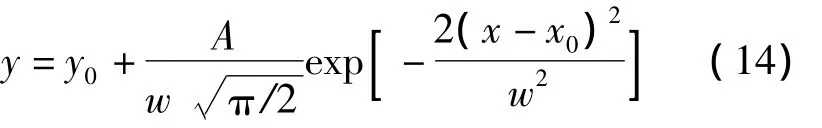
用于拟合的四个参数为y0、A、w和x0，分别代表系统偏差、振幅、均值和方差。拟合因子反映统计结果的拟合程度，定义为:

ν为拟合残差;r为参数个数，此处为4。

4.2 坐标重复性计算

测站坐标精度可通过坐标重复性来反映。对各站所有观测数据做单日解，然后利用多天单日解的重复性作为测量精度评价指标［7，8］，计算公式为:

5 试验分析

5.1 数据选取

选取 5个 IGS参考站(HERS、KIR0、KIRU、NYAL、TROM)7天(2011年 11月 16—22日)的GPS观测数据，数据采样间隔为30 s(图1、表1)。以KIRO为中心形成4条不同长度的基线，数据处理采用Bernese5.0软件。

图1 5个IGS参考站的分布Fig.1 Distribution of five IGS reference stations

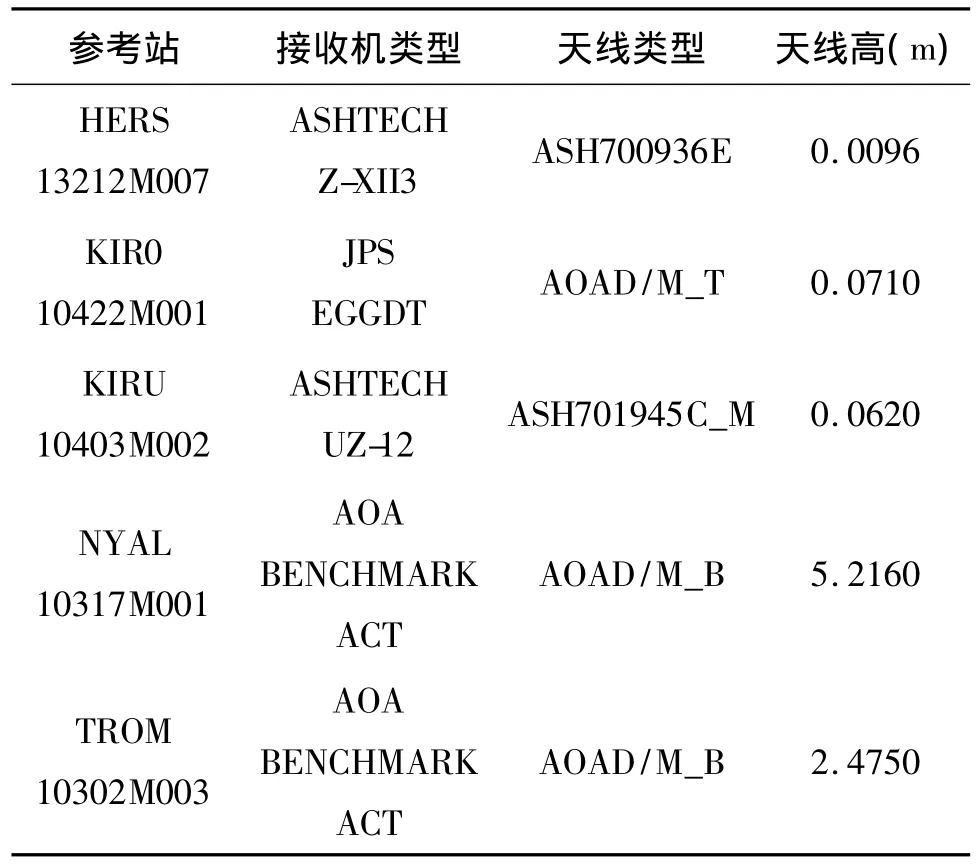
表1 观测站信息Tab.1 Information of reference stations

5.2 计算结果

对基线 KO_KU(KIRO-KIRU)、KO_TM(KIROTROM)、KO_NL(KIRO-NYAL)、KO_HS(KIROHERS)分别采用QIF方法和MW方法得到窄巷模糊度，按照式(11)统计分布特性，结果如图2～5，高斯拟合结果的方差与拟合因子的统计见表2。

图2 KO_KU窄巷模糊度残差分布Fig.2 Distribution of narrow lane ambiguity residual of KO_KU

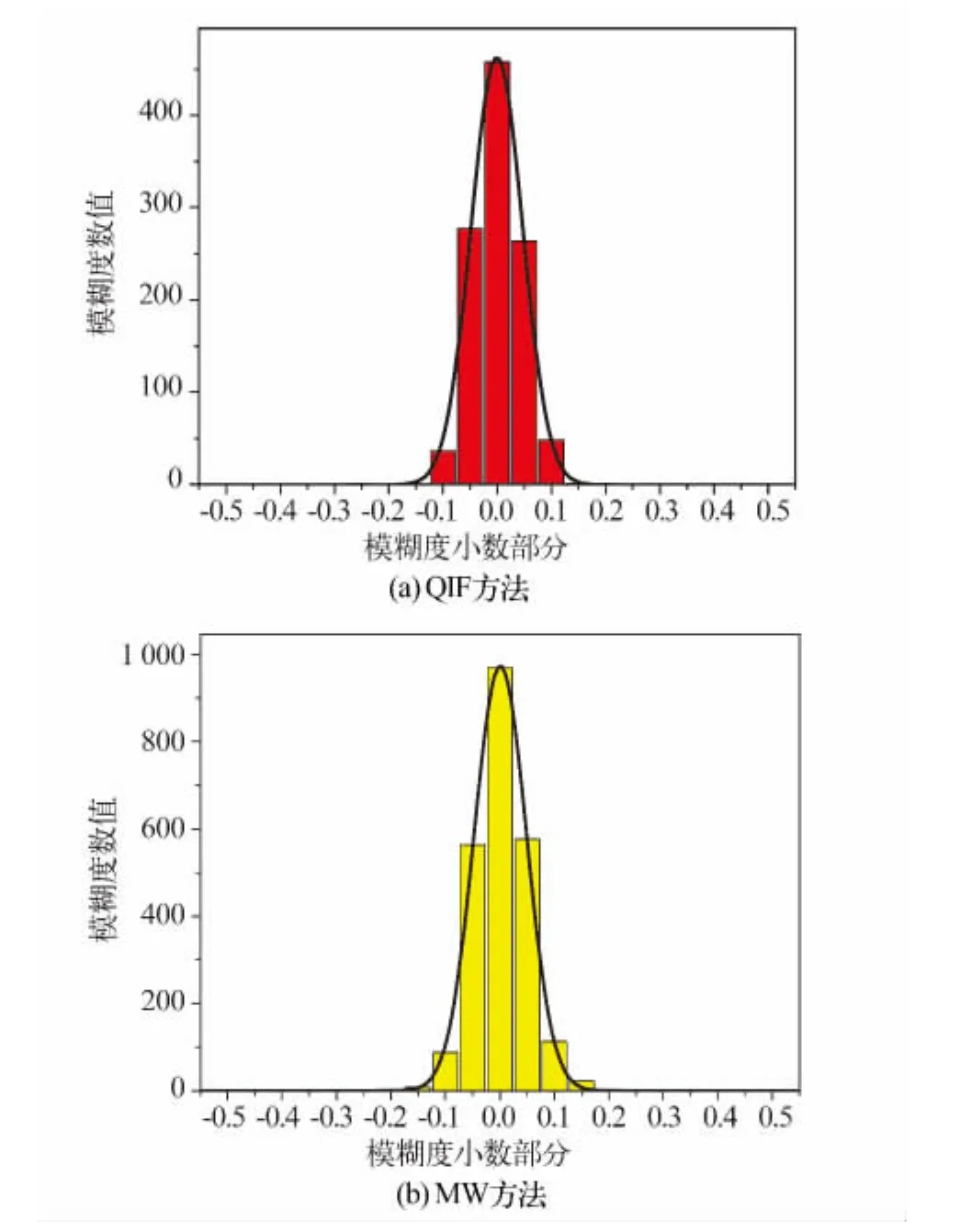
图3 KO_TM窄巷模糊度残差分布Fig.3 Distribution of narrow lane ambiguity residual of KO_TM

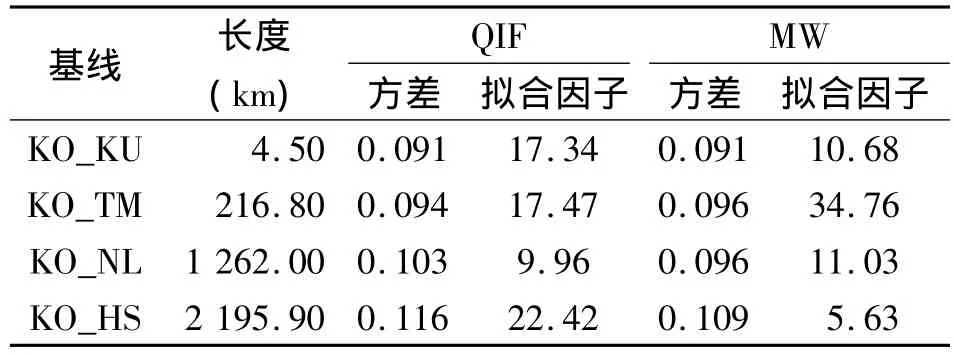
表2 各基线窄巷模糊度残差拟合因子Tab.2 Fitting factor of narrow lane ambiguity residual of each baseline

由不同长度基线窄巷模糊度固定残差的高斯拟合结果来看，对于短基线，QIF和MW拟合方差接近，随着基线长度的增加，两种方法得到拟合方差逐渐增大;对于超过2 000 km的长基线，MW拟合方差略小于QIF方法，主要原因是MW方法基本不受边长的限制。

5 个测站坐标重复性结果如表3和图6、7。

结果表明:用QIF方法和MW方法得到的五个测站的坐标水平方向重复性在2 mm以内，高程方向稍差，这与用GPS相对定位技术确定点位坐标精度特点相符合。测站NYAL和TROM坐标重复性较好，而KIRU测站在高程方向差异较大，说明对于短基线，两种方法计算效果不理想。

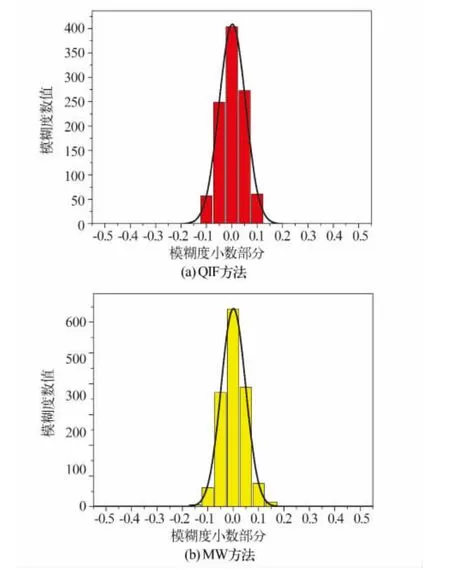
图4 KO_NL窄巷模糊度残差分布Fig.4 Distribution of narrow lane ambiguity residual of KO_NL

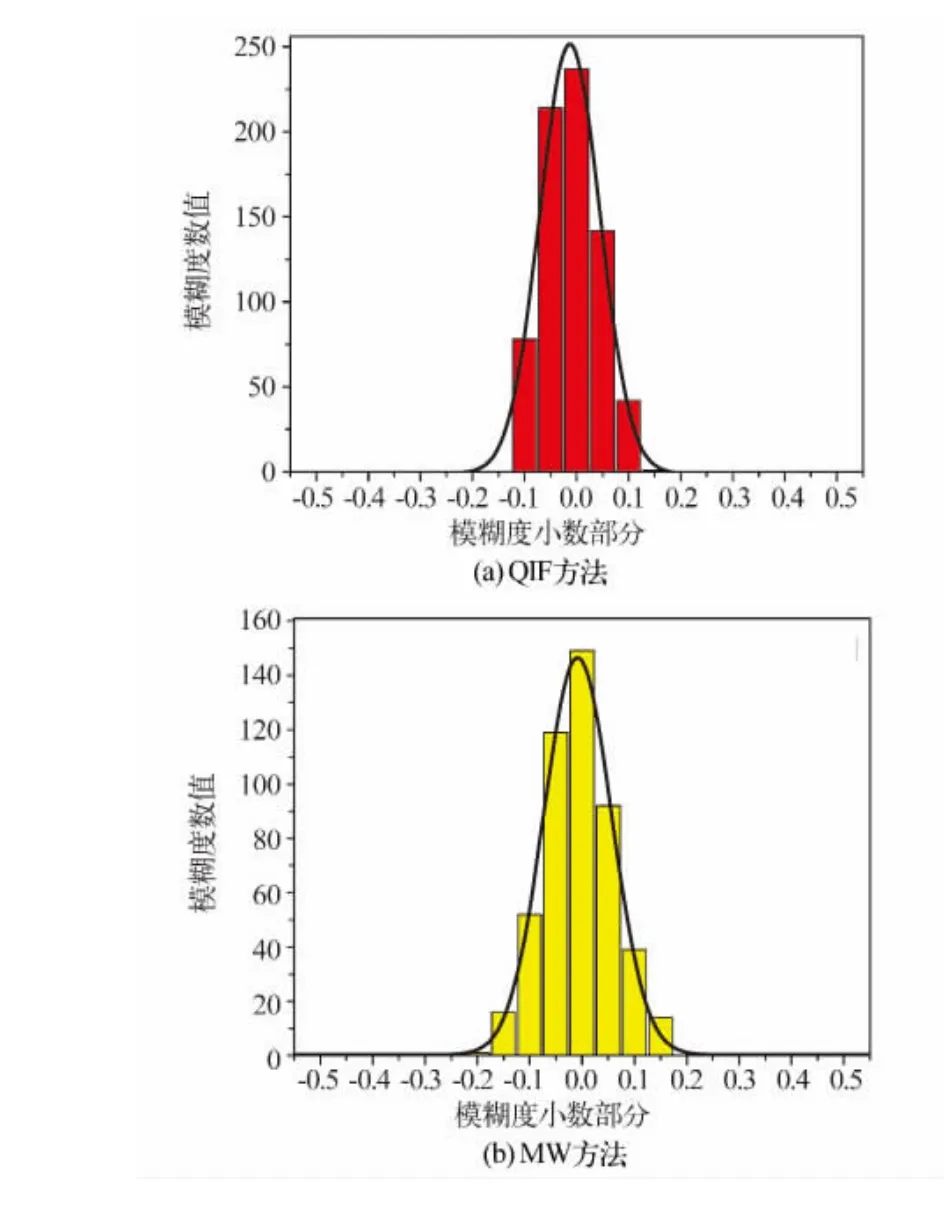
图5 KO_HS窄巷模糊度残差分布Fig.5 Distribution of narrow lane ambiguity residual of KO_HS

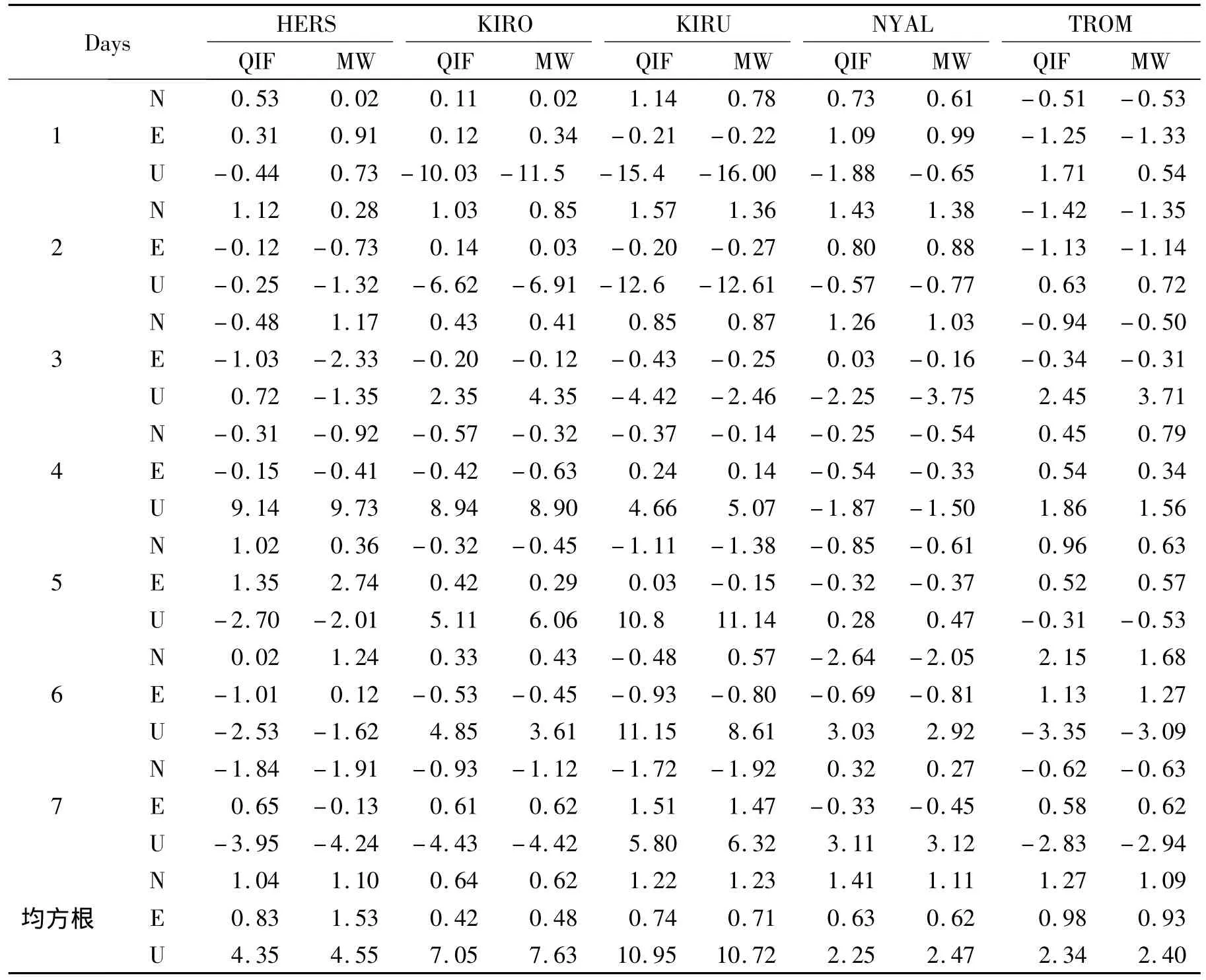
表3 各测站坐标重复性(单位:mm)Tab.3 Coordinate repetition of each station(unit:mm)

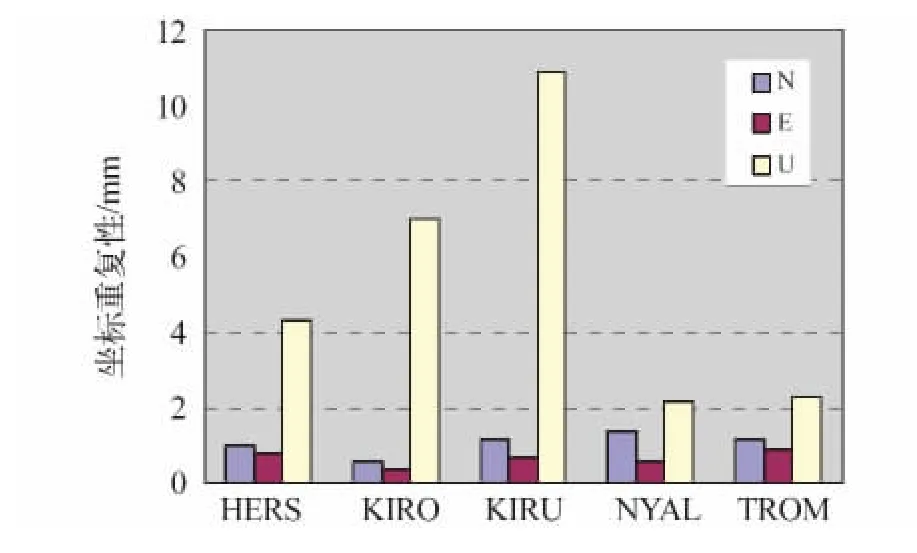
图6 QIF方法计算的各站坐标重复性Fig.6 Coordinate repetition of each station using QIF

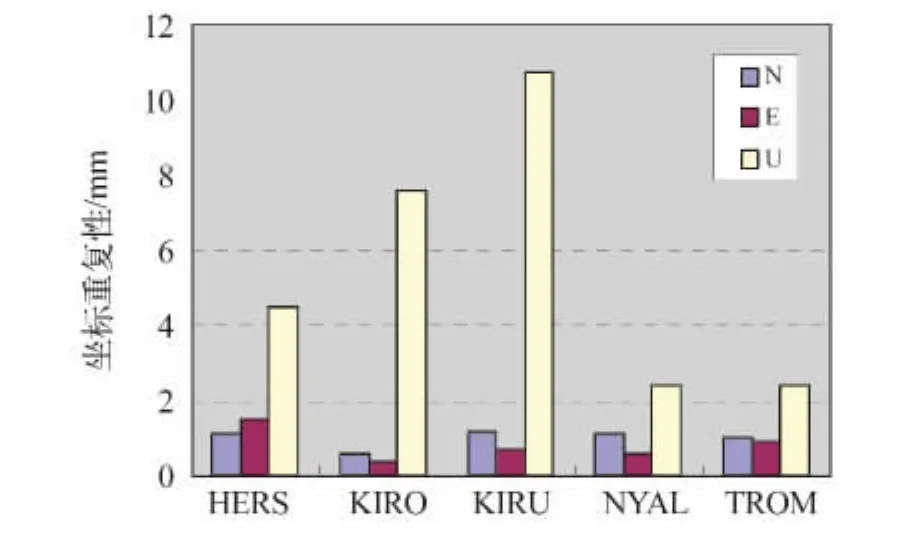
图7 MW方法计算的各站坐标重复性Fig.7 Coordinate repetition of each station using MW

6 结论

探讨了不同长度基线解算过程中模糊度分解方法的适应性问题，并引入了模糊度实数解与整数解之差的Gauss分布拟合方差、拟合因子和基线坐标重复性等物理量进行分析，结果表明:对于短基线，QIF和MW结果接近，均不理想，双差组合虽然能够很好地消除电离层等误差的影响，却增大了观测噪声，导致计算结果反而不好;对于超过2 000 km的长基线，MW略优于QIF方法，主要原因是MW方法基本不受边长的限制。

1 李博峰，沈云中，周泽波.中长基线三频GNSS模糊度的快速算法［J］.测绘学报，2009，38(4):296 －301.(Li Bofeng，Shen Yunzhong and Zhouzebo.A new method for medium and long range three frequency GNSS rapid ambiguity resolution［J］.Acta Geodaetica et Cartographica Sinica，2009，38(4):296－301)

2 魏子卿，葛茂荣.GPS相对定位的数学模型［M］.北京:测绘出版社，1998.(Wei Ziqing and Ge Maorong.The mathematical model of GPS relative positioning［M］.Bei Jing:Publishing House of Surveying and Mapping，1998)

3 Urs Hugentobler and Rolf Dach.Bernese GPS Software Version 5.0 DRAFT［M］.University of Bern，2006.

4 Blewitt Carrier.Phase ambiguity resolution for the global positioning system applied to geodetic baselines up to 2000 km［J］.Journal of Geophysical Research，94:

5 刘志平，等.GNSS模糊度降相关算法及其评价指标要求［J］.武汉大学学报(信息科学版)，2011，36(3):257 －261.(Liu Zhiping，et al.Decorrelation algorithms and it’s evaluation indexes for GNSS ambiguity solution［J］.Geomatics and Information Science of Wuhan University，2011，36(3):257－261)

6 Teunissen P J G.The probability distribution of the GPS baseline for a class of integer ambiguity estimators［J］.Journal of Geodesy，1999，73(5):275－284.

7 焦文海.地心大地坐标系与高程基准研究［D］.信息工程大学，2000.(Jiao Wenhai.A study of the geocentric geodetic coordinate system and vertical datum［D］.Information Engineering University，2000)

8 符养.中国大陆现今地壳形变与GPS坐标时间序列分析［D］.中国科学院上海天文台，2002.(Fu Yang.Presentday crustal deformation in china and GPS-derived coordinate time series analysis［D］.Shanghai Observatory，CAS，2002)

COMPARISON BETWEEN QIF AND MW FOR AMBIGUITY DECOMPOSITION

Zhou Wei1，2)，Feng Laiping3)，Wang Yongshou1)and Yao Feijuan1)
1)China Luoyang Electronic Equipment Test Center，Luoyang471003
2)College of Navigation and Aerospace Engineering，Information Engineering University，Zhengzhou450052
3)Xi’an Research Institute of Surveying and Mapping，Xi’an710054

Based on the QIF and MW methods，a large number of measured data formed different length baselines are calculated to analyze the applicability of the two methods for different length baselines.The results could provide a criterion to select the method of ambiguity decomposition.

ambiguity;QIF;Melbourne-Wübbena(MW);Gauss fitting;baselines

P207

A

1671-5942(2013)05-0086-05

2013-01-04

国家自然科学基金(41074020)

周巍，女，1981年生，博士，主要研究方向为GNSS理论与数据处理.E-mail:zhouwei_0611@163.com