顾及高程二次项的大地水准面与似大地水准面之差距*

徐新强 赵德军 楼 楠

(西安测绘总站，西安 710054)

顾及高程二次项的大地水准面与似大地水准面之差距*

徐新强 赵德军 楼 楠

(西安测绘总站，西安 710054)

用中国青藏高原某地区实测重力数据和SRTM3地形数据计算了该地区大地水准面与似大地水准面的差距。理论分析和数值计算表明，二者的差距与高程有很大的相关性，高程一次项在该地区的均值达到1.76 m，高程二次项的最大值达到0.03 m。

大地水准面;似大地水准面;空间异常;布格异常;SRTM3;C2项

1 引言

大地水准面具有明确的几何意义和物理意义，而似大地水准面有一定的人为因素，其几何与物理意义都不明确［1］。一般把大地水准面和似大地水准面的差距称为C2项改正［2］。C2项在低海拔地区一般达为分米级，但在喜马拉雅山可达3 m。现代确定大地水准面的方法是:首先由地面重力值按莫洛金斯基理论计算出似大地水准面，再加上C2项改正得到大地水准面。虽然我国采用相对似大地水准面的正常高系统，但本文对于认识二者的差异以及将境外高程基准统一到我国1985国家高程基准有一定的参考价值。

采用正高系统的国家，对C2项的研究比较深入［1－5］。国内学者在平面近似的条件下导出一个仅含高程二次项的封闭公式，经过模型检验发现与文献［2］相差很小［6，7］。本文将采用实测重力数据、SRTM3地形数据计算青藏高原某地区顾及高程二次项的C2项改正。

自主学习是学生在学习活动中自我决定、自我选择、自我调控、自我评价反思，发展自身主体性的过程。自主学习具有能动性，独立性和异步性三个基本特点。中职学生自主合作学习能力的培养具有重要意义。通过学生自主地分析、探索、实践等实现学习目标，从中不断提升自主学习能力成为一名真正社会所需的技能型人才。

2 计算方法

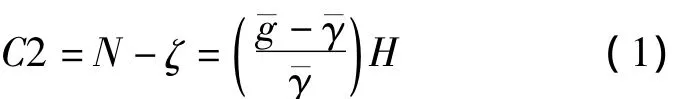
C2项用大地水准面高N和高程异常ζ之差表示，为［1］其中H是正高，¯γ是从地面沿正常力线到似大地水准面的平均正常重力，具有严密的理论值，但从地面沿力线到大地水准面的平均重力¯g很难获取。因此式(1)只能近似计算，文献［2］将其展开为正高的泰勒级数，顾及高程二次项的表达式为

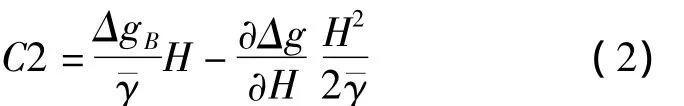
将右端第一项称为C21项，第二项称为C22项。Δg和ΔgB分别是空间异常和布格异常，ΔgB在陆地一般是负数，故通常似大地水准面在大地水准面之上。空间异常Δg经过地形改正和层间改正后就成了布格异常ΔgB，其中地形改正计算复杂且耗时，其平面近似条件下的计算式为［1］

其中B是计算点的大地纬度，γ是计算点投影到椭球面上的正常重力，f是椭球的几何扁率，m是克莱劳常量，a是椭球长半轴，本文采用GRS80椭球。空间异常垂直梯度的严密计算式为［1］:

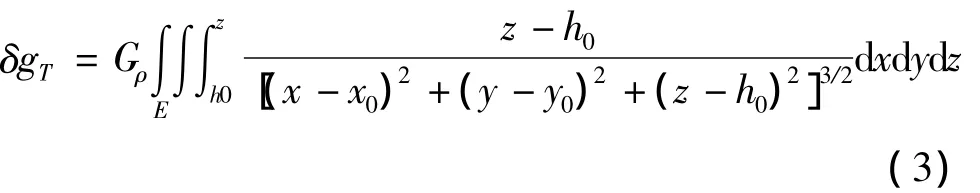
式中(x0，y0，h0)和(x，y，z)分别是计算点和流动点的坐标，G是引力常数，ρ为地壳密度，E是平面积分区域。计算式(3)有四棱柱法以及快速傅里叶法，许多文献给出了地形改正的改进算法并提供了相应的源代码［8－11］。本文使用 Fa2boug，因其除了具有地形改正功能外，计算层间改正时还顾及了地球的曲率，最终将 Δg转换为 ΔgB。¯γ 的计算为［1］:

(4)利用先进的科学技术使权力在阳光下运行。在相关制度中，可以作出这样的规定:除了涉及国家秘密的事务，其余一律必须予以公开。为此要加强研发和努力利用先进的信息技术手段，尽可能地使公共资源在网络上交易，政务在网络上公开，资金在网络上运行，监督在网络上实施。权力的运作如此公开、透明，就能使权力无从腐败。

在护理之前，两组患者的生活质量评分差异无统计学意义（P＞0.05），护理后，观察组优于对照组（P＜0.05）。见表2。

其中Δg0是计算点的空间异常，l是计算点到积分面元dσ的空间距离，R是地球平均半径。文献［1］认为，随着距离的增加迅速减小，积分计算主要集中在内区，将积分内区近似成平面，可写成:

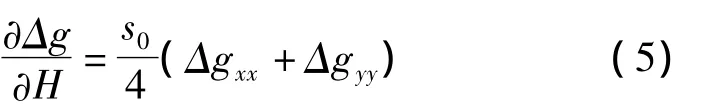
选取青藏高原北纬 33°～38°，东经 97°～102°的区域作数值实验。地形数据采用第4版3″×3″的SRTM3(图1)，其高程基准是EGM96定义的大地水准面，平面基准是WGS84，标称绝对高程精度是±16 m，绝对平面精度是±20 m［12］。此区域平均高程为3 892 m，最低高程1 999 m，最高高程6 194 m，标准差为587 m。并将SRTM3转换为分辨率为1'×1'和2'×2'的网格数据。空间异常采用实测的1'×1'平均空间异常(图2)，精度优于 5 ×10－5ms－2，其均值为 －7.4 ×10－5ms－2，最小值 －172.3 ×10－5ms－2，最大值 194.5 × 10－5ms－2，标准差为 44.7 × 10－5ms－2。

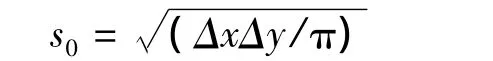
式中 Δx、Δy是网格间隔，Δgxx和 Δgyy分别是 Δg的水平二阶导数。

3 数值计算

其中s0是内区半径，

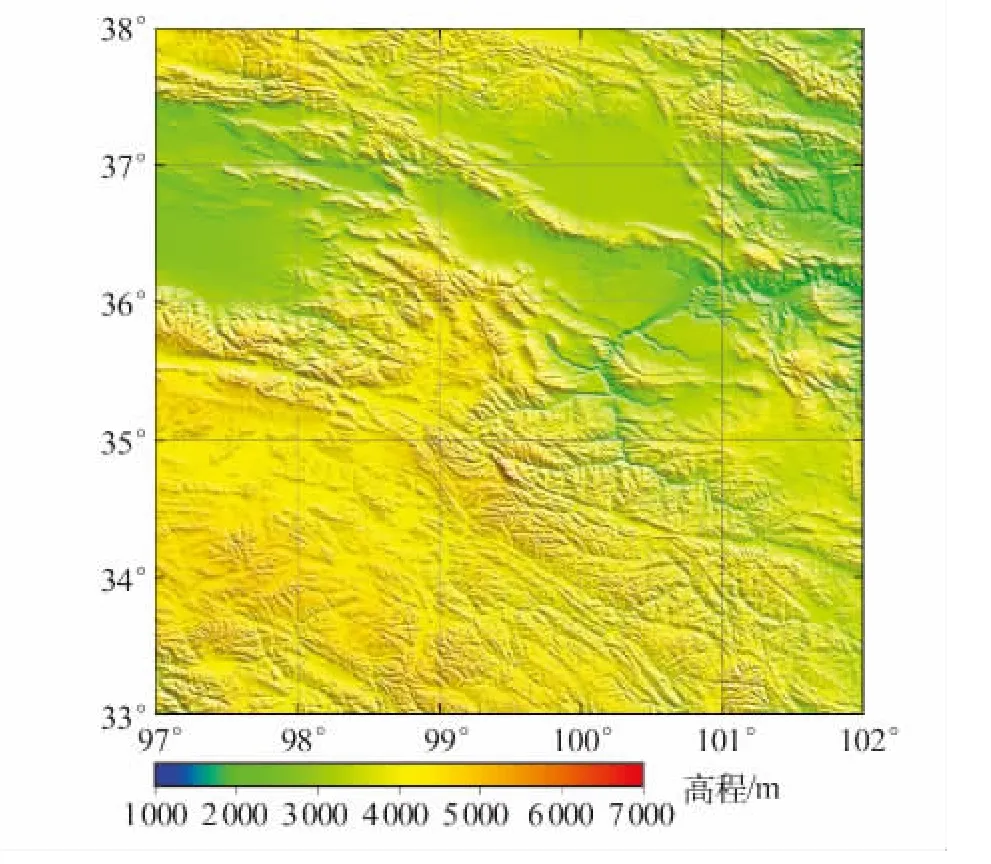
图1 SRTM3地形图Fig.1 SRTM3 topographic map

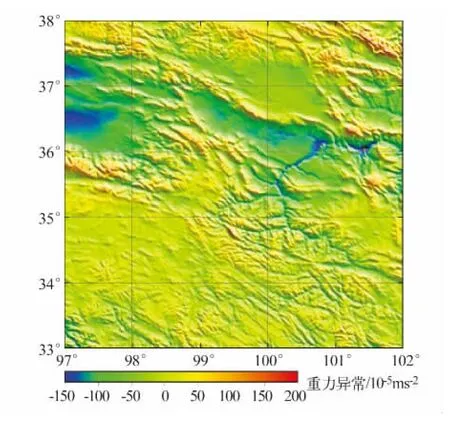
图2 空间重力异常Fig.2 Free air gravity anomalies

为了同时顾及计算精度和速度，将地形改正的积分半径分为3部分:积分内区采用3″×3″的DEM数据(积分半径为1')，中间区采用1'×1'的 DEM数据(积分半径为 1'～10')，远区采用 2'×2'的DEM数据(积分半径为10'～60')。地壳密度采用全球平均地壳密度2 670 kg/m3。

表1为计算结果统计。地形改正在本区域较小，是因为地形改正主要受地形起伏程度影响，与地面高程绝对大小无关，且地形改正在陆地为正。C21项在本地区较大，均值达到了1.76 m。相对于C21项，C22项较小，均值几乎为0 m，但某些地方绝对值也达到了0.03 m，因而在高精度计算中不能忽略。图3是布格异常渲染图，等高距为10×10－5ms－2，对比图2可看出，经过地形改正和层间改正后，相对较平滑。图4是C21项渲染图，等高距为0.5 m，对比图1可看出C21与地形高有某种相关性。为了证明此观点，将地形高与C2展点于图5(为方便显示只抽取了部分点)，从中可看出C2项与地形高有很高的相关性。

测算末级渠系水价应在严格控制管护人员、约束成本以及清理、取消不合理收费的基础上，按照补偿末级渠系运行管理和维护费用的原则核定，末级渠系水价的计算公式为：

表1 计算结果统计Tab.1 Statistics of output parameters

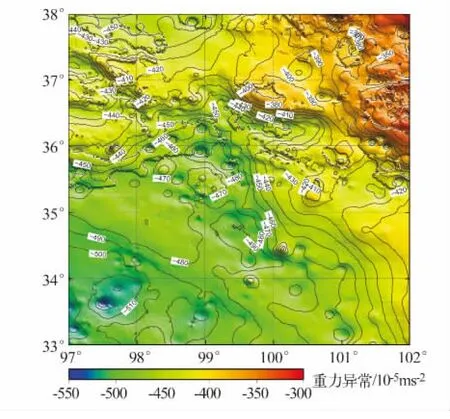
图3 布格异常Fig.3 Bouguer gravity anomolies

4 结论

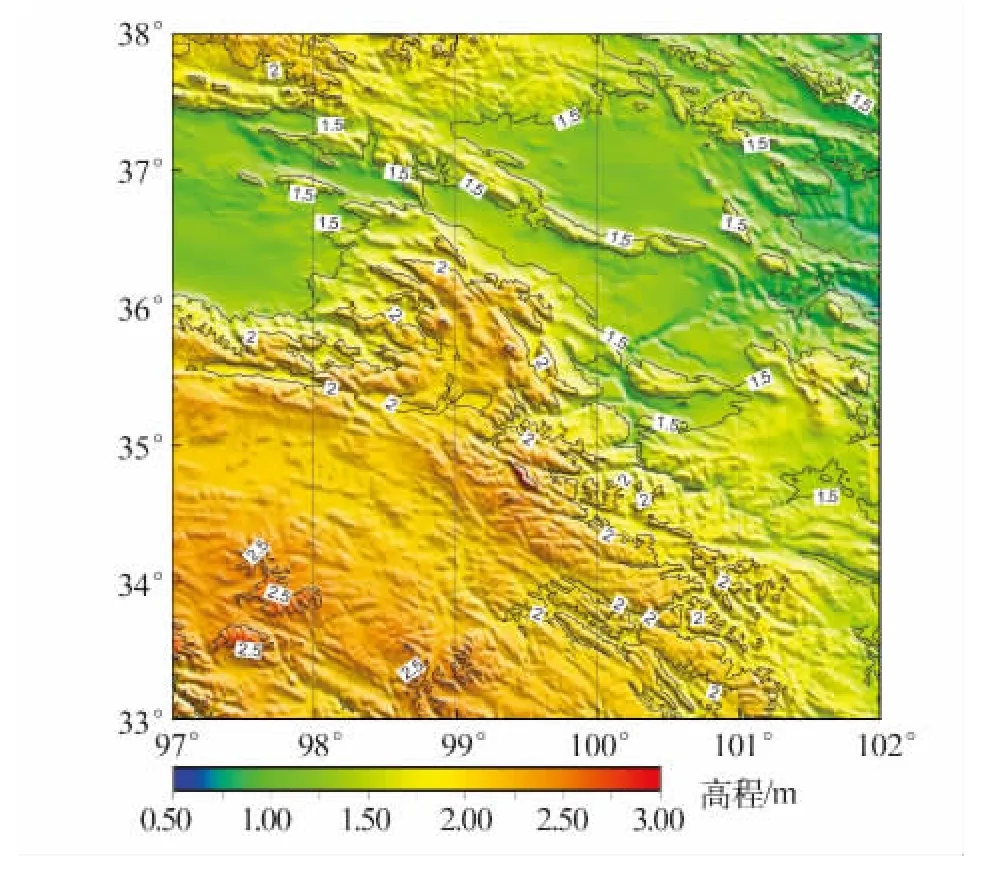
图4 C21项改正Fig.4 Correction of C21 term

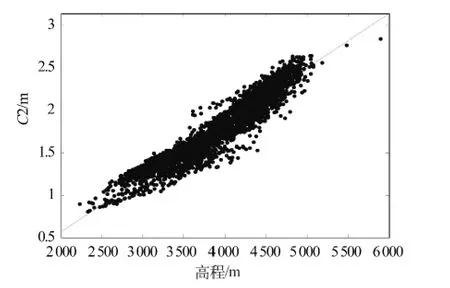
图5 C2项与高程的相关性Fig.5 Correlation coefficient between C2 term and elevation

本文给出了计算大地水准面与似大地水准面差距的详细计算方法，用实测空间异常和高分辨率地形数据，计算了顾及高程二次项的C2项。通过理论分析和数值计算可看出:C22项一般很小，不足C2项的1%，但部分地区能达到0.03 m，因此在高精度计算中不能忽略。C2项与高程有很大的相关性。布格异常的计算与地形起伏、地形高和地壳密度有关，因此在有条件情况下可以使用国际上发布的分辨率为2°×2°的7 层地壳密度模型 CRUST2.0［13］。

1 海斯卡涅W A，莫里兹H.(卢福康，胡国理译)物理大地测量学［M］.北京:测绘出版社，1979.(Heiskanen W A and Moritz H.Lu Fukang and Hu Guoli tran.Physical geodesy［M］.Beijing:Surveying and Mapping Press，1979)

2 Sj berg L E.On the quasigeoid to geoid separation［J］.Manuscr Geod.，1995，20:182 －192.

3 Featherstone W E and Kirby J F.Estimates of the separation between the geoid and the quasigeoid over Australia［J］.Geomatics Research Australasia，1998，68:79 －90.

4 Flury J and Rummel R.On the geoid-quasigeoid separation in mountain areas［J］.Journal of Geodesy，2009，83:829 －847.DOI:10.1007/s00190－009－0302－9.

5 Sjöberg L E.A strict formula for geoid－to－quasigeoid separation［J］.Journal of Geodesy，2010，84:699 － 702.DOI:10.1007/s00190－010－0407－1.

6 张赤军.论(N－ζ)公式的内涵及推求N的精度［J］.武汉大学学报(信息科学版)，2006，30(6):471－473.(Zhang Chijun.Content and precision determining of difference between geoid and quasigeoid［J］.Geomatics and Information Science of Wuhan University，2006，30(6):471－473)

7 张赤军，等.精化大地水准面的一种间接方法—异常及其梯度在其中的应用［J］.地球物理学进展，2009，24(1):75 －81.(Zhang Chijun，et al.An indirect method for refining geoid，and on application of gravity anomaly and gravity vertical gradient［J］.Progress in Geophysics，2009，24(1):75－81)

8 Banerjee P.Gravity measurements and terrain corrections using a digital terrain model in the NW Himalaya［J］.Computers ＆ Geosciences，1998，24:1 009 －1 020.

9 Biagi L，Sanso F.TcLight:A new technique for fast RTC computation［R］.IAG Symposia，Gravity，Geoid，and Geodynamics 2000.Berlin:Springer，2001.

10 Hwang C，et al.Terrain correction computation using Gaussian quadrature［J］.Computers ＆ Geosciences，2003，29:1 259－1 268.DOI:10.1016/j.cageo.2003.08.003.

11 Fullea J and Fernandez M.FA2BOUG－A FORTRAN 90 code to compute Bouguer gravity anomalies from gridded free－air anomalies:Application to the Atlantic－Mediterranean transition zone［J］.Computers ＆ Geosciences，2008，34:1 665－1 681.DOI:10.1016/j.cageo.2008.02.018.

12 陈俊勇.对SRTM3和GTOPO30地形数据质量的评估［J］.武汉大学学报(信息科学版)，2005，30(11):941 －944.(Chen Junyong.Quality evaluation of topographic data from SRTM3 and GTOPO30［J］.Geomatics and Information Science of Wuhan University，2005，30(11):941 －944)

13 胡敏章，李建成.顾及地壳密度模型的Airy－Heiskanen均衡重力异常的计算［J］.大地测量与地球动力学，2010，(5):48－52(Hu Minzhang and Li Jiancheng.Computation of Airy－Heiskanen isosatic gravity anomaly with considering crust density model［J］.Journal of Geodesy and Geodynamics，2010，(5):48 －52)

A GEOID TO QUASIGEOID SEPARATION CONSIDERING SECOND ORDER HEIGHT TERMS

Xu Xinqiang，Zhao Dejun and Lou Nan
(Xi’an Division of Surveying and Mapping，Xi’an710054)

The separation between geoid and quasigeoid by using observed gravity data and SRTM3 terrain data in some areas of Qinghai-Tibet plateau was determined.Theory analyses and numerical tests showed that there existed a high correlation between the separation and elevation，and the average correction about first order height terms could be up to 1.76 m，and the maximum correction about second order height terms could be up to 0.03 m.

geoid;quasigeoid;free air gravity anomalies;Bouguer gravity anomalies;SRTM3;C2 term

P223

A

1671-5942(2013)05-0075-04

2013-03-06

国家自然科学基金(41104047);大地测量与地球动力学重点实验室开放基金(SKLGED2013－4－5－E)

徐新强，1968年生，高级工程师，研究方向为大地测量数据处理及地球重力场.E－mail:xaxcq@126.com