具有迟滞效应的交通基本图模型及仿真
吴中,王梅妞
(河海大学 土木与交通学院,南京 210098)*
0 引言
道路交通流作为数学、物理、信息技术和交通工程的跨学科基础研究,在国内外取得了很多重要的研究成果.上世纪 50年代 Lighthill&Whitham[1]、Payne[2]等人提出交通流的运动学模型 和 动 力 学 模 型;其 后,Kühne[3]、Kerner-Konhaüser[4]以及我国学者张红军[5],薛郁[6]等人从不同角度加以改进,提出相应由偏微分方程描述的基于“流体”思想的交通流模型;此外,基于颗粒流理论和多智能体理论的交通流模型与仿真方法也得到了长足的发展.近年来,德国学者Kerner[7]等人通过现场实测发现 q-ρ关系图的数据分布不同于传统线性或非线性理论,提出了交通流的分相理论—三相交通流理论.三相交通流理论的提出冲击了传统理论,也对不断发展的运动学、动力学模型提出挑战,使得深入揭示交通流本质、提高模型精度成为现代交通流研究的重要方向之一.
1 Kerner与传统基本图的区别
在传统的交通流理论中,交通流量q和交通密度ρ的关系被表达成静态的确定关系,其二维关系图被称为基本图,具有物理意义明确、直观的特性,是表达交通流特征的重要方法.线性理论的图形曲线为二次抛物线,可由Greenshields速度与密度模型推导而得(图1).国内外根据交通流实测资料,将基本图表达成多种形态,接近于抛物线的曲线或折线.它们虽没有给出具体的数学表达式,但经验基本图具有曲(折)线连续、密度ρ对应单值流量q、流量存在确定的上限值、只有当密度为零或为阻塞密度时流量为零以及有包括正斜率自由流与负斜率拥挤流的特点.交通流的动力学方程以流体动量方程为基础,设想并描述了车流随体加速度随车流密度梯度、速度梯度或速度偏离值改变的车流状态变化特性.交通流动力学方程是人为构造的,没有严格的物理学基础,本质上只是流体运动的近似,即使确定了随体加速度,也难以直接给出固定空间位置的基本图关系.Kerner在基本图(图2)上将交通流分为畅行相(自由流F线)、宽幅运动阻塞相(J线)和同步交通流(二维阴影区),明确提出了存在高流量的亚稳定状态(大于qout的F曲线部分)和同步交通流,并依此可以解释“幽灵”阻塞现象和非畅行相条件下的交通流因加减速速度差引起的迟滞现象(图3),而迟滞(环)现象在传统基本图上几乎无法正确解释.
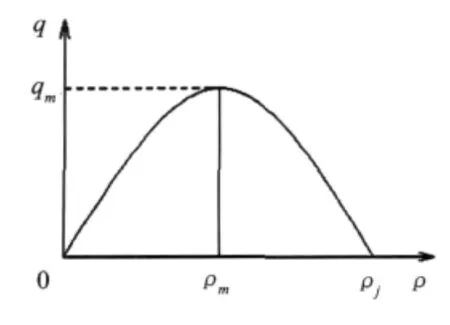
图1 Greenshields q-ρ基本图
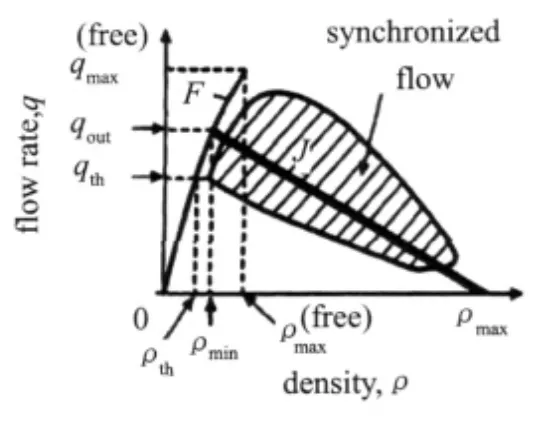
图2 Kerner交通流基本图
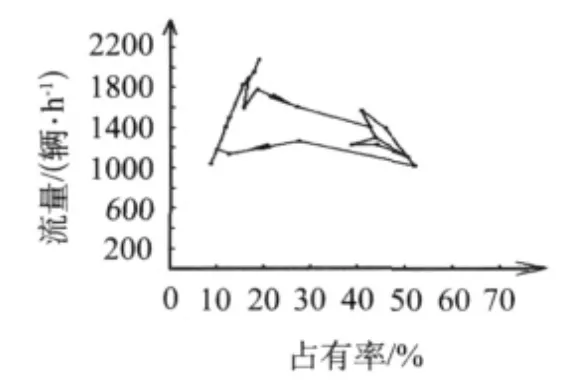
图3 [8]实测交通迟滞(环)
2 具有迟滞效应的基本图模型
2.1 模型构建原则
由于传统模型无法描述交通的同步流状态,其数值仿真也难以表达拥挤的交通流走走停停、忽快忽慢的特征;Kerner的q-ρ图因曲线不连续、同步流的q的多值特性,也不能够作为数值模型的控制方程.要在基本图控制模型或方程中表达拥挤车流的复杂特性对流量、流速的影响,需要结合上述两类基本图的特点,构造新的基本图模型.模型的构造遵循下列原则或假定:
(1)模型能够合理表达Kerner三相流理论的主要特性,包括同步流、交通迟滞(环);
(2)模型曲线连续,q-ρ关系变化规则明确,具有可计算性;
(3)考虑相同性质的单一车流,排除因车辆或驾驶行为差异而导致的最大流量值大小不定,即流量存在确定的最大值,仅当密度为零或阻塞密度时流量为零;
(4)模型引入合理边界条件,能够解释同步流与迟滞环现象的产生机理.
2.2 模型构建
依据上述原则或假定构建基本图(图4).图中具有正斜率的直线段为自由流,直线顶端对应最大交通流量,相当于Kerner基本图亚稳定状态交通流的最大值.由于只有在交通流内部车辆之间协同关系最理想时才能达到最大通过量(实际情况下较难达到),交通流量最大点只能出现在车流秩序最好的畅行相直线F顶端qm;同步流因交通秩序不如畅行相好,其最大流量、q-ρ二维包络线顶端值不可能大于畅行相qm值.畅行相直线顶端qm可依据大于等于实测同步流二维数据包络线顶端值确定.流量存在确定的最大值,畅行相直线顶端qm与阻塞密度之间的直线J可以认为宽幅运动阻塞相(图2、4).
在阻塞相直线J上下的区域为同步交通流,因车流中车辆拥挤程度与道路物理条件有关,同步流量的上下边界曲线1、2应依据极端的实测数据包络线或经验值确定(图5),同时也反映在速度-密度(V-ρ)平面的上下限曲线1、2(图6).
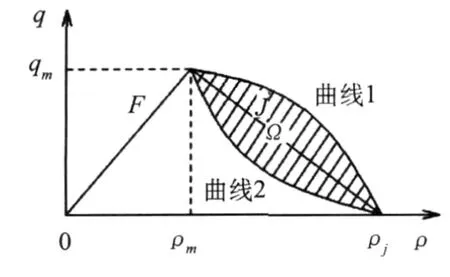
图4 新构建的具有迟滞效应的基本图

图5 具有迟滞效应的q-ρ图
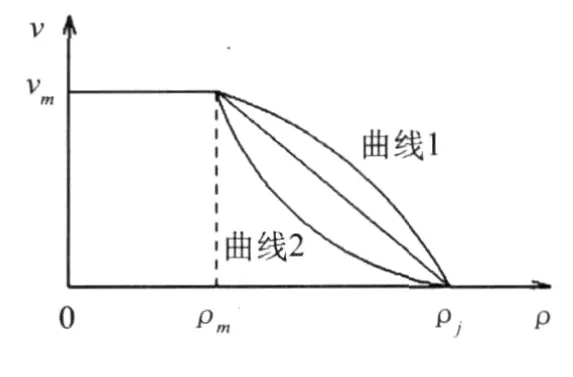
图6 具有迟滞效应的V-ρ图
模型认为均一车流的同步流q-ρ二维区域是由各种大小不等的动态迟滞环覆盖而形成.车流在拥挤区加速、减速会因加速动力一般弱于减速动力而产生加速的迟滞,即在V-ρ及q-ρ图上显示出加减速的不同车流状态路径.引入交通流任意状态点都可以达到极端状态的自然边界条件,每一时刻加减速状态变化路径按下列思想确定(图5):①在0~ρm区间内的车流状态变化沿F直线运动(式(1));②在ρm~ρj区间内的车流若要改变状态(加速或减速),车流状态改变必须沿着一条从当前状态点出发,加速能够达到ρm上限值、减速可达阻塞密度ρj下限值的V-ρ或q-ρ路径.车流状态由低速向高速变化,其V-ρ平面上的移动轨迹接近曲线2;状态由高速向低速变化,移动轨迹接近曲线1,在q-ρ平面上也是如此(图5、6).加速与减速的不同路径形成了迟滞环,迟滞环的速度曲线由Pipes-Munjal模型曲线族方程表达.尽管车流一时步状态改变并不一定能够达到上、下限值,但状态变化路径却必须满足自然边界条件,提供车流到达上下限值的可能,且状态变化路径方程并非不变,它是逐步逼近上下极值点(式(3)、(4));③为数值计算方便,当车流状态从畅行相进入阻塞相时(由0~ρm区间进入ρm~ρj区间),车流状态变化按阻塞相直线J选取q-ρ关系(式(2)).
构建模型可以表达为如下方程或计算式:
畅行相F:

阻塞相J:

宽幅运动相:状态变化路径是动态的.记n时刻交通流状态为 ρn,qn,下一时刻状态为 ρn+1,qn+1.若ρn+1>ρn,则车流量向阻塞状态靠近,其状态变化方程(路径)以当前的ρnvn为上限流量,以阻塞状态为下限,车流状态单时步变化方程为:
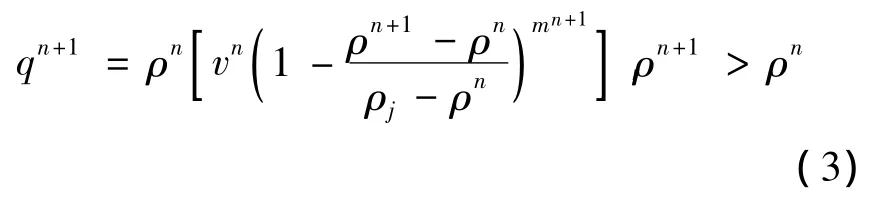
若ρn+1<ρn,则车流量向畅行相靠近,其状态变化方程(路径)以ρmvf为上限流量,以当前的ρnvn为下限,车流状态单时步变化方程为:
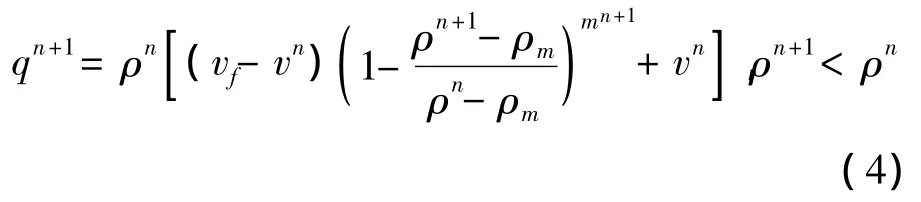
式(3)(4)中,因mn+1的取值不同,车流加速与减速的状态改变路径被区分(图5).若mn+1等于1,方程(3)、(4)退化为传统的折线基本图模型,既不存在同步流,也不存在迟滞环.此外,从式(3)、(4)中容易得到单时步车流速度变化方程.
表达偏离程度m值是时变的,以a、b为曲线1、2的极限指数值,0<β<1,为迟滞环路径改变速率参数,m变化规则可表达为:

式(5)中,a、b值可按调查数据取得或根据经验值选取.
3 数值模型与解法
3.1 数值模型
不添加扩散项,采用纯粹的车辆守恒方程为控制方程,交通流的“流动”的全部特性由方程或计算式(1)、(2)、(3)、(4)、(5)基本图模型表达,相应数学模型为:


其中,mn+1的取值见式(5).
3.2 数值解法
以下标i表示空间坐标,控制方程(6)在时间与空间上进行离散,采用Lax-Friedrichs格式,截断误差为时间一阶、空间二阶精度.离散方程可表达为式(8).

由于在ρm处q不可导,数值计算中多少会引起q数值结果的离散.符合Kerner观测数据在亚稳定状态qm处流量值离散与分裂的现象.
4 数值算例
模拟简单路段长8 km的单向两车道,模拟时间长2 200 s,空间步长10 m,时间步长0.1 s;畅行速度取80 km/h,阻塞密度取200 pcu/km,临界密度取50 pcu/km.车辆入流端为按时间步长给定的密度值,出流端为无反射开边界.使用sufer软件绘图,k表示密度、q表示流量、u表示速度;simulation time(s):仿真时间,section length(*10 m):仿真空间.
4.1 恒定密度输入
路段初始密度值为40 pcu/km,低于临界密度;入流源交通流密度波为恒定输入80 pcu/km,高于临界密度.由于高密度车流的输入,随时间推移,高密度车流将在空间上向前移动,密度波峰面处会发生扩散.
图7为没有迟滞环与同步流的退化模型的三参数计算结果,由于ρ和q一一对应(基本图仅由图5中F和J线构成),三参数计算曲面连续光滑,与其它成果一致.由于本文退化基本图模型在ρm处产生转折,计算密度与流量曲面上也有相应有曲面波动.由于Lax-Friedrichs格式有较强的频散性,加之时间步长很小,ρm处q不可导对计算结果的离散影响很小.

图7 三参数时空图(没有迟滞环与同步流)
考虑迟滞环与同步流,取a=0.8,b=1.6,迟滞环路径改变速率参数β=0.01,三参数计算结果见图8.与图7比较,密度、流量和速度随时间的变化趋势大体相同,车流在低密度畅行相区域三参数仍然曲面光滑.但在同步流区域三参数时空上变化更为剧烈,明显表现在流量与密度在空间上更大梯度的变化.由于迟滞环效应,高密度波向低密度扩教过程中产生车流速多次的快慢脉动(图8(c)).同时密度、流量图上也有起伏(图8(a)、图8(b)).
加大迟滞环效应,取a=0.8,b=2.0,三参数计算结果见图9.同步流区域三参数时空上梯度增大,由于扩散至低密度区的原高密度流车辆因迟滞环存在而减速,使得高密度波的扩散受到一时的阻碍,车辆被阻堵在最大流量密度ρm附近处,这种现象比图8更加明显,这也是输入恒定高密度车流引起的.此外,车辆加速减速幅度增加(图9(c)),也使在部分空间区域上密度在时间上时大时小,流量也有更大起伏,产生车流“走走停停”的现象.

图9 三参数时空图(加大迟滞环效应)
4.2 孤立密度波输入
路段初始密度值为40 pcu/km,入流交通流为40 pcu/km密度上的正弦孤立波,峰值60 pcu/km高于临界密度.图10为退化模型的三参数计算结果.密度在传播过程中逐步扩散、降低峰值(图10(a)),部分车流段密度的下降致使低速度“沟”逐渐收窄(图10(c)多峰形),曲面状态的改变缓慢光滑.

图10 三参数时空图(退化模型)
考虑迟滞环效应,取a=0.8,b=1.8,β=0.01,交通流孤立密度法输入不变,计算的三参数时空曲线见图11.与图10退化模型比较,密度波的扩散更快,密度与流量在空间分布上产生三个峰值(图11(a)、图11(b)),除了原先输入密度峰值外,输入密度波突然变化之处也会因密度的突然变化,使车流依据基本图与守恒方程产生加减速,并形成多峰形密度和流量的传递波.当密度发生较为剧烈变化时,迟滞环效应使得交通流行为更加复杂.

图11 三参数时空图(考虑迟滞环效应)
5 结论
研究结果表明,所建的包含迟滞环的均一车型交通流基本图模型,与传统的退化模型计算结果比较,计算三参数时空曲面发展趋势一致,细节上的差异能够合理解释,说明模型构建合理可信;时步流量变化模型描述了车辆中的迟滞环现象,同时也给出了同步流的合理解释,它是研究混合车型车流与不同驾驶行为车辆交通流的基础;算例比较表明,迟滞环是诱发车流降低稳定性的主要原因,加减速的不同路径会引起车流“走走停停”,甚至“幽灵”塞车的“罪魁祸首”.迟滞环效应越强烈,对稳定交通流的干扰就越大;依据包含迟滞环的交通流基本图模型,密度波因迟滞环而更快地扩散,这可能是交通密度波扩散速度大大快于扩散方程所描述的速度的原因;因为迟滞效应,在同步流相区间的交通流量很可能不同于退化模型所计算的流量,包含迟滞效应的交通流比传统交通流复杂很多.
真实的迟滞环现象很复杂,车辆、道路、驾驶人员因素都会影响到迟滞环的形成和迟滞路径,文中所提迟滞环是观测数据、合理假定与边界条件下的合理结果,仿真结果能够解释传统模型难以解释的交通现象,也能够解释三相交通流理论和现象.迟滞环研究还刚刚起步,探索交通流中的奥秘还需深入研究.
[1]LIGHTHILL M J,WHITHAM G B.On kinematic waves:Ⅱ.A theory of traffic flow on long crowded road[C].Proceedings of the Royal Society of London,1955:317-345.
[2]PAYNE H J.Models of freeway traffic and control:Mathematics models of public systems[J].Simulation Council Proceedings Series,1971,1(1):51-61.
[3]KÜHNE R D.Microscopic freeway model for dense traffic-stop-start waves and incident detection[C].Proceedings of the Ninth International Symposium on Transportation and Traffic Theory,1984:20-42.
[4]KEMER B S,KONHAUSER P.Structure and parameters of clusters in traffic flow[J].Physical Review E,1994,50(1):54-83.
[5]ZHANG H M.A non-equilibrium traffic flow model devoid of gas-like behavior[J].Transportation Research,Part B,Methodological,2002,36(5):275-290.
[6]薛郁.交通流的建模、数值模拟及其临界相变行为的研究[D].上海:上海大学,2002.
[7]KEMER B S.Introduction to Modern Traffic Flow Theory and Control[M].[s.n.]:[s.l.],2009.
[8]KEMER B S,REHBORN H.Experimental properties of complexity in traffic flow[J].Physical Review E,1996,53(5):21-25.

