不锈钢点焊地铁车车体结构稳定性分析
刘婷婷,刘海涛,陈秉智
(大连交通大学 交通运输工程学院,辽宁 大连 116028)*
0 引言
铁道车辆车体由车体底架、侧墙、端墙、车顶和司机室等几部分组成,一个合格的车体要能够承受垂向、横向、纵向和扭转等载荷.因此,在车体的结构设计阶段,车体除了要满足强度和刚度的要求外,还要对车体进行屈曲分析,以满足稳定性的要求.随着我国铁路八次大的提速和铁道机车车辆的轻量化进程的发展,铁道机车车辆的结构稳定性分析已成为铁路运输安全性的关键.
在结构力学研究领域,稳定性研究是最古老的问题之一[1].18世纪,欧拉就开始了对柱子稳定性的研究,同时基于小挠度理论提出了欧拉临界载荷;后来拉格朗日在此基础上对柱子的屈曲大变形理论进行了详细的研究,有利的促进了把稳定性分析理论成功的应用到铁道机车车辆行业[2].目前,我国铁道车辆的设计阶段在进行静强度和刚度分析的同时均进行车体稳定性分析,有时候也会出现一些问题,例如:车体侧墙变形过大、车体失稳等等.目前,我国对稳定性要求还没有相应的标准,株洲电力机车有限公司在企业内部的规范中明确规定:对所有具有车体进行屈曲稳定性计算,以保证车体在任何工况下都不会失稳[3].
本文以不锈钢点焊地铁车为载体,并对不锈钢点焊车车体结构的有限元模型进行了简单介绍.基于ANSYS软件,研究了点焊车车体在纵向压缩力为800 kN工况下的线性稳定特性.并比较了前后两种方案的分析结果.结果表明加密焊点可以增强侧墙的稳定性.并提出底架的修改意见,为不锈钢点焊车的生产和研发提供必要的理论依据[4].
1 车体稳定性分析
结构稳定性就是在外界干扰下,结构的自我控制能力.稳定性分析,又称为屈曲分析,包括计算分析载荷和解决失稳形状有关的问题两方面的内容.车体构件发生屈曲失稳的主要原因是作用在其上的广义膜应力引起的膜应变能转换成了弯曲应变能[5].对于一个受压的细长杆,当压力达到一定值的时候,一个很小的横向载荷就能产生很大的横向挠度,并且随着压力的增加横向挠度会急剧增大,从而导致杆件失稳[6].为了解决对结构稳定性的分析问题,基于有限元理论的数值分析方法应运而生,目前已在实际工程上得到广泛的应用[7].
2 算法原理
对于线弹性问题,在最小总势能原理的基础上,可以推导出基本的有限元平衡方程

式中,KE为结构的弹性刚度矩阵;D为位移向量;F 为外载荷向量[7].
在对结构的稳定性问题进行研究时,用几何矩阵Kσ来表示结构中的内应力对弯曲刚度的影响,所以式(1)可以表示成:
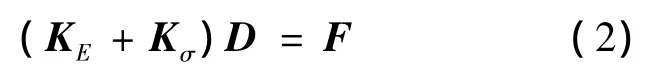
其中,Kσ的大小只取决于有限元的形状、单元的位移和应力分布.假设构件受力在线弹性范围内时,引入用来表示屈曲时的虚位移,那么有限元的平衡方程可转写为:

式中,λ为初始外力P0增加的倍数.当方程(3)有非零解时,λ就是该方程矩阵的特征值,与其对应的非零解向量为屈曲波形.

式中,Pcr为临界载荷;P0为初始外力.
有上面的公式可知:在KE已知的前提下,由应变方程出发,考虑到应变非线性项就可以推导出级和刚度矩阵Kσ.
式(4)表示的是广义特征值问题的屈曲方程,在求解工程问题的时候,用逆幂迭代法就可以求解出只关心的前几个特征值和特征向量.
3 车体有限元模型
本文利用HYPERMESH软件,基于真实的CAD图纸和三维几何模型建立不锈钢点焊地铁车的有限元模型.
建立点焊结构车体的有限元模型时,尽量多的考虑到对该车刚度及强度有贡献的结构,以尽最大可能地真实的反映出该车的实际情况.利用HYPERMESH软件,建立该车车体的几何模型和有限元模型.如图1、图2所示,其中,车体的几何模型的形状主要是从车体三维设计图中各构件的中面中提取出来;有限元模型是以任意四节点的等参薄壳单元为主,尽量减小模型中三节点薄壳单元的数量.与梁单元、板单元相比,等参薄壳单元综合考虑了构件中间面上的弯曲刚度、平面刚度和曲率效应,具有较高的计算精度[8].头车车体的有限元模型中单元总数:1 498 975,节点总数:1 418 019,其中梁单元:42 455个.图2给出了头车整车车体结构的有限元网格图.

图1 车体三维中面几何模型

图2 车体有限元模型
4 车体结构稳定性分析
4.1 评定标准、计算载荷及边界条件
依据计算要求,该点焊车车体结构稳定性安全系数为1.5.
对某不锈钢点焊结构TC车车体进行结构稳定性计算时,在车体一位端车钩坐处施加800 kN的纵向压力,在车体二位端车钩坐处施加纵向位移约束.
4.2 计算分析结果
4.2.1 初始设计方案的分析结果
初始设计方案的结构稳定性(线性屈曲)分析的屈曲因子λ较小的计算结果如表1所示,与其对应的屈曲振型如图3所示.

表1 初始设计方案的结构稳定性分析结果

图3 车体的屈曲振型
4.2.2 改进设计方案的分析结果
依据车体初始设计方案的结构稳定性分析结果,对车体结构的失稳部位:窗下纵梁区域的焊点进行了加密,形成车体改进设计方案.车体的结构稳定性(线性屈曲)分析中的较小屈曲因子λ的计算结果如表2所示,屈曲振型如图4所示.

表2 结构稳定性分析结果

图4 车体的屈曲振型
通过初始设计方案和改进设计方案结果对比可以发现加密侧墙蒙皮和窗下纵梁之间的焊点,车下纵梁再无发生屈曲,车体侧墙屈曲载荷显著提高,初始方案侧墙屈曲载荷是748.732 8 kN,改进后侧墙屈曲载荷是883.2 kN.因此在失稳区域增加焊点的密度,可以有效的提高车体的纵向刚度,进而增强车体受拉伸、压缩载荷时的稳定性.
5 结论
某不锈钢电焊车在承受车钩座处的800 kN的纵向载荷的作用下,对其进行结构稳定性分析的计算结果表明:
(1)临界载荷Pcr为883.2 kN(1.104×800 kN)时,侧墙蒙皮失稳;
(2)临界载荷Pcr为973.6 kN(1.217×800 kN)时,波纹地板失稳;
从以上结果中可以明显的看出车体的极限承载屈曲因子只有1.104,与1.5相差很多.因此该车失稳现象严重.
点焊车车体底架的地板和车体侧墙是一种薄壁结构,在拉伸、压缩工况载荷较易发生失稳,是车体最为薄弱的环节之一.为了改善车体受压状况,提高波纹地板区域的抗压能力,应调整底架横梁之间距离较大的位置,以增加波纹地板的垂向刚度,或在失稳区域增加纵向梁,增加车体的纵向刚度,是有效提高车体稳定性的一个途径.

图5 底架距离较大的横梁位置改进方案
建议:对底架距离较大的横梁的位置进行调整(改进措施参见图5);减少横梁之间的距离.或增加纵向梁.
[1]黄明高.轴重40 t矿石敞车车体结构非线性分析[D].长沙:中南大学,2007.
[2]王学文.铝型材地铁头车车体性能仿真关键技术研究[D].大连:大连交通大学,2007.
[3]岳译新,林文君,雷挺,等.地铁铝合金车体模态和稳定性有限元分析[J].机械,2008(4):20-22.
[4]韩强,张善元,杨桂通.结构静动力屈曲问题研究进展[J].力学进展,1998,28(3):349-360.
[5]马玉梅,付兴滨.大型落下孔车车体的结构分析及稳定性计算[J].应用科技,2004,31(7):13-15.
[6]单辉祖.材料力学教程[M].北京:国防工业出版社,1987:35-42.
[7]丁彦闯,兆文忠,马思群,等.屈曲分析在车辆应用中的关键技术[J].大连铁道学院学报,2003,24(2):44-47.
[8]郭乙木,陶伟明,庄茁.线形与非线性有限元及其应用[M].北京:机械工业出版社,2004:102-187.
[9]范国海,谢素明.车辆结构建模中的几个难点及对策[J].大连铁道学院学报,2000,21(3):8.

