铰接式轻轨客车车体结构强度的精细分析
谢素明,马巧艳,李娅娜,王剑
(大连交通大学 交通运输学院,辽宁 大连 116028)*
0 引言
铰接式车体结构形式、支承情况以及承载方式与非铰接式车体有很大区别,铰接式车体通过联接结构(以下称联接模块)来实现两车联挂并由转向架支承相邻车的端部.这类车体的联接和支承点位于缓冲梁外,其纵向力、横向力均要通过车体联接模块传至底架端部,故车体联接模块和底架端部受力大且结构复杂.然而,国内对这种类型车辆的研究主要集中在设计理论、组装工艺、通过性等方面[1-2].
为精细分析方案设计阶段的某出口铰接式轻轨客车铝合金车体结构的强度,首先创建了车体整体结构的一级薄壳单元有限元模型;在EN12663-2010标准[3]提供的静态载荷作用下,对整车结构进行了静强度分析;然后,在此基础上,基于子模型技术[4]构建了车体铰接部位接触非线性分析的二级有限元模型,分析与评价了铰接模块结构的强度.采用基于力学基本原理及大量焊接接头疲劳试验的计算焊缝疲劳寿命的主S-N曲线法[5-6],对铰接车体关键焊缝进行应力集中分析与疲劳寿命预测,并依靠焊缝的结构应力的分析,给出了提高焊缝疲劳寿命的改进设计方案.
1 铰接车体静强度精细分析方法
铰接式客车车体之间通过螺栓与联接模块相联.不难想象为较为准确地数值分析联接模块各部件(包括联接螺栓)而创建的铰接式车体的整体有限元模型的求解是具有相当难度且十分耗时.然而,利用子模型技术和接触非线性技术相结合的分析方法,即:在铰接车体的整体有限元模型(仅考虑螺栓传力)线性分析的基础上,采用子模型技术截取联接模块区域模型,重新对该区域(包括联接螺栓)采用实体单元进行有限元离散,并定义接触关系;然后,把原有模型在切割边界上的位移作为位移强制载荷施加到该区域模型的边界上,进行接触非线性分析.毫无疑问,这种分析方法可精确、快速地获得铰接式车体联接模块及联接螺栓的应力分布规律.
1.1 子模型法
子模型法是为获得位于整体模型中的部分区域中更加精细解的有限单元技术,又称为切割边界位移法(切割边界:就是子模型从整体较粗糙的模型分割开来的边界,整体模型切割边界的计算位移值即为子模型的边界条件).子模型法的理论基础是指定位移技术.
求解线弹性问题的有限元矩阵形式的方程为

式中,K为结构总刚度矩阵;D为结构待求位移向量;F为结构外载荷向量.假设D由D1和D2组成(其中D1为已知),则式(1)进行相应划分
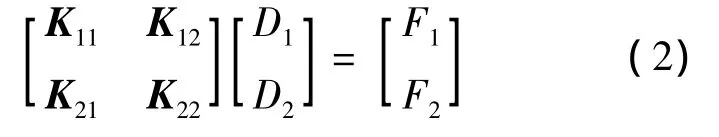
将上式展开,得
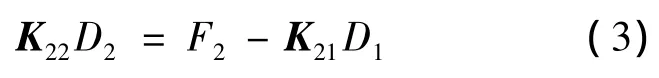
由式(3)可以看出:指定位移D1已经成为求解D2的载荷项的一部分.子模型技术就是利用式(3)实现的.
由于子模型边界条件取自较为粗糙的整体模型,即:子模型边界位移值需要插值计算才能得到.依据圣维南原理,如果作用在物体局部表面上的载荷被等效载荷代替,则离此区域较远部分所受影响才可以忽略不计.所以,子模型的边界应远离应力集中位置,这样子模型技术求解的区域才有可能得到较精确的结果.验证切割边界和应力集中位置的距离是否足够的方法是:通过比较子模型边界上的结果和整体模型相应位置的结果是否一致,若结果符合得较好,则证明边界选取是正确的;若不符合,则要重新定义离关心区域更远一点的切割边界.
1.2 接触非线性分析方法
两物体接触的有限元基本方程为
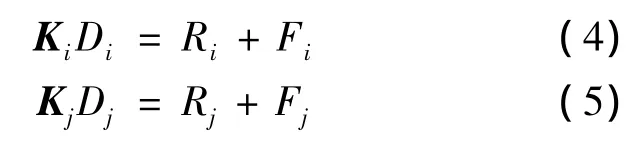
式中,Ki和Kj分别是物体i和j的刚度矩阵;Di和Dj分别是物体 i和 j位移向量;Ri和Rj分别是物体i和j的接触力向量;Fi和Fj分别是作用在物体i和j上的外载荷向量.由于两物体的位移向量和接触力向量均是未知量,所以,方程(4)和方程(5)不能直接求解.
在用有限元位移法求解接触问题时,首先假设初始接触状态形成系统刚度矩阵,求得位移和接触力后,根据接触条件不断修改接触状态,重新形成刚度矩阵求解,反复迭代直至收敛.由于接触关系会随载荷、材料、摩擦力、边界条件变化而变化,利用有限元方法进行接触非线性分析时,需要调整接触刚度、侵入参数以及确定接触算法和收敛准则等.进行包括螺栓在内的多体接触分析时,应先对螺栓进行预紧力工况分析,通过逐步调整上述参数、并随时调整接触有限元模型,使得结构在预紧力作用下达到一个合理的变形、均匀的应力分布,然后,再进行结构其它工况的静强度分析.
2 焊接接头应力集中分析与寿命预测方法
试验证明焊接接头对母材的屈服强度不敏感,其疲劳性能参数对屈服强度小于700 MPa的母材是一样的.在BS7608及IIW标准中,几何形状完全不同的焊接接头的S-N曲线是互相平行的,应力集中参数决定这些互相平行的曲线的高与低,大量的试验数据已经证明焊接方法对应力集中影响很小,主要是由几何不连续的差异所造成的.
美国ASME-2007标准中的主S-N曲线法是基于断裂力学理论及大量焊接试验,研究的一种相对准确计算焊缝疲劳寿命的新方法.为了有效地获得焊接接头焊缝上的应力集中参数,主S-N曲线法首先将焊缝上的应力分解成两部分:一是焊接工艺过程导致的非线性的自平衡应力,它与外力无关;二是由外力引起的,且与外力平衡的应力,即:结构应力.接着,基于有限元法,利用焊缝上的结点力一定与外力平衡的条件求其结构应力[7],该结构应力由两部分组成,一是弯曲应力,二是膜应力,于是,这个结构应力就给出了焊缝上的应力集中.通过对结构应力修正获得的等效结构应力,并将其作为S-N曲线参量,获得了分布狭小的S-N曲线试验数据,从而实现了以一条主SN曲线的模型[6]来预测焊缝的疲劳强度,很好地解决了当前设计阶段车体疲劳寿命评估方法遇到的焊接接头分类标准难以把握和焊接位置应力集中难以精确计算的两个难题[8].
由于焊接结构疲劳裂纹客观存在的特殊性,从力学机理上看,它的裂纹扩展过程仅是一个纯力学行为,与材料性能无关,因此,其疲劳寿命就可以用断裂力学的理论求解.其次,针对焊缝微裂纹的特点,将裂纹扩张分解为两个阶段,经过一系列推导[8],可以积分得到主S-N曲线法预测焊接结构焊缝疲劳寿命的计算公式为
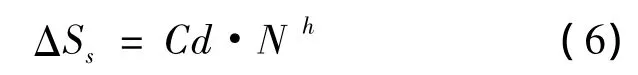
其中,等效结构应力的计算公式为

式(7)中的 Δσs为结构应力[9],反映了应力集中的影响;t反映了板厚度的影响,I(r)反映了载荷模式的影响;m=3.6,Cd及h为主S-N曲线试验常数,由ASME标准提供,N为疲劳寿命值.
3 铰接式车体的静强度分析
某出口轻轨编组列车由2辆带司机室的动车(MD)和2辆不带司机室的动车(M)组成;每辆车由A节和B节两节车体通过铰接模块连接组成,图1为编组列车的组成示意图.A节和B节车体的结构相同,但悬挂设备不同.车体地板、侧墙和车顶等均由铝型材焊接结构组成.
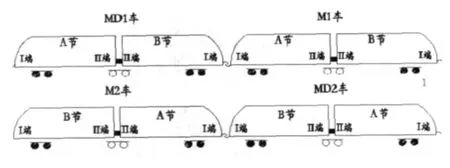
图1 出口轻轨编组列车组成示意图
为精细地分析车体联接部位各部件结构强度,首先建立铰接式车体整体结构的一级薄壳单元有限元模型(参见图2(a)),其中采用梁单元模拟联接螺栓的传力.在铰接式车体一级有限元模型分析的基础上,构建车体铰接部位的二级有限元模型(即:子模型),子模型中螺栓和与其连接的部件主要离散为六面体实体单元,其余部件采用薄壳单元;对螺栓和与其连接的部件定义接触关系,子模型的单元总数为419 515,节点总数为474 431.

图2 铰接式车体的有限元模型
在EN12663-2010标准提供的静态载荷作用下,对铰接式车体一级有限元模型进行静强度分析,计算结果表明:超载状态车体在车钩处承受500 kN的计算工况为恶劣危险工况,重点关注的部位应是受力大且结构较为复杂的铰接车体联接部位.在该工况作用下,铰接式车体的纵向位移如图3所示.

图3 车体的纵向位移云图
提取整车分析工况边界位移,施于子模型上,并对联接螺栓施加53.348 kN的预紧力.基于子模型技术,对车体联接部位多种设计方案进行接触非线性分析,最终方案的子模型位移如图4所示,其最大应力发生在联接螺栓上,数值为229 MPa(如图5),小于螺栓的许用应力.

图4 子模型的合成位移云图

图5 联接螺栓的Von.Mises应力云图
4 铰接式车体焊缝的抗疲劳设计
依据EN12663-2010标准,铰接式车体焊缝疲劳寿命预测的疲劳载荷工况为:①超载状态铰接车体垂向加速度a=1±0.15 g;②超载状态铰接车体横向加速度a=±0.15 g;③超载状态铰接车体纵向加速度a=±0.2 g.疲劳载荷循环次数为107.
预测铰接式车体焊缝疲劳寿命的有限元模型中应包含所评估焊缝细节在内.基于主S-N曲线法对车体焊缝抗疲劳设计的第一步是计算焊缝的焊址和焊根上的结构应力.具体地,根据车体在疲劳载荷工况作用下的有限元分析结果,提取焊线上的节点力,然后计算各焊线的结构应力及等效结构应力.最后,选用98%可靠度-2σ主S-N曲线(见附表)计算各焊缝的寿命次数.
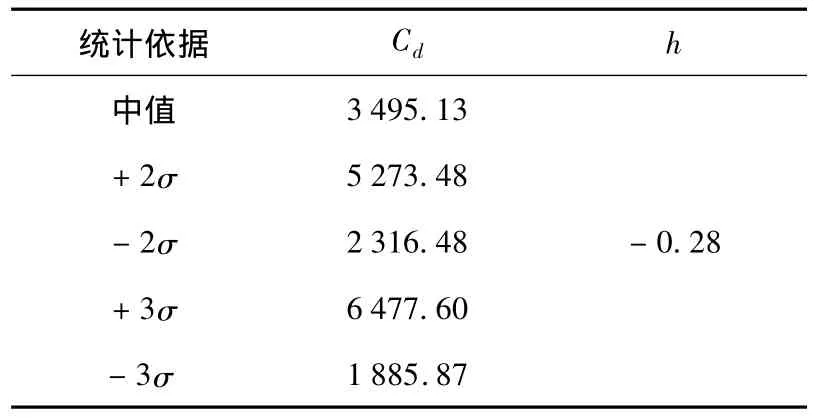
附表 主S-N曲线参数表

图6 车体焊缝疲劳寿命薄弱部位示意图
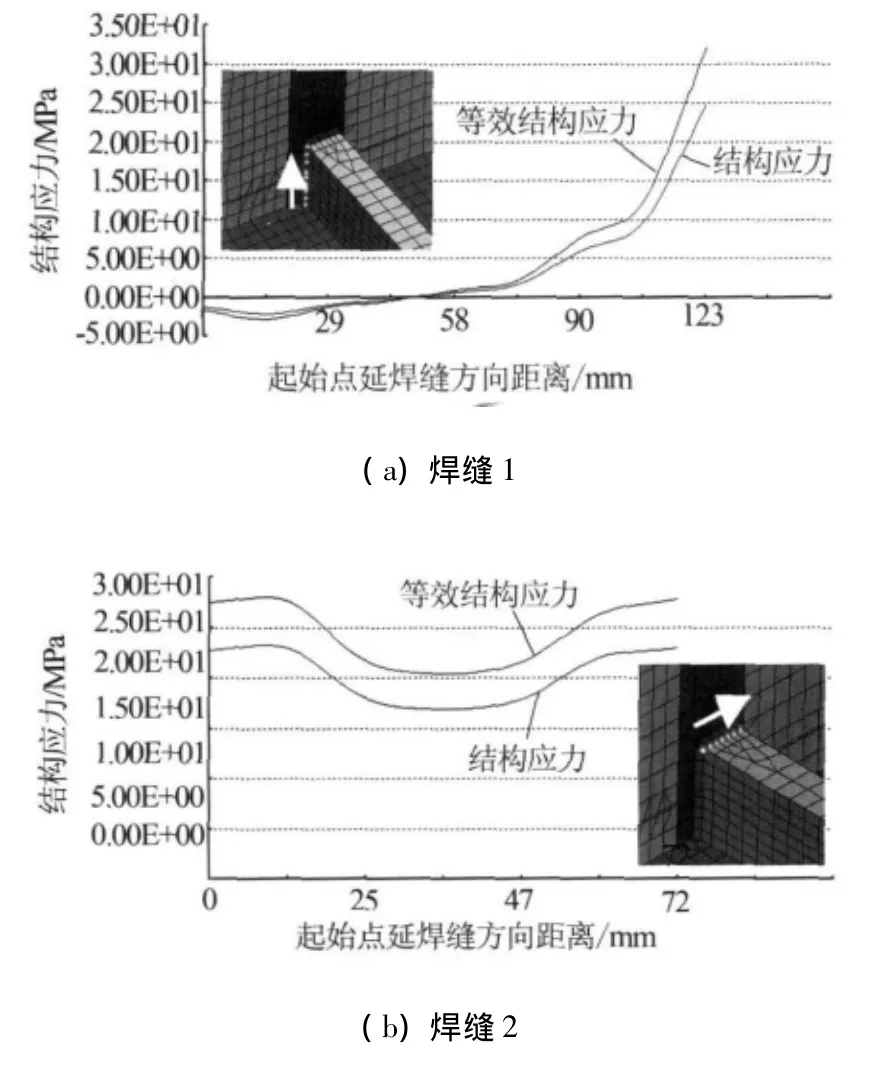
图7 焊缝结构应力随焊缝长度的变化曲线
在疲劳载荷工况1、2作用下,车体焊缝寿命次数均大于107;工况3作用下,车体焊缝疲劳寿命薄弱部位是车钩座与纵梁联接处(见图6),寿命次数在4.25×106与5.16×106之间.在工况3作用下,竖直焊缝1和水平焊缝2的结构应力沿着定义焊缝走向上的分布曲线见图7.图中白色箭头为焊缝方向;横坐标是从评估焊缝的焊线起点到焊线终点,其值与焊线上结点位置对应.
由图7可以看出:焊缝1的终点附近(即焊缝2的起点附近)的结构应力值远高于其它点的,也就是说在此处出现了应力集中,导致焊缝寿命低.为降低焊缝结构应力幅值,尽最大可能地协调该处的刚度,对车体车钩座处结构进行了改进设计,经多方案对比分析,最终设计方案如图8所示.

图8 车体焊缝结构改进示意图
改进设计方案的车钩座处焊接结构焊缝焊线I、II和III的结构应力沿着定义焊缝走向上的分布曲线见图9.对比分析图7和图9,车钩座与纵向梁相接处竖直焊缝的结构应力幅值减少了14 MPa,水平焊缝的结构应力幅值减少了6.8 MPa,应力集中得到了一定程度的缓解.改进设计方案的车钩座处焊缝的寿命次数均大于1.8×107.


图9 焊缝结构应力随焊缝长度的变化曲线
5 结论
基于车体一级薄壳单元和二级实体单元有限元模型,采用子模型与非线性接触分析相结合的方法,对铰接式轻轨客车铝合金车体静强度进行了精细分析,经接触非线性数值试验,优选出合理的铰接模块设计方案;基于主S-N曲线法,对车体焊缝进行了应力集中分析与疲劳寿命预测,指出了车钩座与纵向梁相接处是车体疲劳寿命的薄弱部位.改进设计方案的车钩座处焊缝寿命次数大于1.8×107.给出了满足EN12663-2010标准性能要求的铰接式车体的设计方案.
这种对铰接式车体静强度和焊缝疲劳寿命的分析技术完全可推广到其它复杂产品结构的性能仿真中.
[1]王欢,戴焕云,池茂儒.100%低地板轻轨车辆结构型式研究[J].内燃机车,2009,427(9):11-14.
[2]沈继强,卜继玲,黄运华.城轨列车铰接式转向架方案及其动力学性能研究[J].铁道机车车辆,2008,28(5):36-39.
[3]BSI.BS EN 12663-1:2010铁路车辆车体的结构要求(第一部分:机车和客运车辆)[S].英国:[s.1.],2010.
[4]周宇,万朝燕,谢素明.基于子模型的铁路车辆结构强度精细计算[J].铁道机车车辆,2009,29(1):16-18.
[5]ASME VIII.DIV2-2007 Boiler and Pressuire Vessel Code[S].美国:[s.1.],2007.
[6]Dong P,Prager M,Osage D.The design master S-N curve in ASME DIV 2 rewrite and its validations[J].Welding in the world,2007,51(5-6):53-63.
[7]DONG P,HONG J K.Analysis of Recent Fatigue Data Using the Structural Stress Procedure in ASME Div 2 Rewrite[J].Journal of Pressure Vessel Technology,2007,129:355-362.
[8]李晓峰,谢素明,时慧焯,等.车辆焊接结构疲劳寿命评估方法研究[J].中国铁道科学,2007,28(3):74-77.
[9]DONG P.A Structural stress definition and numerical implementation for fatigue analysis of welded joints[J].International journal of fatigue,2001,23(10):865-876.

