麻城黑山羊母羊体质量与体尺的回归分析

索效军，张 年，熊 琪，李晓锋，杨前平，陈明新

（湖北省农业科学院畜牧兽医研究所，武汉 430064）

麻城黑山羊是湖北省具有代表性的地方优良肉羊品种，素以毛色纯黑、繁殖力高、早熟和肉质好而著称[1]，具有很高的开发利用价值，为国家级地方优良品种，有关麻城黑山羊的研究自20世纪90年代初期开始出现，且多是关于饲养管理、生产性能、杂交改良、疫病防控等方面研究，而对于麻城黑山羊体质量与体尺的相关性分析、通径分析和回归方程的研究还未见报道，本研究通过对麻城黑山羊母羊的体质量与体尺进行相关、通径及回归分析，建立最优回归方程，旨在为麻城黑山羊的选育和提纯复壮提供参考。

1 材料与方法

1.1 材料

试验在武汉市江夏区湖北省农业科学院肉羊场进行，随机选择常规饲养条件下的18月龄麻城黑山羊母羊43只作为研究对象。

1.2 测定指标与方法

测定指标有体质量（Y，kg）、体高（X1，cm）、体斜长（X2，cm）、胸围（X3，cm） 和管围（X4，cm）。使用测杖、软尺、电子台秤按文献测定方法测定[2]，测定时间为早晨7:00～10:00，空腹。

1.3 逐步回归分析方法

建立最优回归方程的方法很多，常用的是逐步回归法（Stepwise）[3]，主要是对全部的自变量X1，X2，...，Xp，按其对依变量Y贡献的大小进行比较，并通过F检验法，选择偏回归平方和显著的变量进入回归方程，每一步只引入一个变量，同时建立一个偏回归方程。当一个变量被引入后，对原已引入回归方程的变量，逐个检验其的偏回归平方和。如果由于引入新的变量而使得已进入方程的变量变为不显著时，则及时从偏回归方程中剔除。在引入两个自变量以后，便开始考虑是否有需要剔除的变量，只有当回归方程中所有自变量对Y都有显著影响而不需要剔除时，再考虑从未选入方程的自变量中，挑选对Y有显著影响的新的变量进入方程。不论引入还是剔除一个变量都称为一步，不断重复这一过程，直至无法剔除已引入的变量，也无法再引入新的自变量时，逐步回归过程结束。

在多元线性回归方程中，若有1个或几个偏回归系数不显著时，说明其对应的自变量对依变量的作用不显著，或者说其在回归方程中不重要，此时应从回归方程中剔除1个不显著偏回归系数对应的自变量，重新建立多元线性回归方程，再对新方程作新的显著性检验，直至多元线性回归方程显著，且各个偏回归系数都显著为止，此 时的多元线性回归方程即为最优多元线性回归方程[4]。

1.4 数据处理

运用SPSS 19.0软件进行体质量与体尺的相关、通径及回归分析，利用逐步回归方法建立体质量对体尺的最优回归模型[5-6]。

2 结果与分析

2.1 体质量与体尺性状的基本统计量

由表1可知，麻城黑山羊体高、体斜长、胸围（C.V＜10%）为弱变异，体质量、管围为中等变异（10%＜CV＜100%），其中体质量的变异幅度较大。

2.2 体质量与体尺性状的相关性分析

由表2可知，体质量与体尺性状存在极显著的正相关，其中胸围与体质量的相关程度最高（r=0.8380），其次是体斜长、管围（r=0.8354和r=0.7936）；各体尺性状间亦呈较强正相关，其中体高与体斜长的相关系数最大（r=0.7769）。

2.3 体质量与体尺性状的通径分析

体质量与体尺性状间的相关系数仅能反映表型相关，而通径分析可以显示指标间的直接、间接作用程度，根据相关系数的组成效应，可将麻城黑山羊母羊各体尺性状（Xi）与体质量（Y）的相关系数（rij）剖分为体尺对体质量的直接作用（Pi）和某一体尺性状通过其他体尺性状（Xj）对体质量的间接作用（∑rijPj）两部分[7-9]，即rij=Pi+∑rijPj，由表3可知，胸围对体质量的直接影响作用最大为0.4142，而体斜长对体质量的间接作用最大为0.5642。

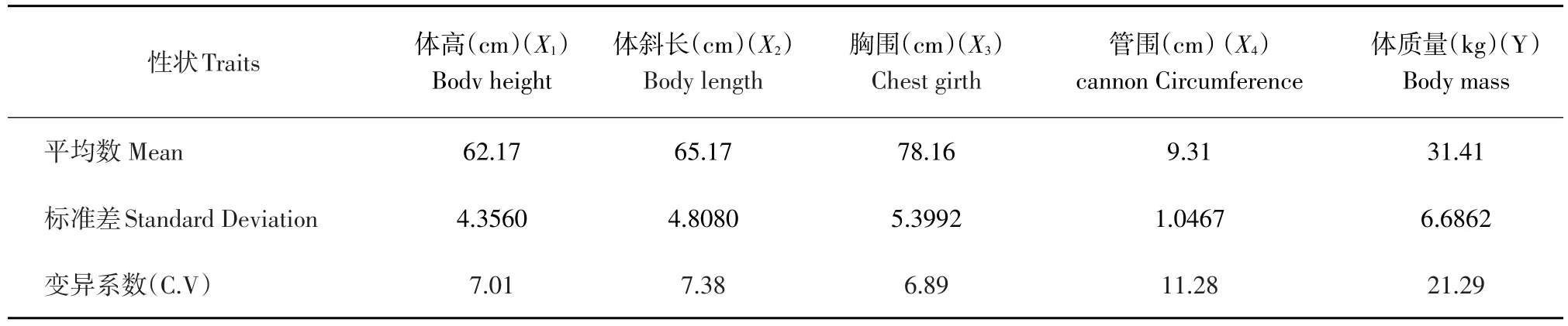
表1 体质量与体尺性状的平均数、标准差及变异系数Table1 Body mass and body measurement trait of the mean,standard deviation and coefficient

表2 体质量与体尺性状的相关性分析Table2 Correlation analysis of body mass and body measurements traits

表3 简单相关系数的分解Table3 Decomposition of simple correlation coefficient

2.4 最优回归方程的建立

2.4.1 自变量被引入回归方程后拟合优度的变化

回归方程1引入的自变量是X3，方程2引入的自变量是X3、X2，方程3引入的自变量是X3、X2、X4，从表4可知，自变量X3、X2、X4依次被引入回归方程后，其R值逐渐变大，估计标准误逐渐变小，如X3被引入回归方程时，其R值为0.8380，估计标准误为3.6922，当X2、X4依次被引入方程时，R值分别为0.9151和0.9417，而估计标准误分别为2.7617和2.3341。

表4 自变量被引入回归方程后拟合优度的变化Table4 The change of the goodness of fit after independent variables were introduced to the regression equation

2.4.2 方差分析

由表5可知，自变量X3引入回归方程后，其偏回归系数的F=96.7309（P＜0.0001）；自变量X3、X2引入回归方程后，其偏回归系数的F=103.0894（P＜0.0001）；自变量X3、X2、X4引入回归方程后，其偏回归系数的F=101.8860（P＜0.0001），而X1的偏回归系数无统计学意义，即对回归方程的影响不大，故未被引入回归方程。

2.4.3 偏回归系数及其T检验

各步引入对回归方程影响最大的变量时有关的偏回归系数及t检验结果见表6，引入X3时所得方程为Y1=1.0378X3-49.7110；引入X3、X2时所得方程为 Y2=0.6903X2+0.6248X3-62.4201；引入 X3、X2、X4变量所得方程为Y3=0.5120X2+0.4947X3+1.9679X4-58.9607，自变量X2、X3、X4所对应的P值均小于0.01。没有引入方程的X1在回归方程中其P值均大于0.05，无显著统计学意义，故为不重要变量。

综上所述，可认为逐步回归方程Y3=0.5120X2+0.4947X3+1.9679X4-58.9607是最优回归方程。

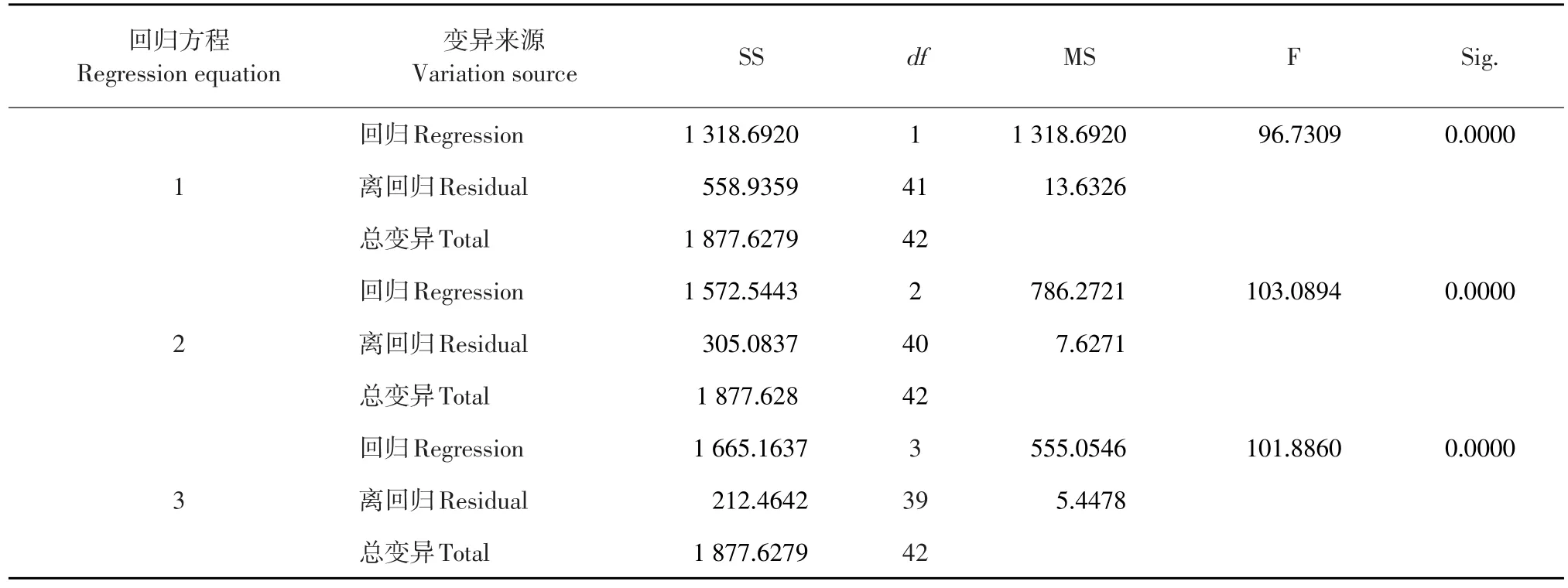
表5 回归方程的方差分析Table5 Analysis of variance of the regression equation

表6 体质量与体尺的多元回归分析Table6 Multiple regression analysis of body mass and body measurements traits

3 讨论与结论

3.1 体质量与体尺的变异系数

体质量与体尺性状是动物选育中重要的表型性状，与生产性能有密切关系。所测定的各性状表型参数变异系数较大，说明麻城黑山羊母羊在体质量、体尺性状方面具有较大的选育潜力。

3.2 体质量与体尺性状间的相关关系

麻城黑山羊的体尺性状与体质量有极显著的相关关系（P＜0.01），线性回归分析得出体斜长、胸围和管围每增加1 cm，体质量将分别增加0.5120、0.4947和1.9679 kg，说明这3个体尺指标对麻城黑山羊体质量增长方面影响较大。由相关系数分析可知，胸围对体质量的影响最大（r=0.8380），其次是体斜长、管围（r=0.8354和r=0.7936），体高的影响最小（r=0.6789）。体质量与胸围之间的相关是由于体质量与动物的肌肉、骨骼、内脏的生长发育紧密相关，同时体质量与体斜长、管围之间的相关是由于体质量与动物的肌肉、骨骼生长发育密不可分。因此，今后在麻城黑山羊的品种选育、提高生产性能等研究中，应以胸围为主并兼顾体斜长、管围，以取得较好的选育效果。

3.3 最优回归方程的建立

根据资料建立以体质量为依变量、体尺为自变量的回归方程：Y=0.5120X2+0.4947X3+1.9679X4-58.9607，最终入选回归方程的主要体尺性状有体斜长（X2）、胸围（X3）和管围（X4），拟合优度的决定系数（R2）值为0.8868，校正R2值为0.8781，回归关系都达到显著水平（P＜0.001），说明该回归方程已包含计算麻城黑山羊母羊体质量的主要体尺因素，表明应用该回归方程能够较准确地评估体质量变化。本研究中胸围、体斜长是影响体质量的主要因素，这一结果与陈碧红等[8]，高志英等[]的研究结果相吻合，但在回归方程中未选入体高性状，这可能与麻城黑山羊品种和测定样本数量小有关，入选的3个自变量简单易测，最优回归方程是一个准确、简便、适用的回归方程。

综上所述，体斜长、胸围和管围是影响麻城黑山羊母 羊体质量的主要因素，麻城黑山羊母羊体尺—体质量最优回归方程为Y=0.5120X2+0.4947X3+1.9679X4-58.9607。

[1]丁山河,陈红颂.湖北省家畜家禽品种志[M].武汉:湖北科学技术出版社,2004.

[2]陈伟生，徐桂芳.中国家畜地方品种资源图谱（下）[M].北京:中国农业出版社,2004.

[3]王欣荣,吴建平,杨联,等.甘南草地型藏羊体质量与体尺指标的相关性研究[J].甘肃农业大学学报,2011,46(5):7-11.

[4]王高富,黄勇富,罗艺,等.重庆黑山羊体尺和体重与胴体净肉率的回归分析[J].中国畜牧杂志，2009,45(21):9-12.

[5]苏理云,陈彩霞,高红霞.SPSS 19统计分析基础与案例应用教程[M].北京:北京希望电子出版社,2012.

[6]明道绪.生物统计附试验设计[M].北京:中国农业出版社,2002.

[7]杨佩燕,杨姣,刘志学.崇明白山羊和徐淮山羊体重与体尺的相关和通径分析[J].上海农业学报,2010,26(1):24-27.

[8]陈碧红,刘庆华.戴云山羊体尺与体重的回归分析[J].中国草食动物,2011,31(5):34-36.

[9]蔡惠芬,陈志,罗卫星.黔北麻羊体尺与体重的相关分析[J].畜牧与兽医,2012,44(7):53-55.

[10]高志英,乌云毕力克,艾尔肯江.德国美利奴成年母羊体尺与体重相关回归分析[J].草食家畜,2012,157(4):31-36.