Matlab在麦克斯韦速率分布律中的应用

蔡莉莉，张 琳

（华北科技学院，河北 廊坊 065201）

Matlab是一套高性能的数值计算和可视化软件，具有强大的数值、符号计算及绘图、动画功能，能形象生动、准确和科学地反映物理学问题［1－2］，而且该软件编程处理方便，效果形象直观。麦克斯韦速率分布函数是大学物理热学教学中很重要的一部分内容，是研究气体分子热运动、气体分子碰撞、大量分子热运动服从统计规律性等问题的重要理论依据［3］。由于这部分内容的数学知识涉及概率、积分等复杂公式，其理论抽象、计算量大、曲线难画，而 Matlab在数学推导、计算、绘图上有其独特的优势［4］，所以将Matlab软件的绘图和计算能力用于麦克斯韦速率分布函数的教学和研究中，通过Matlab形象地反映出复杂的物理函数式的含义及变化规律。在教学上更能生动和形象地以可视化形式展现热运动现象的图像，使需经过复杂的理论学习、抽象的思维理解才能认识的现象，简单而直观地呈现在学生眼前，帮助学生更深刻地理解和掌握麦克斯韦速率分布曲线的物理含义［5］。

1 麦克斯韦速度分布函数曲线

麦克斯韦认为：在任何方向，在单位速度间隔v～v＋dv内的分子数dN与总分子数N0的比值的分布规律为［6］

其中，k是波尔兹曼常数是热力学温度；m是分子的质量；v是某方向的速度，F（v）就称为麦克斯韦速度分布函数。对该函数用Matlab编程，以文件maxwellsd.m为名存盘，得到同种气体（以氧气为例）在不同温度下的F（v）～v曲线图，编程语句如下：

当分子的质量一定时，温度是参数，麦克斯韦速度分布函数的曲线形状由温度决定［7］，图1是氧气分子在不同温度下的麦克斯韦速度分布曲线，从图中可见不论温度如何，分布函数的曲线都是对称的，这说明在相等的速度间隔内，运动速度方向相反的分子数是同样多的，因而分子的平均速度为零，证实了热运动中气体分子沿各个方向运动的机会均等［8］。另外在F（v）～v曲线中间有一个峰值，这说明在速度接近零的速度间隔内，分子数比较多，而速度很大的分子比较少，而且温度升高峰值降低，而峰宽相应增加，表明在相同的速度间隔内，随着温度的升高速度小的分子减少了，速度大的分子增加了，说明温度越高分子运动越剧烈。

图1 不同温度下麦克斯韦速度分布曲线

2 温度、分子质量对麦克斯韦速率分布的影响

当只考虑速度的大小而不考虑速度的方向时，速度分布律蜕化为速率分布律。在三维速度空间中，在速度间隔vx～vx＋dvx，vy～vy＋dvy，vz～vz＋dvz内，分子数占总分子数的比例为［9］

引入速度空间的球坐标v，θ，φ以球坐标的体积元v2sinθdvdθdφ代替直角坐标空间的体积元dvxdvydvz，并对方位角φ从0到2π积分，对仰角θ积分，体积元变为4πv2dv，（2）式可改

写为

令

（3）式就是麦克斯韦速率分布函数，以温度为参数对（3）式进行编程，编程语句只需将文件maxwellsd.m中的速度分布函数改为速率分布函数，将速率分布范围设置为（0～1 600）m以文件maxwellsl.m为名存盘，运行该程序后得到不同温度下的速率分布函数，见图2。图2中清晰地显示，随着温度的升高，速率分布曲线变得平缓，峰值右移，向高速区域扩展，其最概然速率增大，说明温度越高，分布在高速率区间的分子数所占百分比就越大，这就是通常所说的温度越高，分子运动越剧烈的真正含义。由于归一化条件的约束，其速率分布函数（峰值）减小，因此分布曲线在宽度增大的同时，高度降低，分布也就越趋均匀，整个曲线将变得“较平坦”。对于温度为300K对应的曲线速率超过1 200m／s的分子数趋于0，而对于温度为600K对应的曲线速率要大于1 600m／s才趋于0。

图2 不同温度下麦克斯韦速率分布曲线

以质量为参数对（3）式进行编程时，只需修改文件maxwellsl.m中的温度和气体分子质量即可。在温度一定的情况下，不同分子的质量是参数，麦克斯韦速率分布的函数曲线会随质量这个参数的改变而有所改变。图3中分别是氖气、氮气、氧气和氟气在同一温度（300K）下处于平衡态时的速率分布曲线，由图清晰地看到随着气体分子质量的增加，其最概然速率减小，但其速率分布函数的峰值增大，说明在相同速率间隔内，向着各个方向运动的速率大的分子数量比较多，速率小的分子数量比较少，也就是说：在相同温度下，质量较大的分子运动的剧烈程度较小。平均平动动能仅与平衡态下的温度有关［10］，因此，分子质量越小，其运动就越剧烈，最概然速率也越大，分布在高速率区间的分子数百分比就越大，分布也越趋均匀。

图3 同一温度不同气体的麦克斯韦速率分布曲线

3 一定速率范围内的分子数占总分子数的百分比

根据麦克斯韦速率分布可求任何一个速率段的分子数占总分子数的比例，设总分子数为N0，分子速率在区间0～v的分子数占总分子数的百分比可表示为［11］

（5）代入（4），得

利用Matlab中的梯形累积函数cumtrapz可计算（6）式积分值，编程语句如下：

将Matlab数值计算结果作图得到图4，从图中看到，分子速率在0～v之间的分子数占分子总数的比例随着v单调增加，这是因为v越大，0～v之间的分子数就越多。图4给出了三种典型速率处的分子百分率，当x＝v／vp＝l即v＝vp时，分子数占分子总数的比例是42.8%，分子数小于总分子数的一半，而分子速率大于最概然速率vp的分子占总数的比例是57.2%，超过总分子分子速率小于平均速率的分子数占分子总数的比例是53.31%，分子数超过总分子数的一半；当x方均根速率的分子数占分子总数的比例是60.84%；当x＝2.5即v＝2.5vp时，分子速率从0到v的分子数就占了全部分子数的绝大部分。

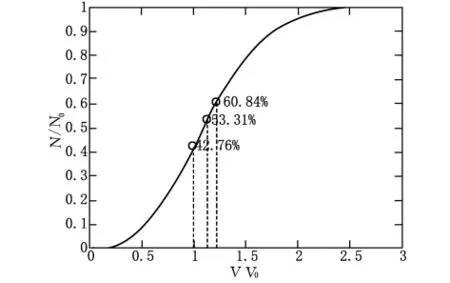
图4 0～u之间的分子数占总分子数的比例

4 结 论

通过Matlab软件在大学物理热学部分的麦克斯韦分布律的教学中的实例应用，可见该软件在大学物理教学中有其独特的优势：第一，由Matlab绘制的分布曲线具有精确的位置关系、描述准确的数据，引入课堂带来生动感、真实感，起到非常好的教学辅助作用；第二，利用Matlab可以很方便地将数值计算的结果可视化，可以利用Matlab解物理方程及微积分问题，从而摆脱枯燥乏味的数学运算；第三，可以利用Matlab强大的绘图功能把复杂物理公式中的规律直观地展现出来，从而更深入地理解其中的物理奥秘。总之，通过Matlab软件的使用可以有效地提高教学效率，让学生更直观地理解物理原理，可以降低实验教学的成本，提高教学效果。

［1］张星辉.在大学物理教学中使用Matlab制作图像和动画的几个实例［J］.大学物理，2004，23（9）：59－62.

［2］丁益民，陈倩.基于Matlab的RLC电路暂态过程的模拟［J］.大学物理实验，2011，24（2）：45－47.

［3］马文蔚.物理学（下册）［M］.北京：高等教育出版社，2006.

［4］姜辉，刘艳凤，马提宝.MATLAB软件在大学物理教学中的应用［J］.吉林师范大学学报：自然科学版，2009（2）：83－85.

［5］王明美.MATLAB在麦克斯韦速率分布律教学中的应用［J］.合肥师范学院学报，2010，28（6）：40－42.

［6］周群益，侯兆阳，刘让苏.MATLAB可视化大学物理学［M］.北京：清华大学出版社，2011.

［7］曾立.Matlab在大学《热学》课程教学中的应用［J］.广西师范学院学报：自然科学版，2010，27（3）：103－105.

［8］宿刚，郑敏章，丛令梅.Matlab在大学物理课程教学中的应用［J］.浙江海洋学院学报：自然科学版，2008，27（2）：241－244.

［9］程守洙，江之永.普通物理学［M］.6版.北京：高等教育出版社，2006.

［10］杨咏东，王君美.MATLAB在大学物理热学多媒体课件制作中的应用［J］.物理通报，2012（5）：76－78.

［11］李小燕，冯卓宏，邱俊才.Matlab在大学物理教学中的应 用 ［J］.实验技术与管理，2010，27（11）：124－126.

［12］吴百诗.大学物理（下册）［M］.西安：西安交通大学出版社，2008：116.