用光电效应测普朗克常量实验智能数据处理系统的开发

刘万红，江兴方，江 鸿

（1.华东师范大学出版社，上海 200062；2.常州大学，江苏 常州 213164；3.常州天合光能有限公司，江苏 常州 213031）

1900年德国物理学家普朗克在研究黑体辐射规律时，发现了普朗克常量，从此物理学进入了现代物理的时代［1，2］。爱因斯坦总结光电效应为（1）饱和光电流与光强成正比；（2）光电效应存在一个截止频率γ0，当入射光的频率低于γ0时，不论光的强度如何，都没有光电效应产生；（3）光电子的动能与光强无关，但与入射光的频率成线性关系；（4）光电效应是“瞬时”的，当入射光的频率大于阀频率时，一经光照射，立刻产生光电子。普朗克常量可以根据爱因斯坦方程Ek＝hγ-A来确定。式中为金属表面逸出的电子最大初动能值；A为逸出功；γ为照射光的频率。为了准确测得到普朗克常量，实验采用汞灯光谱中光强较强的五种波长365.0nm，404.7nm，435.8nm，546.1nm，577.0nm制成的滤色片，其相应的频率为8.214×1014Hz，7.408×1014Hz，6.879×1014Hz，5.490×1014Hz，5.196×1014Hz。文献［1］考虑了光电效应中的热效应，利用外推法确定普朗克常用量；文献［2］提出了采用拐点法、补偿法和零电流法对于ZKY－GD－3型实验仪器测得的结果，采用Advanced grapher软件对三组每组5个滤色片测得的相应遏止电压值进行了计算，得到了普朗克常量并分析实验不确定度。文献［3］利用ZKY－GD－3型实验仪器测得的5个滤色片与相应的遏止电压值计算普朗克常量并分析实验不确定度。文献［4］采用XD－P3型光电效应实验仪测得的5个滤色片与相应的遏止电压值计算普朗克常量并分析实验不确定度。文献［5］采用了拟合法、逐差法和图解法根据5个滤色片与相应的遏止电压值计算普朗克常量并分析实验不确定度。以上文献共同之处是采用了5个滤色片与相应的遏止电压值，来个别计算普朗克常量并分析实验不确定度，如表1所示。本课题着重解决的是，一般性的“用光电效应测普朗克常量”智能化实验数据处理系统。区别在于（1）只要用户将遏止电压值输入到相应的滤色片位置，一按“智能绘图”钮立即进行计算，显示拟合直线及其斜率，显示普朗克常量及其不确定度；（2）输入的遏止电压值的个数只要大于等于3，即可能是3个，4个或者5个都可以进行计算；（3）所显示的不确定度严格按不确定度取1位，不确定度的那一位与有效数字末位对齐，不确定度只进不舍，有效数字四舍五入。

1 用光电效应测定普朗克常量实验

光电效应实验［6－12］电路图如图1所示，阴极K具有高电势，而且阴极K的电势可以调节，不难测出阴极逸出的电子流在反向电压作用下的伏安特性曲线，如图2中U＜0的部分。

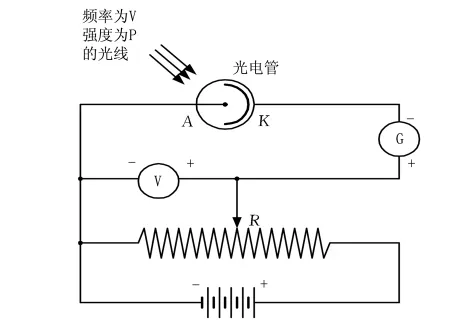
图1 测普朗克常数原理图

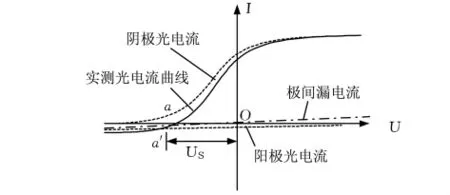
图2 伏安特性曲线

由于光电管的极间漏电、入射光照射阳极或入射光从阴极反射到阳极之后都会造成阳极光电子发射，它们虽然很小，但是构成了光电管的反向光电流，如图2中虚线（阳极光电流）和点画线（极间漏电流）。由于它们的存在，使光电流曲线下移，如图2中实线所示（实测光电流）。当反向光电流比正向光电流小得多时，曲线下移可以忽略。假定反向电压为Us时，所有光电子都不能到达阳极，光电流为零，则Us被称为光电效应的截止电压，即

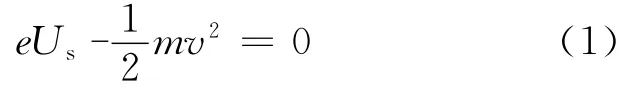
从而可得

由于金属材料的逸出功A是金属的固有属性，对于给定的金属材料，A是一个定值，它与入射光的频率无关。具有截止频率γ0的光子的能量为A＝hγ0，因此

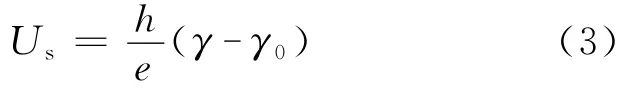
截止电压Us是入射光频率γ的线性函数。用不同频率γ的光照射图1中的光电管，可以得到与之相对应的不同频率下的伏安特性曲线和相应的截止电压Us。作Us～γ关系曲线。若是直线，就证明了爱因斯坦光电效应方程的正确性。并由该直线的斜率，即可求出普朗克常数h（电量

实验的重点就是精确地测定不同频率的光相应的截止电压Us，并且作出相应的Us～γ关系曲线，确定直线的斜率，求出普朗克常量。

2 智能实验数据处理系统的开发

在文献［2－5］测得的5个滤色片与相应的遏止电压值如表1所示，在此基础上，开发一个“用光电效应测普朗克常量”智能化实验数据处理系统，如图3和图4所示。

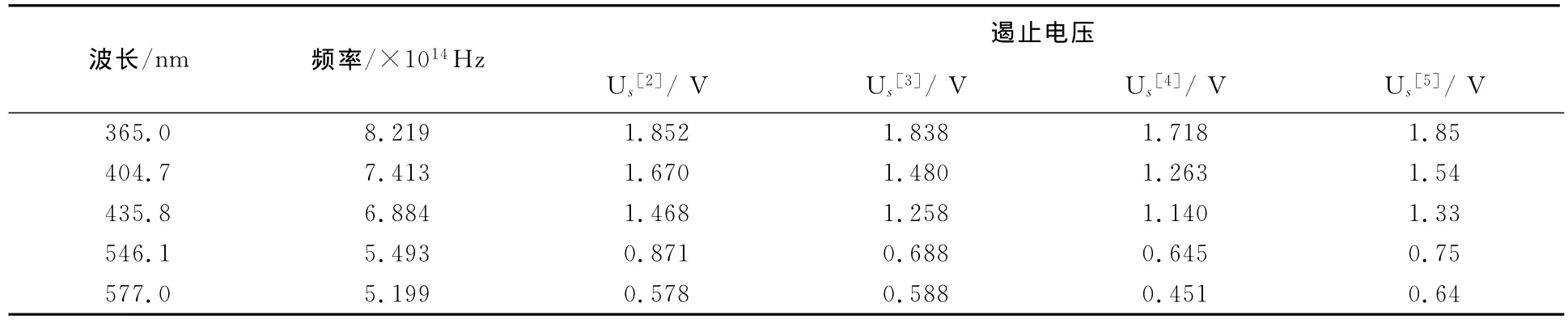
表1 “用光电效应测普朗克常量”实验的不同实验数据

2.1 界面设计

“用光电效应测普朗克常量”智能化实验数据处理系统包括标题“用光电效应测普朗克常量”，表格包括三行，第一行为入射光波长，分别是“365.0nm”、 “404.7nm”、 “435.8nm”、“546.1nm”和“577.0nm”，第二行为相应的入射光频率，单位为“×1014Hz”，大小分别为“8.219”、“7.413”、“6.884”、“5.495”、“5.199”，第三行设计有5个可填域，用于用户输入相应滤色片的遏止电压值。

表格下方是拟合直线的斜率，普朗克常量计算结果，包括有效数字与不确定度。

普朗克常量显示域下方即界面中心位置是坐标轴系统，水平坐标为入射光频率，竖直坐标为遏止电压的绝对值，5个红色点表示实验数据点，直线为拟合直线。

在坐标轴系统下面是“智能绘图”、“缺省”、“清除”三个按钮。其中“清除”按钮的功能是，当点击该按钮，清除所有显示域的数数据，包括用户输入的遏止电压数据、拟合直线斜率、计算的普朗克常量及其不确定度。其中“缺省”按饭的功能是，用于演示该智能数据处理系统时，免去数据一个一个输入，可以节省演示的时间。其中“智能绘图”按钮就是本课题的重点，就是智能计算普朗克常量，如图3和图4所示中的“智能绘图”按钮的功能是读取用户输入的相应滤色片的遏止电压值，进行统计分析，利用最小二乘法拟合直线，计算直线斜率、计算普朗克常量及其不确定度，显示相应滤色片的遏止电压值的实验点，显示拟合直线，而且分析普朗克常量的不确定度，取不确定度1位，且与有效数字的末位对齐，不确定度只进不舍，有效数字四舍五入。

2.2 “智能绘图”按钮程序设计

（1）设置数组用于存放频率、遏止电压。采用“非空加一”统计法统计出输入的遏止电压个数，即先令n＝0，按数组顺序读一个判断一个，非空则加1。

（2）判断输入的实验数据个数n。当n＞2时，即3，4，5则进行直线拟合，否则智能系统［8］显示“请将实验数据输入完整”。

（3）当n＝3，4，5时，重新设置数组，分别将频率作为自变量，相应的遏止电压值为应变量，智能系统在笛卡儿坐标下，采用最小二乘法，计算拟合直线的斜率与截距。

（4）估计拟合直线斜率k的不确定度，根据不确定度的大小，保留拟合直线斜率的位数，确保拟合直线k的最低位就是不确定度的最高位。再采用计算普朗克常量h，其中e为电子电量，即然后估计普朗克常量的不确定度，不确定度取一位，且与普朗克常量的末位对齐，不确定度只进不舍，有效数字四舍五入。

（5）在智能系统界面上的显示域中显示斜率k、普朗克常量及其不确定度。

（6）进行坐标变换，将笛卡尔坐标转换成Multimedia ToolBook坐标，采用最小二乘法计算拟合直线斜率与截距。

（7）在智能系统界面上显示实验点与拟合直线，实验点用红色圆点表示，拟合直线用黑色直线表示。图3为“智能绘图”按钮编程流程图。

2.3 试验结果

开发的“用光电效应测普朗克常量”智能化实验数据处理系统，将表1中的实验数据输入后得到文献［2－5］计算相同的结果，特别是当将文献［2］中的实验数据少填1个输入后，得到了h＝结果，如图4所示；将文献［4］中的实验结果少填2个输入后，得到了h＝结果，如图5所示。

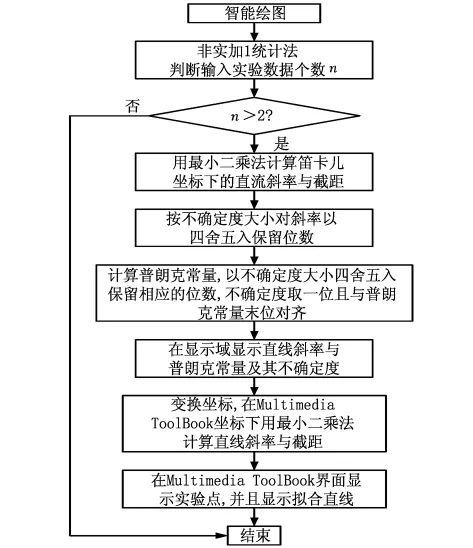
图3 “智能绘图”编程流程图

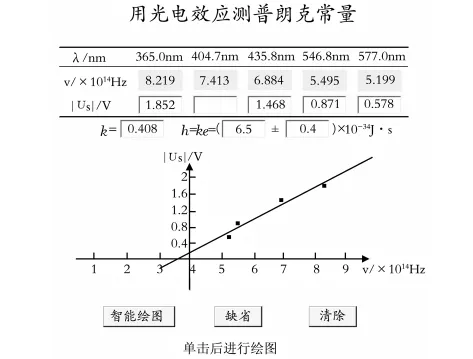
图4 智能系统计算结果（4个实验数据）

图5 智能系统计算结果（3个实验数据）

3 结 论

在“用光电效应测普朗克常量”实验数据处理中，基于多媒体著作工具 Multimedia ToolBook开发的智能化实验数据处理系统直接地显示拟合直线、普朗克常量及其不确定度，快速准确。其智能体现在只要输入3个或者3个以上的滤色片相应的遏止电压，系统就能统计出相应的自变量与应变量，采用最小二乘法拟合直线，求出斜率，并显示出普朗克常量及其不确定度，一目了然。其中特别是采用了“非空加一”方法将没有输入遏止电压的域滤去，统计出输入遏止电压值的个数，如果输入遏止电压值的个数少于3个系统提示“请将实验数据输入完整”。如果输入遏止电压值的个数大于等于3，则系统将输入输入遏止电压值的滤色片频率值计为自变量，将遏止电压值计为应变量，再采用最小二乘法进行直线拟合，这一方法可适用于相关实验的数据处理中去。

［1］杨际青.改进的光电效应测量普朗克常量外推法实验［J］.大学物理，2003，22（12）：38－42.

［2］吴丽君，李倩.光电效应测普朗克常数的三种方法［J］.大学物理学实验，2007，20（4）：49－52.

［3］王云志，赵敏.光电效应的数据处理及误差分析［J］.大学物理实验，2011，24（2）：93－95.

［4］刘绒侠，王党社，彭首军.用Origin软件处理物理实验数据［J］.大学物理实验，2008，22（2）：91－93.

［5］黄德润.试论大学物理实验数处理的选取［J］.福建教育学院学报，2005（1）：144－146.

［6］Shisong Li，Bing Han，Zhangkun Li，et al.precisely measuring the Planck constant by electromechanical balances［J］.Measurement，2012，45：1－13.

［7］王瑗，潘葳，李向亭.基于发光二极管的普朗克常量的测量［J］.物理实验，2010，30（10）：5－7.

［8］江兴方，谢建生，唐丽.物理实验［M］.北京：科学出版社，2011.

［9］杨达晓，唐海燕，杨耀辉.Origin软件在普朗克常量测定实验中的应用［J］.大学物理实验，2010，23（5）：67－69.

［10］黄勇.测普朗克常量实验数据处理［J］.物理实验，2011，31（3）：25－28.

［11］Jiang Xingfang，Li Feng，Li Xiang，Ouyang Jifang.Making of intelligent data processing system of the experiment in the coefficient determination of the thermal conductivity［J］.Procedia Engineering，2011，15：2892－2896.

［12］代海洋.光电效应测定普朗克常量实验的计算机仿真的教学探讨［J］.大学物理实验，2012（5）：75－77.