破片撞击装药点火实验和数值模拟＊

孙宝平，段卓平，张海英，刘 彦，黄风雷

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

装药在破片或子弹撞击作用下的响应是装药安全性研究中的重点。P.M.Howe［1］、王树山等［2］、A.R.Gushanov等［3］进行了破片撞击装药实验，得到了破片撞击炸药起爆的临界速度，认为炸药起爆的原因可分为冲击起爆和机械刺激起爆2种。J.C.Foster等［4］研究了摩擦、剪切、破片撞击等机械刺激作用下炸药的点火问题，认为炸药点火燃烧可能引发严重事故，这是侵彻弹药发生失效的重要原因。实际上，战场环境中装药常受到破片撞击作用而引发炸药点火，因此，破片撞击装药点火机理研究不仅在装药安全性方面有重要理论意义，而且对弹药的低易损性设计和反导战斗部的技术设计有重要指导意义。

1 破片撞击装药实验

以JO－8炸药为研究对象，装药尺寸为∅80mm×80mm，质量约为735g。利用虫胶将装药粘装在无缝钢筒内，一端面由聚四氟乙烯底座封闭，另一端面为自由面（破片撞击面）。无缝钢筒壁厚15mm，材料为45钢。以钨珠作为破片，钨珠直径为6mm，质量约为2.18g。驱动（发射）装置选用某所自行设计的发射枪，发射火药为质量为1g的2＃小粒黑与不同质量的4／7火药的混合炸药，通过调整4／7火药的质量控制破片的速度。发射火药燃烧生成大量气体，密闭的气体迅速膨胀驱动弹托／钨珠在枪膛内运动，安装在枪口的脱壳器阻拦弹托，迫使弹托与钨珠完全分离，保证了测速靶能够准确测得破片速度，图1为发射枪及脱壳器装置。发射枪安装瞄准装置，发射前均使用瞄准装置调整装药位置，发射枪口至装药中心的距离为1.3～1.5m，能够确保破片着靶点位于装药撞击面的中心。测速靶的靶纸为2层锡箔纸，中间由绝缘纸相隔，测速前2锡箔纸完全绝缘，锡箔纸与计时仪连接。当破片穿过测速靶纸时，2层锡箔纸瞬间导通，计时仪获取导通信号（断－通），已知2张靶纸间的距离，可算出破片速度。

另外，实验中还使用高速摄影用以观察装药受到破片撞击后的响应情况以及校核破片速度等。由于装药受到钢筒约束，当破片速度高于起爆临界速度时，装药发生爆炸，因此为防止爆炸产物对发射枪的破坏，将装药放在掩体内进行实验，发射枪与装药之间装有防护装置，实验现场如图2所示。

实验中，首先从发射枪发射高速破片撞击装药开始实验，而后采用升－降法调整破片速度，获取装药起爆和点火的临界破片撞击速度范围。表1给出了破片撞击装药的实验结果，其中v为网靶测得的破片撞击速度。实验结果评定分为爆炸、爆燃和装药破损3个等级。为方便对比，表1中按照破片速度由高到低排序。

图1 发射枪及脱壳器装置Fig.1 Devices of launcher and sheller

图2 破片撞击装药实验现场Fig.2 Experimental site for fragment impacting charge

表1 破片撞击装药实验结果Table1 Experimental results of fragment impacting charge

破片速度为大于500.3m／s时，无缝钢筒完全破碎，回收到钢筒的碎块（见图3），高速摄影拍摄到装药发出强光，可判定装药发生爆炸。破片速度为492.5和470.0m／s时，装药均未发生爆炸，回收到的无缝钢筒均完好（见图4），高速摄影拍摄到装药发出强烈火光，筒内无残留装药。破片速度为492.5m／s时，观察到防护装置上散落有少许炸药粉屑，未发现炸药残块；破片速度为470.0m／s时，地面有少许炸药残块。综合判定装药均发生了爆燃反应，前者爆燃反应较后者剧烈。破片速度为456.1和420.1m／s时，实验现场均未听到装药发生反应的声响，高速摄影也均未拍摄到火光，装药表面有少许崩落，未见到装药点火烧蚀的痕迹，综合判定装药未发生点火反应，仅发生撞击破坏。测得破片侵入装药深度分别为24.0和14.8mm，图5给出了撞击速度为420.1m／s时装药的破损情况。

图3 破片速度为v＝1 093.0m／s回收的钢筒碎块Fig.3 Recycled fragments of steel tube at the impact velocity of 1 093.0m／s

图4 破片速度为v＝492.5m／s时回收的空钢筒Fig.4 Recycled empty steel tube at the impact velocity of 492.5m／s

图5 破片速度为v＝420.1m／s时钢筒内装药破损Fig.5 Damaged charge in steel tube at the impact velocity of 420.1m／s

综合上述实验结果和分析，装药起爆的临界撞击速度介于装药爆炸的最小撞击速度与装药爆燃的最大撞击速度之间，起爆阈值速度范围为492.5～500.3m／s。装药点火的临界破片撞击速度介于装药爆燃的最小撞击速度与装药破损的最大撞击速度之间，点火的阈值速度范围为456.1～470.0m／s。

2 数值模拟

2.1 节点约束－分离法

在数值模拟炸药剪切、撞击等过程中，炸药单元承受较大的变形，易出现严重的网格扭曲和畸变，通常炸药材料采用欧拉算法，该算法可以解决网格的大变形问题，但是不能够精确定义炸药剪切破坏的物质边界，同时也影响炸药破坏面的温度描述。采用拉格朗日算法计算大变形和破坏问题时一般采用侵蚀算法，即将炸药设为连续体，当炸药受到拉压后发生严重变形，达到指定数值后删除单元网格。这样可避免计算中出现负体积等问题，但这与实际炸药裂纹生成、扩展或者损伤断裂等有很大差别，并且在删除单元后，炸药的热学（温度）计算会发生错误而终止，或者热力学计算结果为伪温度。因此，应寻求描述炸药力学破坏和热学问题的新方法。

节点约束－分离法［5］是指相邻单元坐标相同的节点相互独立，彼此约束相对自由度，通过定义的断裂准则控制节点分离，当单元力学状态满足断裂准则时，节点之间的约束失效，相邻单元坐标相同的节点相互分离。一般以塑性应变作为断裂准则，当塑性应变大于预设的失效应变时，节点相互分离。该方法可以描述材料裂纹的生成、扩展等现象和特性。实际上，节点约束－分离是有限元断裂在数值模拟中的概念，使用的仍然是拉格朗日算法，它既可以避免传统有限元方法中结构断裂、网格严重扭曲以及畸变导致的无法计算问题，又能够克服SPH方法边界处理模糊等困难。采用节点约束－分离法进行数值模拟时，一个重要的参数是塑性失效应变，该值直接影响到数值模拟中炸药力学破坏效果的描述。一般情况下，失效应变通过材料的断裂实验测得。

图6 破片撞击装药1／2计算模型Fig.6 1／2calculation domain for fragment impacting charge

2.2 计算模型

破片、装药、钢筒等呈对称性，为减少计算时间，建立1／2计算模型，如图6所示。为了重点考察破片撞击区域装药的破坏和点火，精划装药撞击破坏区的网格，尺寸为0.2mm。单元尺寸对撞击剪切数值模拟有较大影响，经过数值模拟试算，本文计算模型的单元尺寸为0.2mm能够客观地描述破片撞击装药破坏和点火反应，其计算结果与单元尺寸为0.1mm时的计算结果趋于一致。

2.3 材料模型

对炸药的力学属性采用热弹塑性本构方程［6］描述：

式中：T为由炸药热弹塑性材料和热分解放热反应共同引起的炸药温度为总应变率为热应变率；α为线膨胀系数；δij为Kronecker符号；是与温度相关的弹性矩阵C的分量，C的表达式为：

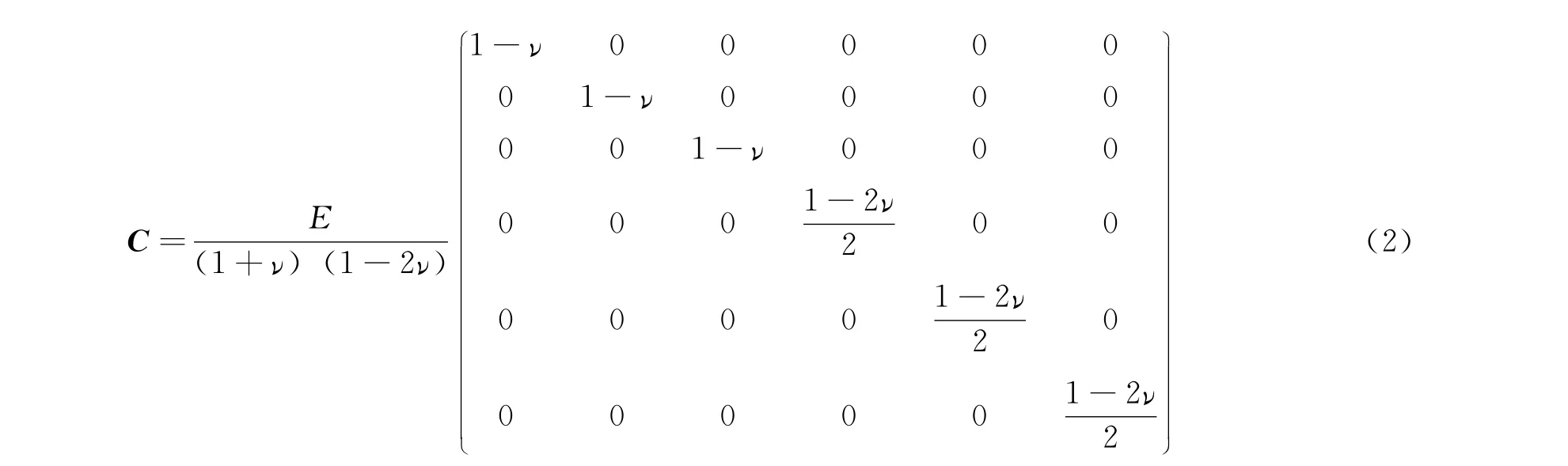
式中：ν是泊松比。

材料屈服函数为：

式中：sij为应力偏量；σy（T）＝Ep（T）＋σ0（T）为屈服应力为等效塑性应变；σ0为初始屈服应力；Ep为塑性硬化模量，σ0和Ep均为温度的函数。

对炸药热物理属性采用各向同性热传导模型描述，热传导微分方程为：

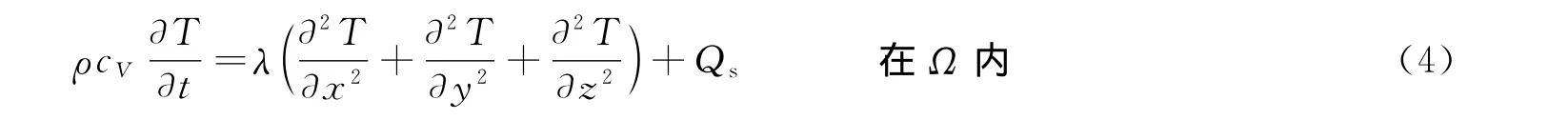
式中：ρ为材料密度；cV为材料比定容热容；T 为温度；λ为热导率；Qs为材料内部的热源，＋Qt，η为功转热比率，Qt为炸药热分解放热量；Ω为温度场空间。

对于炸药材料而言，温度上升会引起材料的热分解放热反应，化学动力学方程采用Arrhenius方程表示。由于点火时反应物的转变率很低，因此假定反应物从整个自热到点火的过程中反应初始浓度变化可忽略不计，炸药热分解放热量为：

式中：Q为反应热，A为指前因子，Ea为活化能，R为气体常数。

炸药热学与力学耦合计算的基本方程为：

装药为JO－8炸药，其主要成分HMX、高聚物粘结剂和蜡钝感剂的质量分数分别为95%、3.7%和1.3%。JO－8炸药的失效应变值为0.66%［7］，点火温度为610～620K。JO－8炸药的热力学参数［7］为：ρ＝1.83g／cm3，λ＝0.36W／（m·K），cV＝1 010J／（kg·K），A＝5.9×1014s－1，Ea＝1.68MJ／mol，Q＝2.284MJ／kg。数值计算中，将装药简化为各向同性体。

对破片（钨珠）、钢筒和钢锭等采用塑性随动硬化本构模型描述，热学采用各向同性热传导模型，材料力学和热学参数［8］如表2所示。

表2 钨和45钢材料参数Table2 Parameters of tungsten and 45steel

3 计算结果

3.1 装药点火计算结果

图7给出了不同时刻装药撞击破坏和温度分布，图中的温度为炸药节点的温度，炸药单元的温度为该单元各个节点的平均温度。从图中可以看出：3.60μs时装药发生弹塑性变形；11.69μs时，破片附近装药生成的热量来不及向外传递时，局部装药温度骤升，装药发生点火反应；紧接着在11.80μs时，点火单元的邻近单元依次达到点火温度，发生点火反应。破片撞击装药实验结果同样表明，当破片速度为470.0m／s时，装药发生爆燃反应。模拟结果与实验结果吻合较好。

图7 破片撞击速度为470.0m／s时装药温度分布Fig.7 Evolution of temperature distribution of charge at the impact velocity of 470.0m／s

图8给出了炸药在破片撞击条件下节点约束失效和局部的网格变形，可以看出裂纹的形成以及破损情况。如果数值模拟不采用节点约束－分离法，炸药单元网格将发生畸变，导致计算终止，不能模拟出破片对炸药撞击损伤和破坏等实际发生的现象。

图8 破片撞击炸药后的网格变形和节点分离Fig.8 Mesh deformation and node breaking of explosive impacted by fragment

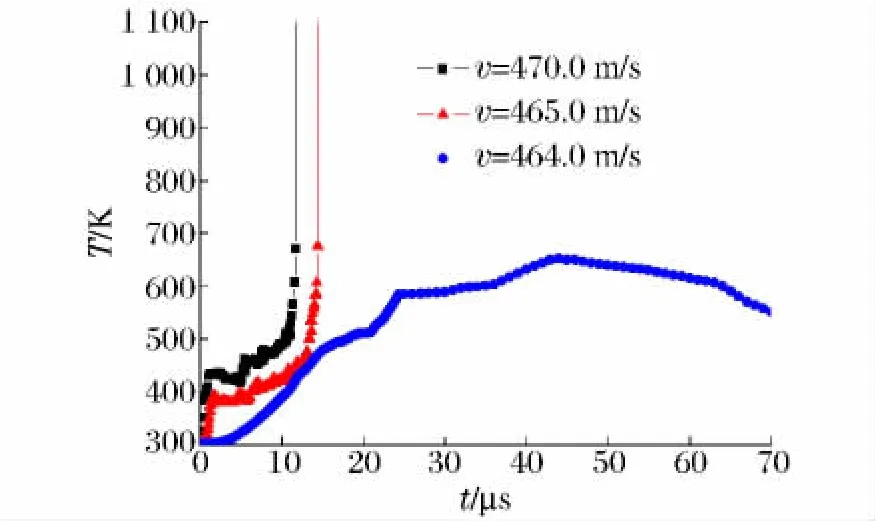
图9 最高温度单元的温度曲线Fig.9 Temperature in highest－temperature elements

图9给出了不同撞击速度下装药中最高温度单元的温度曲线。可以看出：撞击速度为470.0m／s时，装药发生点火反应，点火时间为11.69μs，点火温度为671 K；撞击速度为465.0m／s时，装药发生点火反应，点火时间为14.40μs，点火温度为676K；撞击速度为464.0 m／s时，装药最高温度为653K，而后温度趋渐缓和，未能达到点火温度，未发生点火反应。因此，破片撞击JO－8装药点火的临界撞击速度为464.0～465.0m／s。破片撞击装药实验得到的临界撞击速度为456.1～470.0m／s，模拟结果与实验结果基本一致。

3.2 装药破损的计算结果

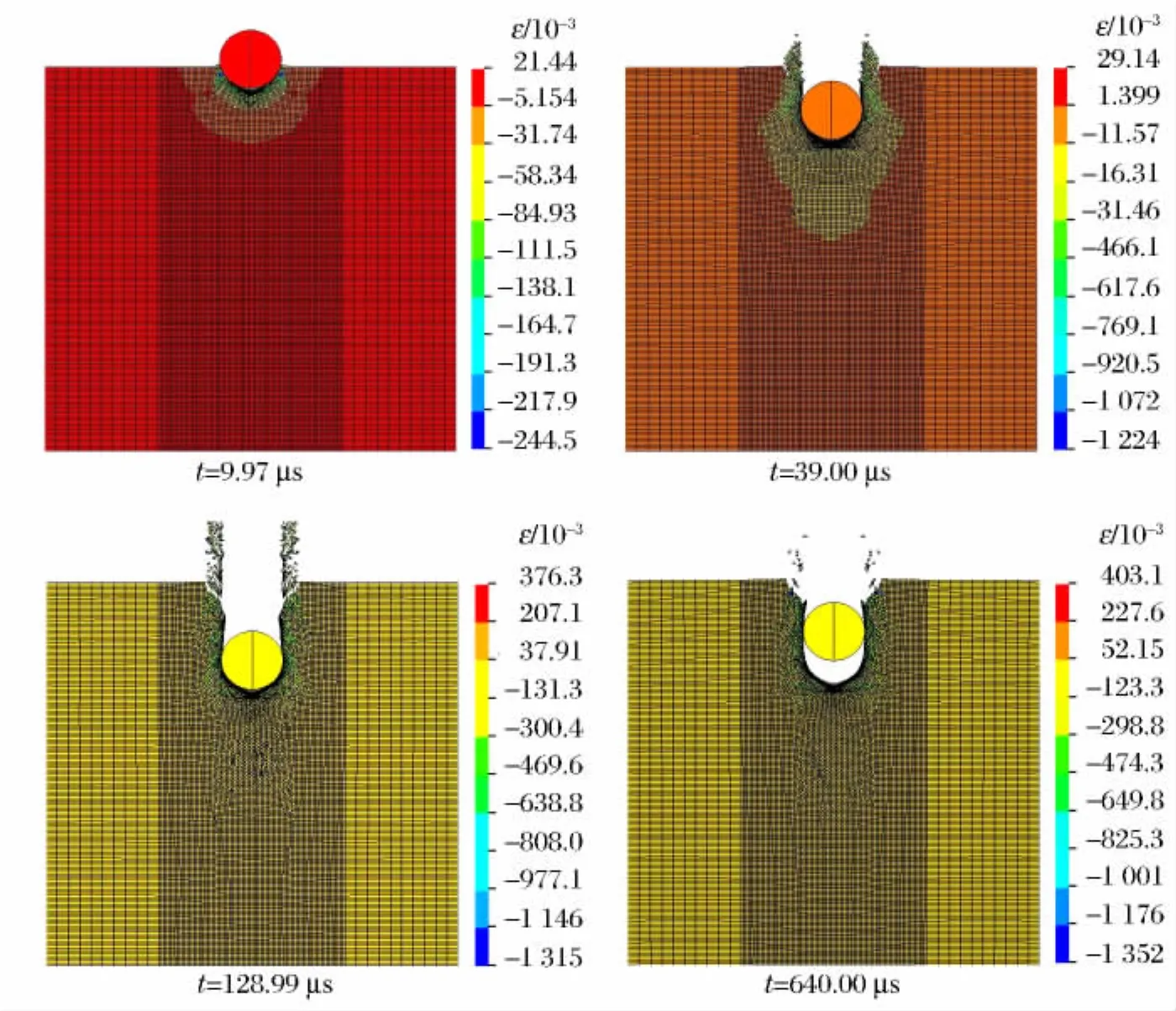
图10 破片撞击速度为456.1m／s时装药应变Fig.10 Evolution of strain of charge at the impact velocity of 456.1m／s

当破片撞击速度为456.1m／s时，实验中装药未发生点火反应，仅受到撞击破坏，数值模拟也得到相同的结果，从图10可以看出破片撞击装药时单元的应变以及网格变形态势。装药塑性应变值达到指定失效应变后，装药单元的节点分离，其中脱离装药的部分单元由装药破损处向外飞散（图中为向上）。

图11 破片速度曲线Fig.11 Fragment velocity curve

图11为破片撞击速度为456.1m／s时破片的速度历程曲线，在侵入装药的过程中，破片速度逐渐下降，在99μs时，速度降为0，破片侵入装药深度为23.3mm；而后破片反弹，在640μs时，破片反弹速度为10.0m／s（方向向上），发生弹性变形的装药单元在破片反弹后释放了弹性应变能，破片侵入装药深度减小，最终深度为21.1mm。实验测得破片侵深为24.0mm，实验结果和数值模拟结果吻合较好。

4 结 论

破片撞击装药点火实验中采用升－降法得到了临界速度范围。采用节点约束－分离法，利用热弹塑性材料模型和化学动力学方程模拟了在破片撞击下装药的点火反应和破坏行为，实验结果和数值模拟结果吻合较好。

（1）采用节点约束－分离法可以描述装药的裂纹生成、扩展、断裂破坏等现象，模拟过程可清晰显示装药的破坏行为。

（2）在装药点火反应中考虑炸药的热分解放热反应，热弹塑性材料模型和化学动力学方程能够描述机械刺激下装药点火反应。

［1］Howe P M.On the role of shock and shear mechanism in the initiation of detonation by fragment impact［C］∥Proceedings of the 8th International Symposium on Detonation.Albuquerque，USA，1985：1150－1159.

［2］王树山，李朝军，马晓飞，等.钨合金破片对屏蔽装药撞击起爆的实验研究［J］.兵工学报，2001，22（2）：189－191.Wang Shu－shan，Li Chao－jun，Ma Xiao－fei，et al.An experimental study on the initiation of covered charge impacted by tungsten alloy fragments［J］.Acta Armamentarii，2001，22（2）：189－191.

［3］Gushanov A R，Volodina N A，Belov G V，et al.Numerical simulation of experiments on the low－velocity impact on HMX－based HE using explosive transformation initiation kinetics［J］.Journal of Energetic Materials，2010，28（Suppl 1）：50－65.

［4］Foster J C，Christopher F R，Wilson L L，et al.Mechanical ignition of combustion in condensed phase high explosives［C］∥Shock Compression of Condensed Matter－1997：Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter.Amherst，MA，USA，1997：389－392.

［5］孙宝平，段卓平，皮爱国，等.SHPB剪切炸药点火数值模拟［J］.兵工学报，2012，33（增刊1）：62－68.Sun Bao－ping，Duan Zhuo－ping，Pi Ai－guo，et al.Numerical simulation of shear ignition of explosives in SHPB［J］.Acta Armamentarii，2012，33（Suppl 1）：62－68.

［6］Hallquist J O.Ls－dyna theory manual［M］.Livermore，USA：Lawrence Livermore National Laboratory，2006.

［7］西安近代化学研究所.JO－8炸药鉴定验收报告［R］.西安：西安近代化学研究所，2001：36－48.

［8］马庆芳，方荣生.实用热物理性质手册［M］.北京：中国农业机械出版社，1986：81－652.