球对称形式物质点法及其在水下爆炸中的应用＊

陈卫东，杨文淼，严 涵，张丰超

（哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨 150001）

对水下爆炸问题的研究一直是爆炸冲击动力学领域研究的热点，在军事工业以及民用建设领域都具有重要的意义。水下爆炸涉及高能炸药的爆轰、冲击波在水介质中的传播和气泡的脉冲等一系列复杂过程，理论与实验研究都具有一定的局限性。数值研究具有低成本、可重复和过程细节易于捕捉等优势，在水下爆炸研究领域中起着越来越重要的作用。水下爆炸过程存在大变形问题，使得基于随体网格的拉格朗日方法产生严重的网格畸变，影响计算精度，甚至使计算无法进行，所以大都采用具有空间固定坐标的欧拉方法对水下爆炸进行数值分析［1－4］。但欧拉方法不易观察材料的变形历史，并且物质界面的处理也是欧拉方法面临的一个难题，这些都限制了欧拉方法的应用。近年来无网格方法如SPH（smoothed particle hydrodynamics）、MPM（material－point method）等因为不存在网格畸变，可以很自然地处理大变形问题，在爆炸冲击问题中得到了广泛应用［5－12］。MPM由流体动力学领域的PIC（particle－in－cell）法发展而来，兼具拉格朗日法和欧拉法的优点，在处理大变形以及多介质耦合问题时具有突出优势［13］。MPM将问题域离散成一系列携带材料性质的物质点集，对于三维水下爆炸问题，尤其是三维远场爆炸问题，问题域的空间尺度是巨大的，并且随着问题维度的增加，物质点数量也会成指数增长。对于远场水下爆炸，人们关心的是结构在爆炸冲击波作用下的冲击响应，而对爆炸冲击波在水介质中传播过程的计算会占用大量的计算资源，严重影响求解效率。当忽略界面或结构的影响时，水下爆炸产生的冲击波在水介质中具有球对称性。利用水下爆炸这一特点，将冲击波在自由场中的传播过程简化为一维球对称模型进行计算，这样可以在保证求解精度的前提下提高计算效率。基于AUTODYN中的映射求解思想［14］，建立了基于物质点法的水下爆炸重映射求解模型，当爆炸冲击波到达界面或者结构之前，采用一维球对称模型进行计算，然后将计算结果映射到三维模型中，并将各计算量作为初值在三维模型中继续完成计算，有效避免了计算资源在冲击波传播过程上的消耗。

本文中，首先推导一维球对称形式的物质点法，然后对球形炸药水下爆炸过程进行数值计算，并与Cole经验公式［15］以及DYNA计算结果进行比较，结果吻合较好，验证了一维球对称形式物质点法的准确性。在此基础上，提出了基于物质点法的重映射求解算法，将一维球对称结果作为初始条件映射到笛卡尔坐标系下的三维模型中，从而可以在三维模型中继续求解冲击波的传播以及结构的冲击响应过程。

1 球对称形式的物质点法

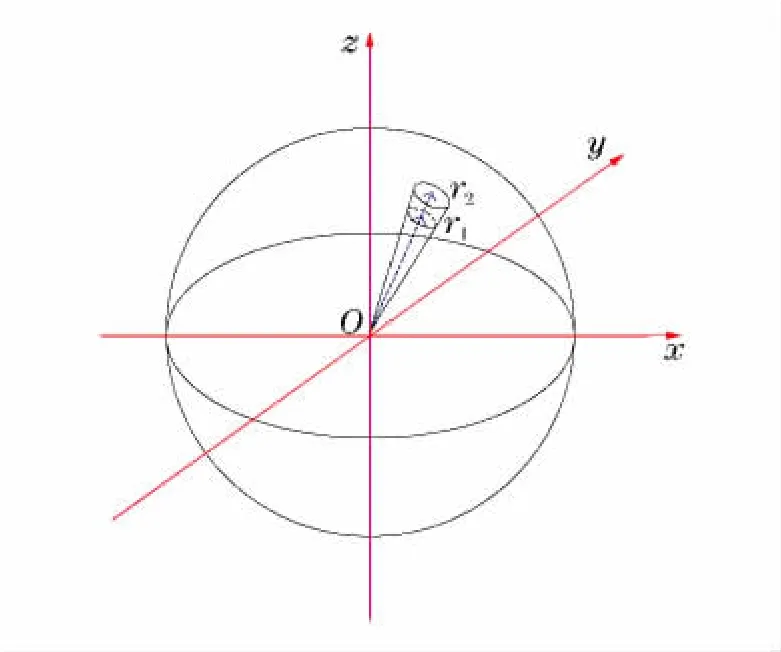
图1 球坐标系下的离散单元Fig.1 Discrete elements in spherical coordinate system

在一维球对称坐标下离散的质点质量是不均匀的，其质量大小与质点的密度分布以及径向坐标都有关系。如图1所示，在球坐标系下沿径向离散的单元坐标为r1和r2，单位立体角内离散单个质点的质量为：

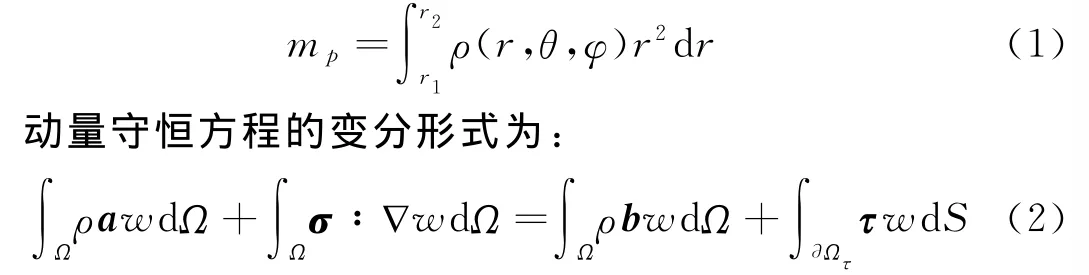
式中：ρ为密度，a为加速度，σ为柯西应力张量，b为体力，τ为边界外力，w为试函数。

在MPM中，将连续体离散成一系列物质点集，其密度可以写成：

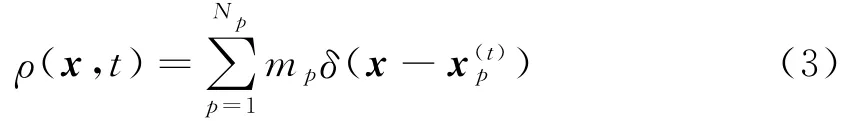
物质点法中需要布置欧拉网格覆盖求解域，同有限元法类似，背景网格单元内的场变量可表示为：

式中：g（x，t）为任意场变量，可代表速度、加速度和试函数等；Ni（x）为单元形函数。

利用式（3）和式（4），式（2）可写成如下形式：

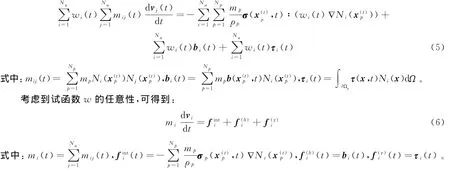
在球对称形式下，各物理量只是r的函数，与θ和φ无关，应力张量有如下形式：

在球对称形式下，其内力向量只有沿径向的分量，其径向分量为：

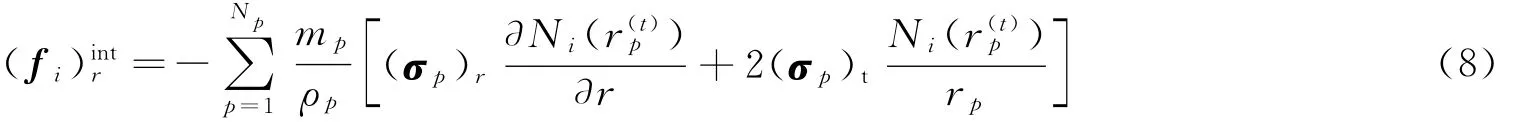
采用显式差分格式求解式（6），从而得到节点的更新速度：

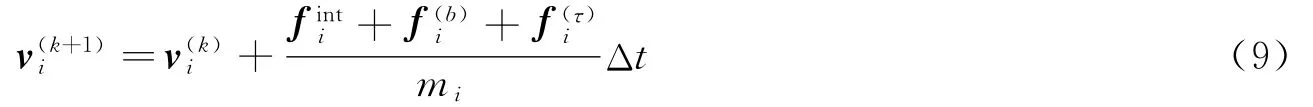
式中：上标k和k＋1分别代表上一时间步和更新后的时间步。

利用更新后的节点速度更新物质点的位置和速度：

在球对称形式下，物质点的应变增量只与r有关，可以写成：

得到物质点的应变增量后，通过材料的本构方程便可完成物质点的应力以及其他内部变量的更新。在球对称形式下的应力更新过程与笛卡尔坐标系下的计算过程没有太大的区别。

2 水下爆炸的数值模拟

2.1 数学模型描述

对球形TNT装药在水下自由场中的爆炸过程进行了数值模拟。为了简化理论分析，忽略水下爆炸过程中热传导和黏性的影响。水下爆炸过程可由下列一组欧拉方程和恰当的状态方程来模拟：

式中：ρ、e、p、v和t分别为密度、内能、压力、速度矢量和时间。

式（13）中前3个方程分别描述了质量守恒、动量守恒和能量守恒，最后一个方程代表不同材料的状态方程。状态方程用来定义固体或流体在不同状态下的压力和密度以及比内能之间的函数关系。正确选取状态方程以及对状态方程中的参数设定合适的数值对于计算结果至关重要。

本文中，对水采用多项式状态方程：

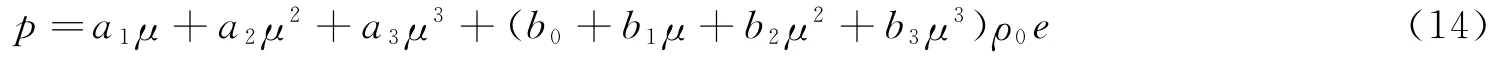
对TNT炸药采用JWL状态方程：

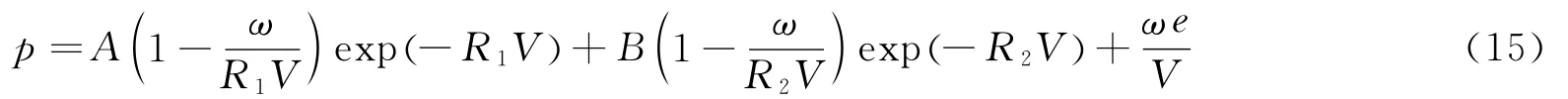
在求解水下爆炸冲击问题时，冲击波将导致压力、密度、质点速度和能量等在波阵面前后发生突变（跳跃），这种不连续性给运动微分方程的求解带来了较大的困难。为了解决此问题，引入了人工黏性的概念。人工黏性将应力波的强间断面模糊成一个在相当狭窄的过渡区域内连续变化的波阵面，从而给工程应用带来极大的方便［16］。

本文中采用线性形式和二次形式相结合的人工黏性形式：

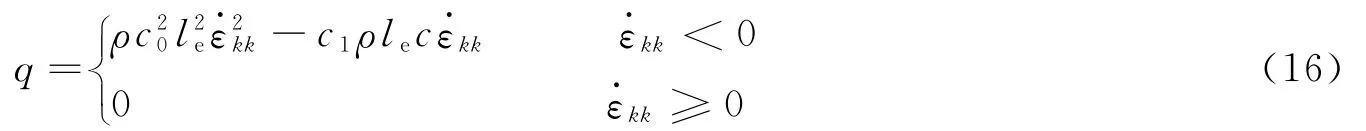
式中：c0和c1为人工黏性系数；le为特征长度，在物质点法中，取背景网格最小尺寸；ρ为现时构形密度为体积应变率，c为材料声速。

2.2 计算结果与分析

图2 一维球对称计算模型Fig.2 One－dimensional spherically－symmetric model

计算模型如图2所示，球形TNT装药半径为0.1m，水域半径为5m，离散网格尺寸为0.01m，每个网格放置2个物质点，总粒子数为1000。

图3给出了分别采用Cole经验公式、MPM和DYNA程序得到的水中不同位置处冲击波压力峰值，图中a为炸药半径，R为观察点到起爆中心的距离。从图3可以看出压力峰值都随水中冲击波的传播而逐渐减小，而且都呈指数形式衰减，这符合水下爆炸冲击波的基本规律。在离起爆中心较近的地方，采用MPM和DYNA计算的结果与采用Cole经验公式计算结果相对误差较小，但随着离起爆点距离的增加，相对误差有增大的趋势。与采用Cole经验公式计算的结果相比，采用MPM和DYNA计算的压力峰值衰减更快。这主要是因为MPM和DYNA均采用理想化的计算模型，忽略了水的黏性、密度不均匀性以及重力等影响因素，而实际的水下爆炸过程很复杂，Cole经验公式是由大量的实验数据拟合得到的，所以采用MPM和DYNA计算的结果与采用Cole经验公式计算的结果之间的误差是合理的。不同爆距处，采用MPM和DYNA计算结果与采用Cole经验公式计算结果之间的相对误差εr，MPM和εr，DYNA见表1。

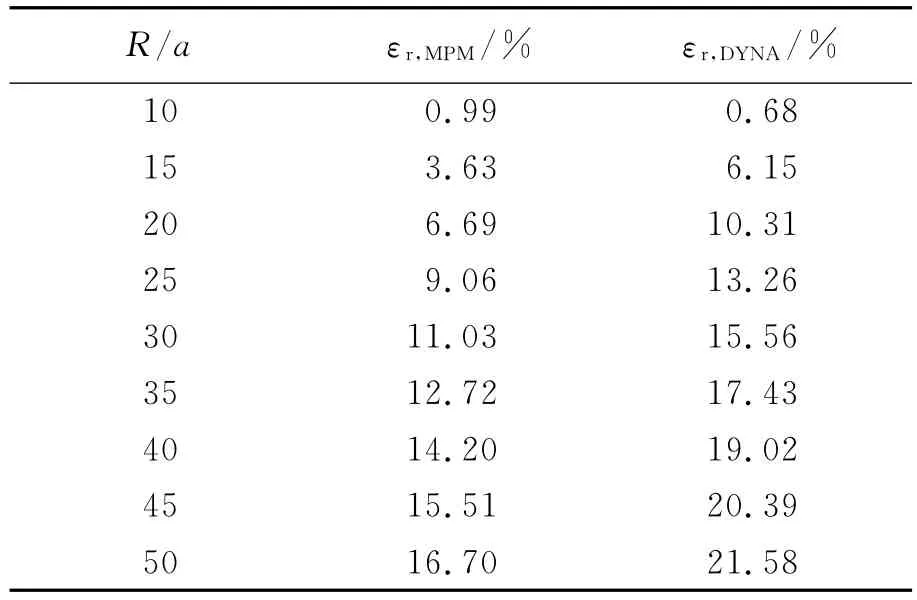
表1 不同爆距处，采用MPM和DYNA计算的结果与采用Cole经验公式计算的结果之间的相对误差Table1 Relative errors between calculated results by MPM and DYNA and ones by Cole formula at different locations

图4给出了几个典型时刻水下冲击波压力沿径向的分布曲线。从图4可以看出，采用MPM计算得到的冲击波前沿位置与冲击波峰值大小与采用DYNA的计算结果吻合较好，冲击波沿径向以近似指数衰减的阶梯式增长。在炸药爆轰产物与水介质的交界面附近，有一定的数值振荡产生，这是由爆轰产物与水介质的不均一性导致的，但数值振荡与冲击波大小相比是可以接受的。随着冲击波背离起爆中心向外传播，其波形被不断拉宽，且峰值具有明显的衰减现象。

本算例如果采用三维模型进行计算，并假设采用与一维球对称模型相同的网格离散精度，即在0.01m×0.01m×0.01m的离散网格内放置8个物质点，即使采用1／8模型，离散物质点总数也将达到1000×1000×1000。三维模型计算规模远大于离散物质点总数为1000的一维球对称计算模型，使数据的计算量和存储量变得很庞大，很难处理，需在大型并行机上完成计算。虽然通过降低网格离散精度，可以在一定程度上减小三维模型的计算规模，但即使采用0.1m×0.1m×0.1m网格尺寸进行离散，其物质点总数为100×100×100与一维球对称模型相比，其计算规模仍很巨大。与三维计算模型相比，一维球对称模型在保证网格离散精度的同时可以有效减小计算规模。

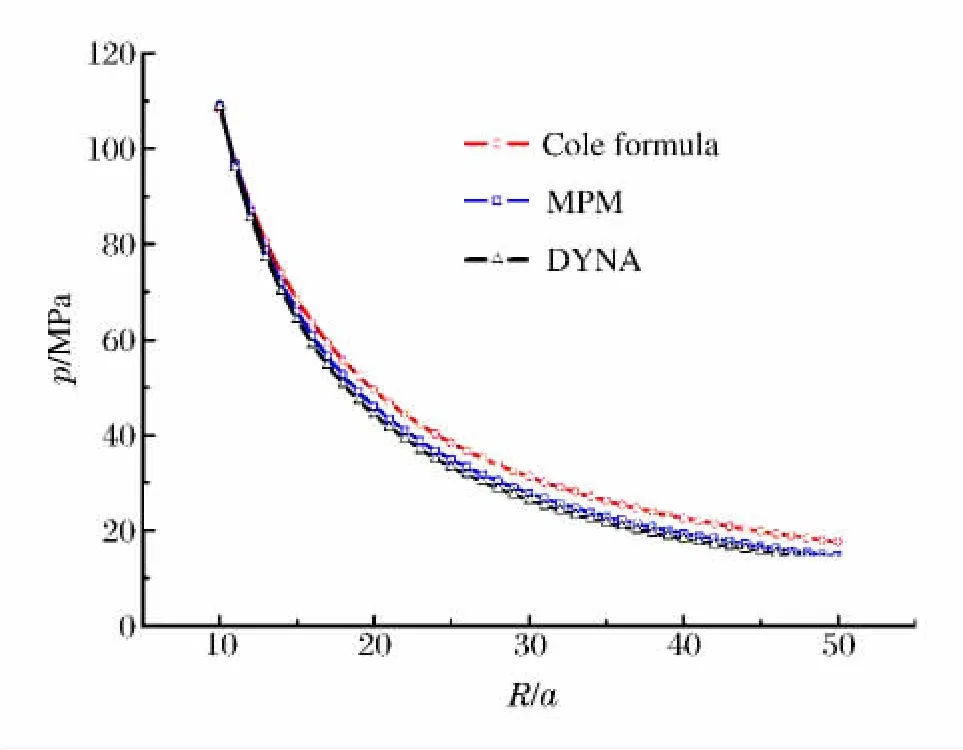
图3 压力峰值沿径向的分布曲线Fig.3 Pressure peak distribution along radial direction

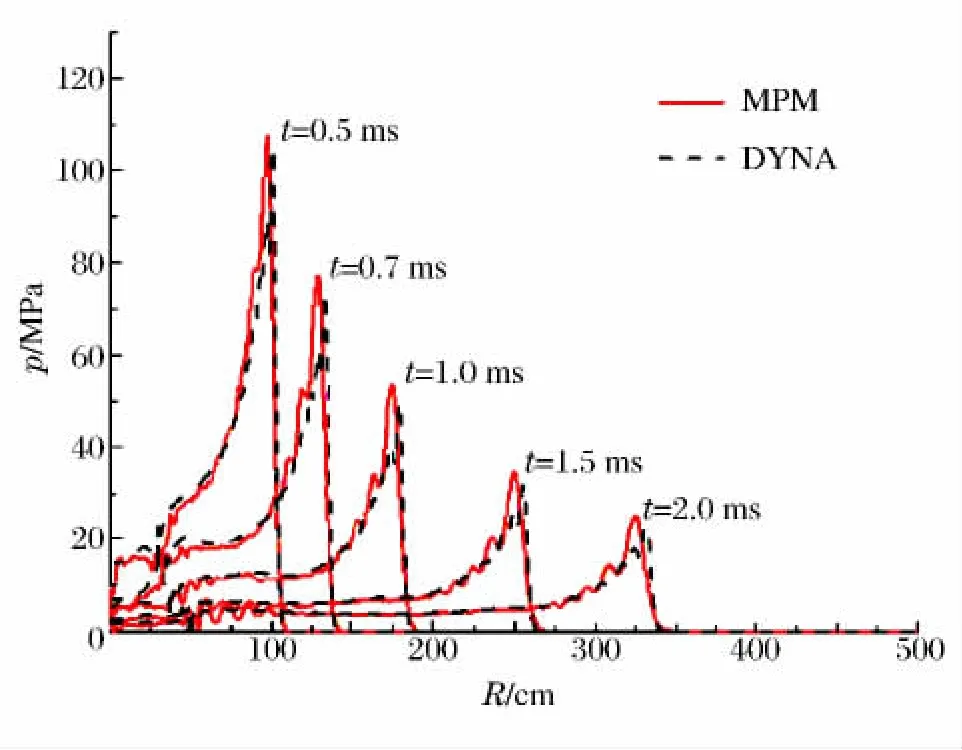
图4 典型时刻的压力分布曲线Fig.4 Pressure distribution curves at typical times

2.3 基于物质点法的重映射算法

重映射计算需要用到球坐标系与笛卡尔坐标系的转换矩阵，2个坐标系下基矢存在如下关系：

式中：er、eθ和eφ为球坐标系下单位基矢量，ex、ey和ez为笛卡尔坐标系下单位基矢量，R为转换矩阵。

对于矢量a，如速度、加速度和力等，在笛卡尔坐标系与球坐标系间有如下的转换关系：

对于张量B，如应力张量，在笛卡尔坐标系与球坐标系间有如下的转换关系：

基于物质点法的重映射计算，采用如下的求解步骤：

（1）将球对称形式下物质点携带的内部变量，如密度、压力和能量等映射到球对称的网格节点上；

（2）通过式（4）得到球坐标系下场变量的空间分布；

（3）通过式（18）和（19）将场变量转换到笛卡尔坐标系下；

（4）将笛卡尔坐标系下场变量的分布空间作为一个连续体，采用物质点进行离散，其中在一维球对称形式下的物质分界点变成三维空间中的物质分界面。

以上4步便完成了将一维球对称计算结果到三维笛卡尔坐标系下的映射计算过程。

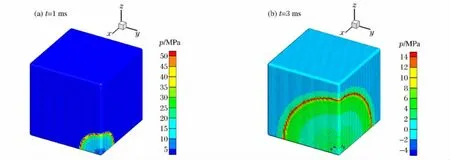
图5 映射后的三维计算模型Fig.5 Mapping to the three－dimensional computational model

图5给出了算例中t＝1ms和t＝3ms时刻计算结果映射后的三维计算模型。一维球对称形式下的计算结果将作为初值赋值给三维模型中离散的物质点，以便在三维空间中继续完成结构冲击响应的计算。为了便于观察，图中显示的是1／8模型。

3 结 论

针对求解三维远场水下爆炸冲击响应问题，提出了一维球对称形式物质点法，并进行了数值模拟验证，取得了如下结论：

（1）对比Cole公式、DYNA和一维球对称形式物质点法计算结果，在起爆中心附近MPM、DYNA和Cole公式计算结果间相对误差较小，随起爆点距离增加，相对误差有增大趋势，但仍在误差允许范围之内。因此，采用一维球对称形式物质点法能够较好模拟水下爆炸过程；

（2）在爆炸模拟过程中，通过重映射算法，将一维球对称计算结果映射到三维计算模型中，避免了计算资源在冲击波传播过程计算上的消耗，显著降低了三维远场水下爆炸冲击响应求解复杂度，具有较高的工程实用价值。

［1］师华强，汪玉，宗智，等.近水面水下爆炸二维Level＿set数值模拟［J］.计算力学学报，2010，27（3）：409－414.Shi Hua－qiang，Wang Yu，Zong Zhi，et al.2Dnumerical simulation of underwater explosion near free surface based on Level＿set method［J］.Chinese Journal of Computational Mechanics，2010，27（3）：409－414.

［2］李健，荣吉利，项大林.装药量及水深对水下爆炸气泡动态特性的影响［J］.爆炸与冲击，2010，30（4）：324－348.Li Jian，Rong Ji－li，Xiang Da－lin.Effects of charge mass and water depth on dynamic behaviors of an underwater explosion bubble［J］.Explosion and Shock Waves，2010，30（4）：324－348.

［3］梁龙河，曹菊珍，袁仙春.水下爆炸特性的二维数值模拟研究［J］，高压物理学报，2004，18（3）：203－208.Liang Long－he，Cao Ju－zhen，Yuan Xian－chun.2DNumerical simulation of characteristics of underwater explosions［J］.Chinese Journal of High Pressure Physics，2004，18（3）：203－208.

［4］张振华，朱锡，白雪飞.水下爆炸冲击波的数值模拟研究［J］.爆炸与冲击，2004，24（2）：182－188.Zhang Zhen－hua，Zhu Xi，Bai Xue－fei.The study on numerical simulation of underwater blast wave［J］.Explosion and Shock Waves，2004，24（2）：182－188.

［5］强洪夫，王坤鹏，高巍然.基于完全变光滑长度SPH方法的高能炸药爆轰过程数值试验［J］.含能材料，2009，17（1）：27－31.Qiang Hong－fu，Wang Kun－peng，Gao Wei－ran.Numerical simulation of high explosive detonation process using SPH method with fully variable smoothing lengths［J］.Chinese Journal of Energetic Materials，2009，17（1）：27－31.

［6］杨刚，韩旭，龙述尧.应用SPH 方法模拟近水面爆炸［J］.工程力学，2008，25（4）：204－208.Yang Gang，Han Xu，Long Shu－yao.Simulation of underwater explosion near air－water surface by SPH method［J］.Engineering Mechanics，2008，25（4）：204－208.

［7］Liu G R，Liu M B，Zong Z，et al.Numerical simulation of underwater explosion by SPH［C］∥Atluri S N，Brust F W.Proceedings of the Advances in Computational Engineering ＆ Sciences.US：Tech Science Press，2000：1475－1480.

［8］Liu M B，Liu G R，Lam K Y，et al.Smoothed particle hydrodynamics for numerical simulation of underwater explosions［J］.Computational Mechanics，2003，30（2）：106－118.

［9］马上，张雄.聚能装药射流形成的自适应物质点法模拟［J］.固体力学学报，2009，30（5）：504－508.Ma Shang，Zhang Xiong.Adaptive material point method for shaped charge jet formation［J］.Chinese Journal of Solid Mechanics，2009，30（5）：504－508.

［10］张忠，陈卫东，杨文淼.非均质固体炸药冲击起爆的物质点法［J］.爆炸与冲击，2011，31（1）：25－30.Zhang Zhong，Chen Wei－dong，Yang Wen－miao.The material point method for shock－to－detonation transition of heterogeneous solid explosive［J］.Explosion and Shock Waves，2011，31（1）：25－30.

［11］张忠，陈卫东.基于物质点法的超高速碰撞问题研究［J］.哈尔滨工程大学学报，2010，31（10）：1312－1316.Zhang Zhong，Chen Wei－dong.Solving hypervelocity impact problems with the material point method［J］.Journal of Harbin Engineering University，2010，31（10）：1312－1316.

［12］王宇新，陈震，张洪武，等.多层抗爆结构冲击响应无网格 MPM 法分析［J］.工程力学，2007，24（12）：186－192.Wang Yu－xin，Chen Zhen，Zhang Hong－wu，et al.Response of multi－layered structure due to impact load using material point method［J］.Engineering Mechanics，2007，24（12）：186－192.

［13］Sulsky D，Chen Z，Schreyer H L.A particle method for history－dependent materials［J］.Computer Methods in Applied Mechanics and Engineering，1994，118（1／2）：179－196.

［14］Tham C Y.Numerical simulation on the interaction of blast waves with a series of aluminum cylinders at near－field［J］.International Journal of Impact Engineering，2009，36（1）：122－131.

［15］Cole R H.Underwater explosion［M］.New Jersey：LISA，Princeton University Press，1948：31－70.

［16］张雄，王天舒.计算动力学［M］.北京：清华大学出版社，2007：273－274.