超高速水下航行器纵向运动稳定性分析

邹启明, 王改娣



超高速水下航行器纵向运动稳定性分析

邹启明, 王改娣

(中国船舶重工集团公司第705研究所, 陕西西安, 710075)

为了进一步研究超高速航行器空化减阻问题, 建立了空化状态下超高速水下航行器纵向运动数学模型, 对该航行器在巡航段平衡状态下受扰动时的攻角和俯仰角速度的阶跃响应进行了分析,并通过根轨迹法分析了运动的稳定性。分析结果表明, 通过给定平衡攻角和平衡舵角, 航行器能够呈现一定的静稳定性, 该特性有利于以直航弹道为主的超高速水下航行器保持超空泡稳定。

超高速水下航行器; 纵向运动; 阶跃响应; 根轨迹法; 稳定性

0 引言

超高速水下航行器利用超空化减阻的原理, 可使其所受的流体阻力减小1~2个数量级, 从而大大提高航行速度, 达到快速攻击目标的目的。超高速水下航行器在不同的运动阶段和不同状态下, 流场发生了根本的变化, 即从单相流变为多相流, 致使航行器的受力状态也发生了变化。与常规航行器相比, 其运动特性也表现出其独有的特点。本文主要以超高速水下航行器在巡航段高速运动状态下的雷体特性为例, 建立纵向的运动方程, 然后对定常运动模型进行简化, 得到描述雷体特性的数学模型, 研究和分析超高速水下航行器纵向运动的稳定性。

1 纵向运动数学模型

在建立纵向运动数学模型中, 对航行器在巡航段的受力情况作如下假设:

1) 速度为常值, 空泡数为恒定值, 空泡稳定闭合在航行器上, 滑行力作用点不变;

2) 航行器在巡航段的质量、质心及转动惯量不变;

3) 由于沾湿部分很小, 忽略流体动力附加质量和浮力, 不考虑尾舵作用。

根据以上假设, 利用刚体的动力学和运动学建模方法, 得到在以质心为原点的航行器坐标系中的纵向运动方程简化形式

通过数值计算和试验结果得到流体系数以及位置导数, 其中式(1)中的舵升力可以表示为, 其中,为升力系数、为空化数、为海水密度、为攻角、为顶端舵角、空化器面积; 滑行力可以表示为, 其中,为航行器的特征面积,为零顶端舵偏时滑行力对攻角的位置导数,为零攻角时滑行力对顶端舵角的位置导数。

由于航行器在巡航段运动时,,为小量变化, 可假定,。

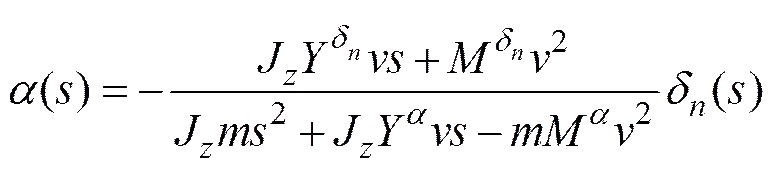
(3)

特征方程为

2 纵向运动分析

2.1 时频特性分析

以超高速水下航行器试验模型为例, 进行超高速水下航行器巡航段工况下稳定性分析。

在定常直线运动过程中, 航行器具有纵向稳定性的充分和必要条件是, 特征方程复根的所有实部以及实根均为负数。同时, 自由运动衰减时间越短, 航行器的稳定性就越好, 衰减时间主要取决于绝对值较小的一个特征根。通过代入有关试验模型参数于式(4)中进行计算, 可知该特征根为1对实部小于零的共轭复数, 这表明航行器的自由运动为一振荡衰减的运动, 即该2阶系统是稳定的, 扰动后运动参数的变化是收敛的。

1) 攻角时频特性分析

由攻角传递函数的表达式可知, 系统拥有1对负实部共轭极点和1个负实数零点。攻角根轨迹如图1所示, 攻角的单位阶跃响应特性曲线如图2所示。

由图1可知, 攻角根轨迹始终在S左半平面内, 系统保持稳定。由图2可知, 曲线为2阶欠阻尼振荡特性, 超调量为17.8%, 阻尼系数。分析超调量偏大的原因, 是由于航行器表面大部分为超空泡所包裹, 附加转动惯量很小, 造成系统阻尼系数较小所致。通常情况下阻尼系数取0.4～0.8, 这时超调量(1.5%～25.4%)适度, 调节时间较短。超高速水下航行器攻角不宜过大, 否则, 包裹航行器的超空泡将会破灭, 造成航行器不稳定运动。因此, 要保持航行器在超空泡中稳定航行, 必须充分考虑攻角的超调对航行器运动稳定性及超空泡稳定带来的影响。

2) 俯仰角速度时频特性分析

由俯仰角速度传递函数的表达式可知, 系统除拥有1对负实部共轭极点外, 还有1个负实数零点。俯仰角速度根轨迹如图3所示, 俯仰角速度单位阶跃响应特性曲线如图4所示, 俯仰角速度频率特性曲线如图5所示。

由图3可知, 俯仰角根轨迹始终在S左半平面内, 系统可保持稳定。图4的俯仰角速度单位阶跃响应特性分析与攻角响应特性类似。由图5可知, 对数幅频特性能以－20 dB/dec的斜率通过截止频率, 幅值裕度和相角裕度都较充裕。

2.2 稳定性分析

2.2.1 计算平衡攻角和平衡舵角

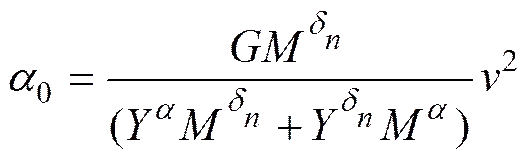
(6)

(7)

2.2.2 静稳定性分析

根据式(7)对超高速水下航行器的静态稳定性做如下分析。

3 结束语

本文建立了巡航段典型工况下的超高速水下航行器纵向运动方程, 通过静稳定性分析和时频特性分析法分析其运动的动态特性, 并计算出平衡攻角和平衡舵角。从分析结果来看, 在巡航段运动时, 超高速水下航行器将呈现一定的静稳定性, 该特性对以直航弹道为主的超高速水下航行器保持超空泡的稳定是有利的。

[1] Savchenko Y N. Supercavitation-problems and Perspectives[C]//Fourth International Symposium on Cavitation. Califormia, 2001.

[2] Logvinovich G V. Some Problems in Planning and Cavitation[M]. Kyiv Trudy TsAGI, 1980.

[3] Anukul Goel. Robust Control of Supercavitating Vehicles in the Presence of Dynamic and Uncertain Cavity[D]. USA: University of Florida, 2005.

[4] Paryshev E V. Mathematical Modeling of Unsteady Cavity Flows[C]//Proceedings of Fifth International Symposium on Cavitation. Osaka, Japan, 2003.

[5] 詹致祥, 陈景熙. 鱼雷航行力学[M]. 西安: 西北工业大学出版社, 1990.

[6] 徐德民. 鱼雷自动控制系统[M]. 西安: 西北工业大学出版社, 2001.

[7] 胡寿松. 自动控制原理[M]. 北京: 国防工业出版社, 1998.

(责任编辑: 陈 曦)

Analysis on Motion Stability of High Speed Underwater Vehicle in Longitudinal Plane

ZOU Qi-ming, WANG Gai-di

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)

In order to study cavitation drag reduction of a high speed underwater vehicle, we establish a longitudinal motion model of the vehicle in supercavitation condition, analyze the step responses of attack angle and pitch angular velocity of the vehicle under turbulence in the balance state of cruise phase, and also analyze the motion stability through the root locus method. The results show that the vehicle can exhibit static stabilization under given balanceable attack angle and rudder angle, which is beneficial to keeping stability of a high speed underwater vehicle with straight running trajectory.

high speed underwater vehicle;longitudinal motion; step response; root locus; stability

TJ630.1;TP13

A

1673-1948(2013)06-0406-04

2013-05-06;

2013-07-04.

邹启明( 1979-) , 男, 在读硕士, 主要从事水下航行器控制仿真研究.