基于层次分析法的国家助学金多级模糊综合评价

耿悦敏

基于层次分析法的国家助学金多级模糊综合评价

耿悦敏

国家助学金的评定受到诸多因素影响，加之评定条件本身属于模糊概念，造成一定程度的主观因素过强、信息不对称。为客观、公正、合理、规范地对申请国家助学金的学生进行评价，本文运用模糊系统理论，建立多级模糊综合评价体系，并运用层次分析法确定了评价指标的权重。由于充分考虑了评价指标的模糊因素，很大程度上降低了主观因素的影响，使评定结果更客观公正。

国家助学金；层次分析法；模糊系统；多级模糊综合评价

耿悦敏/广东交通职业技术学院讲师（广东广州 510650）。

一、引言

为体现党和政府对普通本科高校、高等职业学校家庭经济困难学生的关怀，帮助他们顺利完成学业，根据《国务院关于建立健全普通本科高校、高等职业学校和中等职业学校家庭经济困难学生资助政策体系的意见》（国发[2007]13号），决定在高等教育阶段建立起国家助学金等对高校家庭经济困难学生资助政策体系。政策实施五年来，国家助学金的评选出现了一些不容忽视的问题：部分非贫困生挤占助学金名额；获资助的学生也并非都是贫困生；少数贫困生感情受到伤害[1]。分析问题形成的原因，主要在于现有国家助学金评定条件的实际操作性不强，如国家助学金主要用于资助“贫困生”，然而“贫困生”的认定难度却很大。作为评定的重要指标之一，“贫困”本身就属于模糊的概念，加之当前“贫困生”的认定主要采用定性而非定量的方法，造成一定程度的主观因素过强、信息不对称。如何客观、公正、合理、规范地对申请国家助学金的学生进行评价，使国家助学金的发放，既能真正解决贫困学生的实际困难，让品学兼优的贫困生得到切实的资助，又能最大限度地发挥助学金对贫困生的激励和教育作用，已成为现阶段亟待解决的问题。

二、问题分析

国家助学金的设立是为激励普通本科高校、高等职业学校学生勤奋学习，努力进取，在德、智、体、美等方面得到全面发展，体现党和政府对家庭经济困难学生的关怀，帮助他们顺利完成学业而采取的重大举措。其申请条件：（1）热爱社会主义国家，拥护中国共产党的领导；（2）遵守宪法和法律，遵守学校各项规章制度；（3）诚实守信，道德品质优良；（4）勤奋学习，积极上进；（5）家庭经济困难，生活俭朴。由此可见，国家助学金的资助对象是“贫困生”，条件还要求“勤奋学习，积极上进”。但“贫困”、“勤奋”和“积极”本身都属于模糊概念，所谓模糊是指客观事物差异的中间过渡中的“不分明性”或“亦此亦彼性”[2]。 例如“贫困”与“不贫困”、“勤奋”与“不勤奋”、“积极”与“不积极”之间没有绝对分明和固定不变的界限，这些现象就很难用经典的数学方法进行描述。因此，本文利用模糊数学和综合评价的理论与方法，同时运用层次分析法确定评价指标的权重，建立国家助学金多级模糊综合评价体系。

三、评价方法及原理

（一）层次分析法理论

20世纪70年代美国著名运筹学家T·L·Saaty等人提出了一种多目标、多准则的决策方法——层次分析法（Analytic Hierarchy Process,简记AHP）。它能将一些量化困难的定性问题在严格数学运算基础上定量化；将一些定量、定性混杂的问题综合为统一整体进行综合分析。这种方法在解决问题时，可对定性、定量之间转换、综合计算等解决问题过程中人们所作判断的一致性程度等问题进行科学检验[3]。

（二）基于层次分析法的评价指标权重确定[4]

根据影响评价对象的主要因素，建立系统的递阶层次结构以后，需要运用层次分析法确定各评级指标的权重，大体可分为四个步骤进行：

第一，以上一层次某因素为准，它对下一层次诸因素有支配关系，两两比较下一层次诸因素对它的相对重要性，并赋予一定分值，一般采用Saaty教授提出的1-9尺度法，见表1所示。

表1 1-9尺度的含义

第二，由判断矩阵计算被比较元素对于该准则的相对权重。依据判断矩阵求解各层次指标子系统或指标项的相对权重，就是计算判断矩阵最大特征根及其对应的特征向量。以判断矩阵A为例，即由

其中A为判断矩阵；λ为特征根；ω为特征向量，解出λmax及对应的ω。将λmax所对应的最大特征向量归一化，就得到下一层相对于上一层的相对重要性的权重值。

第三，一致性检验。用判断矩阵最大特征根以外其余特征根的负平均值，作为度量建立判断矩阵过程中所作的所有两两比较判断偏离一致性程度的指标CI（Consistency Index）。

其中n为判断矩阵阶数；λmax为判断矩阵最大特征根。判断矩阵一致性程度越高，CI值越小。当CI=0时，判断矩阵达到完全一致。

Saaty又引入随机一致性指标RI来修正CI，将它的一致性指标CI与同阶的随机一致性指标RI之比称为一致性比率CR，当CR＜0.1时认为A的不一致程度在允许范围内，可用其特征向量作为权向量。否则要重新进行成对比较，对A加以调整。

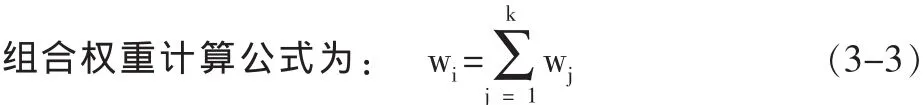
第四，计算各层因素对系统的组合权重，并进行排序其中wij为第i个指标第j层的权重值：k为总层数。

每个判断矩阵一致性检验通过并不等于整个递阶层次结构所做判断具有整体满意的一致性。因此还要进行整体一致性检验。

（三）多级模糊综合评价方法原理

高等院校国家助学金的评定受诸多因素的影响，是一个多层次、多因素的综合评价问题，需要全面地反映家庭经济困难学生的实际情况，有很多指标很难用经典的数学进行分析，所以本文选择多级模糊综合评价法建模。

多级模糊综合评价的基本步骤[5]：

1.给出被评价对象集合 X={x1，x2，x3,…xi}；

2.确定因素集（即评价指标体系）U={u1，u2，u3,…un}，国家助学金评定考虑的因素很多，将U按各属性分解成S个子集：Ui={ui1，ui2，ui3,…uin}（i=1,2,…s），且满足条件：

3.建立评语集 V={v1，v2，v3,…vm}；

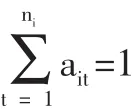
四、模型建立

（一）国家助学金评价指标体系的构建

本评价指标体系的构建以现行国家助学金评定条件为依据，同时遵循以下原则[6]：①导向性原则；②全面性原则；③过程性评价与终结性评价相结合原则；④个性化原则；⑤可操作性原则，同时结合实际评比中容易出现和遗漏的问题，主要从四个方面构建国家助学金综合评价指标体系，如表2所示（表中权重由表4评价指标权重的确定算得）。

表2 国家助学金综合评定指标

（二）建立评语集V

V={v1（很好），v2（较好），v3（一般），v4（不好）}，其中，vi（i=1，2，3，4）表示第 i个评价等级.用专家咨询法确定 100～90 分为优秀，89～80 为良好，79～70 为一般，69～60 为较差。 将评语集的等级用1分制数量化，得到评价等级向量V'={1，0.8，0.5，0.3}。

（三）评价指标权重的确定

采用层次分析法确定权重，首先构造比较判断矩阵。由专家根据1-9尺度法将指标进行两两比较，得出判断矩阵；其次对判断矩阵进行运算和正规化处理；最后对判断矩阵进行一致性检验。结果如表3所示。

表3U 层对目标层A的判断矩阵及权重计算

运用相同的方法进一步对整个指标体系进行计算，得到了如下的指标体系的判断矩阵和权重计算，见表4，5，6,7。

表4u 层对目标层U1层的判断矩阵和权重计算

表5u 层对目标层U2层的判断矩阵和权重计算

表6u 层对目标层U3层的判断矩阵和权重计算

表7u 层对目标层U4层的判断矩阵和权重计算

（四）模糊评价矩阵的建立

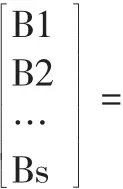
本模型由评定小组根据评判集对申请人进行评判，由评判结果构造出每个因素的评判和模糊矩阵。如记第i个二级因素的评判为（ri1，ri2，ri3，ri4）（i=1，2，3，4），则相应一级因素的模糊评价矩阵为

（五）多级模糊综合评价

一级模糊综合评价：Bi=Ai×Ri，（i=1，2，3， 4）。

二级模糊综合评价：B=A×R，

为方便排序比较，将模糊综合评价值转化为一个确定的标量值:b=V'×BT。

（六）评价结果处理及应用

以本班申请国家助学金的同学甲为例，通过评定小组的评价，运用上述方法建立的模糊评价综合评价体系进行综合评价，得到如下结果：

一级模糊综合评价：B1=A1×R1=[0.827 0.173 0 0]，B2=A2×R2=[0.623 0.273 0.104 0]，B3=A3×R3=[0.606 0.364 0.03 0]，B4=A4×R4=[0.667 0.23 0.103 0]。

二级模糊综合评价：B=A×E=[0.68 0.25 0.07 0]。

对应评价等级向量 V'={1，0.8，0.5，0.3}， 可将模糊综合评价值转化为一个确定的标量值:b=V'×BT=[1 0.8 0.5 0.3]×[0.68 0.28 0.07 0]T=0.915,

即该学生的模糊综合评价值为0.915。

重复上述步骤即可得出各参评学生的模糊综合评价值，从高到低依次排序，即可选出国家助学金的合适人选。

五、模型的分析与改进

多级模糊综合评价模型充分考虑了评价指标的模糊因素，运用模糊数学的方法对一些带有模糊性的条件给出定量分析，很大程度上降低了主观因素的影响，关于各因素的权重主要是依据实际背景主观上给定的，实际操作时可以根据侧重点适当调整，不影响整体效果，并且本模型中详细地分析了各因素之间的关系，利用AHP方法通过两两比较矩阵确定权向量，使评定结果更客观公正。因此，本模型还可应用到奖学金、三好学生等各类评比项目。

本模型仍需改进之处：利用AHP方法通过两两比较矩阵确定权向量时，结果虽然更客观，但需要大量的计算，如果单纯依赖人工完成，其工作量之大可想而知，因此，未来可以考虑利用计算机辅助建立起综合测评系统，操作人员只需将评定小组给出的评定结果输入计算机就可完成综合评价的全过程,从而使国家助学金的评定体系更加完善，评定结果更加科学、公正。

：

[1]郭昕，田辉玉.国家助学金评选面临的问题与对策[J].教育与经济，2011：（4）：38-40

[2]刘焕彬等.数学模型与实验[M].北京：科学出版社，2008：157-182

[3]万远英，尹德志．大学生综合素质层次分析评价体系及其数学模型[J]．西南民族大学学报（人文社科版），2003，24（12）：191-193

[4]夏怡新．构建高校学生综合素质评价体系的思考[J]．教育探索，2003（8）：53-5

[5]谢季坚，刘承平.模糊数学方法及其应用[M].武汉：华中科技大学出版社，2000：197-215

[6]胡庆宇.基于层次分析法的大学生综合素质多级模糊评价[D].保定：华北电力大学，2010：33-40

O029

A

1671-6531（2013）16-0134-03

责任编辑：姚 旺