基于轮廓线的任意形体三维重建

钱苏斌

(盐城师范学院信息科学与技术学院，江苏盐城 224002)

基于轮廓线的任意形体三维重建

钱苏斌

(盐城师范学院信息科学与技术学院，江苏盐城 224002)

由二维灰度图像恢复形体的三维形状已经成为计算机视觉领域的一个研究热点.对该问题进行了深入的研究，提出了一种基于单幅图像，利用轮廓线进行形体三维重构的方法.该方法从一幅二维灰度图像的断层剖面中使用行扫描线法提取带有孔洞的轮廓线，并且根据一定的准则对其进行分层处理，采用曲率法对各相邻层轮廓线中的分层轮廓线进行匹配，结合最小对角线优化策略完成三角面片拼接，最终实现任意形体表面的三维重建.实验证明，该方法可以根据形体的二维灰度图像方便有效地重建出其三维形状.

任意形体;三维重建;行扫描线;分层轮廓线;三角面片拼接

0 引言

近年来，三维重建技术逐步成为计算机视觉领域的一个研究热点.客观世界是一个三维的空间，而现有的图像采集装置所获取的图像(如数码相机所拍摄的照片)是二维的，在二维图像中往往又含有某种形式的三维结构信息，如形体边与边的平行或垂直关系、形体本身的特殊几何对称性［1］，对这样的形体进行重建只需要一幅图像就可以构造出物体的模型.而另外一些形体本身结构构成中各几何要素间并不具备明显的结构信息，对于这样一些形体，其二维图像上的轮廓线便成为理解其几何形状的一个重要线索.基于轮廓线的三维重建，传统方法是将每层图像的轮廓提取出来，然后以轮廓上的点为顶点进行三角面片的连接［2-4］，该方法对于结构简单的形体效果比较好，对于结构较为复杂的形体而言，相邻两层轮廓线的对应关系较难确定.针对上述问题，有报道提出，首先对轮廓线进行凹凸性层次分析，然后将相邻轮廓线从外到内依次逐层拼接，从而构造一个三角化的物体表面［5］，但该算法在进行凹凸性层次分析时涉及到的数据量较大.在此基础上，本研究提出了一种基于轮廓线的改进算法:使用行扫描线法对带有孔洞的断层剖面提取轮廓线，并且依照一定的规则对轮廓线进行分层处理，然后采用曲率法对各相邻层轮廓线中的分层轮廓线进行匹配.该方法可以快速、高效完成形体三维重建.

1 基于轮廓线的任意形体表面重建

1.1 轮廓线提取

轮廓线是实体与某一特定平面的交线，它在相当大的程度上反映了实体的形状特征.在进行轮廓线提取之前，首先对原始的断层剖面图像做阈值分割，将目标对象从背景图中分离出来，如图1所示，黑色部分即为形体的断层剖面经过阈值分割处理后得到的目标区域.

图1 断层剖面阈值分割

由于上述目标区域中存在孔洞，而孔洞的边界轮廓也是像素信息发生突变的点，所以轮廓线提取的过程中应当对所提取出来的突变点做分层处理.根据实际需要，以图1为例，按照逆时针的顺序将轮廓线分为3层:layer0、layer1及layer2，一般情况下，将最外层轮廓线定义为layer0层.设置相应的点结构体数组layer0 _point［count］［i］、layer1 _point［count］［i］及layer2 _point［count］［i］，用于存放实体每一断层剖面上的相应分层轮廓线的像素点信息，下标count对应于构成实体的第count层剖面，i对应于第count层剖面上相应分层轮廓线上的第i个像素点.其中，数组变量layer0 _point［count］［i］.x、layer0 _point［count］［i］.y 分别用于存储像素点的二维坐标信息.

1.1.1 轮廓点的确定.

目标区域的像素信息往往与图像其他区域像素信息存在较为明显的区别，它们通常具备以下特点:该点的颜色值及坐标位置是固定的;该点的四邻域中至少存在一个不属于目标区域的像素点.

根据上述特点，使用逐行扫描的方法找到每一行发生像素信息突变的点，这些点即为行扫描线与目标区域边界的交点.如图2(a)、(b)所示的P0、P1及P2即为像素信息发生突变的点，也即轮廓点.

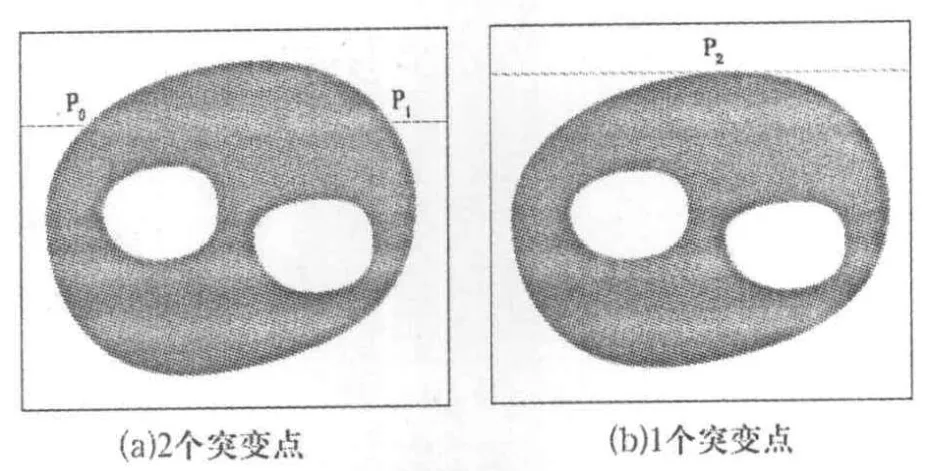
图2 行扫描线与目标区域的交点

一般情况下，行扫描线对上述目标区域进行扫描时，会出现以下几种情形:第一种是不经过孔洞，直接穿过目标区域;第二种是仅仅经过其中1个孔洞(与该孔洞有1个或者2个交点);第三种是同时经过2个孔洞(与这2个孔洞有3个或者4个交点).

1)直接经过目标区域.

图2所示为行扫描线直接经过目标区域，在此前提下一般分为2种情况:一种情况如图2(a)所示，产生2个突变点P0和P1，将P0和P1直接归入layer0层，并且将它们添加进点结构体数组layer0_point中;另一种情况如图2(b)所示，仅产生1个突变点P2，将P2归入layer0层，并将其添加进点结构体数组layer0 _point中.

2)仅经过其中1个孔洞.

图3所示为行扫描线在经过目标区域的时候仅经过其中1个孔洞，在此前提下一般分为2种情况:一种情况如图3(a)所示，仅与该孔洞有1个交点，此时产生3个突变点P0、P1及P2;另一种情况如图3(b)所示，与该孔洞有2个交点，此时产生4个突变点P0、P1、P2及P3.

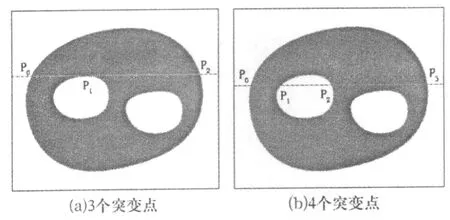
图3 经过其中1个孔洞

3)同时经过2个孔洞.

图4所示为行扫描线在经过目标区域的时候同时经过2个孔洞，在此前提下一般分为2种情况:一种情况如图4(a)所示，与2个孔洞有3个交点，此时产生5个突变点P0、P1、P2、P3及P4;另一种情况如图4(b)所示，与2个孔洞有4个交点，此时产生6个突变点P0、P1、P2、P3、P4及P5.

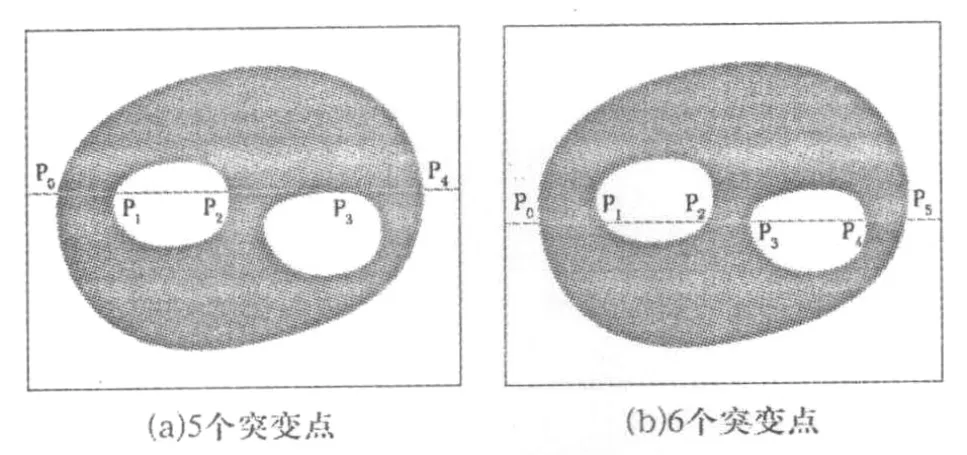
图4 同时经过2个孔洞

在获取每一个突变点的同时，对该突变点做一次特性分析(除最外层的一对突变点).假设某点P(x，y)已经被确定为突变点，进一步判断P'(x+1，y)在二值图上是否为目标区域像素点:如果不是，则P(x，y)是扫描线经过该孔洞时的入点，接下来的扫描中，在该孔洞上必将有1个出点与之配对，即当前扫描线与孔洞有2个交点;如果是，再次判断P'(x-1，y)在二值图上是否为目标区域像素点，如果条件成立，则P(x，y)既是扫描线经过该孔洞时的入点，也是扫描线经过该孔洞时的出点，即当前扫描线与孔洞仅有1个交点.设置数组flag point［k］用于记录每个突变点的特性值，如为前者所述，则特性值设置为“1”，反之则设置为“0”，下标1≤k≤n-1.

此外，具有多个孔洞的断层剖面其轮廓点确定及特性分析可根据实际情况同理推得.

1.1.2 轮廓点的配对.

一般情况下，行扫描线与一条封闭曲线的交点个数至多为2 个.假设轮廓点集为，P={P0，P1，P2，P3，P4…Pi-1，Pi…Pn-2，Pn-1}，对点集中的轮廓点进行两两配对.首先，确定＜P0，Pn-1＞为最外层轮廓线(layer0层)上的轮廓点对，再根据实际情况确定其余孔洞层上的轮廓点对.

1)当轮廓点个数为“1”，即行扫描线仅与断层剖面边界有一个交点P0，则轮廓点对为＜P0，P0＞.

2)当轮廓点个数不为“1”，则依次判断每一个轮廓点的特性值，如果特性值flag _point［k］为“1”，则轮廓点Pi与其之后紧邻的一个轮廓点Pi+1进行配对，构成轮廓点对＜Pi，Pi+1＞，那么下次的特性分析从Pi+2开始;如果特性值flag _point［k］为“0”，则轮廓点Pi与其本身配对，构成轮廓点对＜Pi，Pi＞，那么下次的特性分析从Pi+1开始.

1.1.3 归入层集.

以图2～图4为例，对获取的轮廓点对进行归层操作.

1)当轮廓点个数为“1”时，轮廓点对为＜P0，P0＞，P0直接归入layer0层，并将其添加到数组layer0_point中.

2)当轮廓点个数为“2”时，轮廓点对为＜P0，P1＞，P0、P1直接归入 layer0层，并将其添加到数组layer0 point中.

3)当轮廓点个数为其余值时，＜P0，Pn-1＞直接归入layer0层，设置距离变量dis1和dis2，初值为∞.

设置点结构体变量layer1 binary point、layer2_binary point，分别用于存放轮廓点对的中间点坐标，将分坐标的初值均设为0.假设上一对归入layer1层的轮廓点对为 ＜P2i-5，P2i-4＞，归入 layer2层的轮廓点对为＜P2i-3，P2i-2＞，则上述轮廓点对的中间点坐标分别为，

①如果待归入层的轮廓点对＜P2i+1，P2i+2＞，用 同样方法求得其中间点坐标temp.x、temp.y，则，

当dis1＜dis2时，将 ＜P2i+1，P2i+2＞归入 layer1层，并将P2i+1和P2i+2添加到数组layer1 point中，反之，归入layer2层，并将P2i+1和P2i+2添加到数组layer2 _point中.

②如果现有待归入层的轮廓点对＜P2i+1，P2i+1＞，判断dis1或dis2是否是∞，如果dis1为∞或者两者都为∞，则将P2i+1归为layer1层，如果仅有dis2为∞，则将P2i+1归为layer2层.

图5所示即为形体的某断层剖面使用上述算法获得的轮廓线.

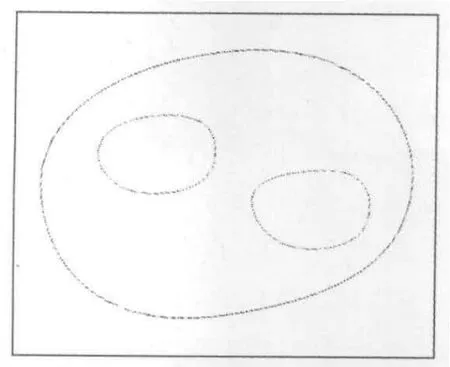
图5 带有孔洞的断层剖面轮廓线

对形体的每一个断层剖面采用上述方法及步骤，即可获取整个形体的有效轮廓线.该算法能够有效提高轮廓线定位精度，降低漏检率，使轮廓线更为细致平滑.

1.2 相邻层轮廓点匹配

将每一个断层剖面中的轮廓线提取了出来，并且按照逆时针顺序对轮廓线进行了分层处理，各层轮廓线上的轮廓点均存放在对应的结构体数组layer0 point［count］［i］、layer1 _point［count］［i］及layer2 _point［count］［i］中.由于通常处理的形体各断层剖面上的轮廓线具有几何形状的相似性，这一特性不仅符合上述过程中的最外层轮廓线，同样也符合内层的孔洞边界.

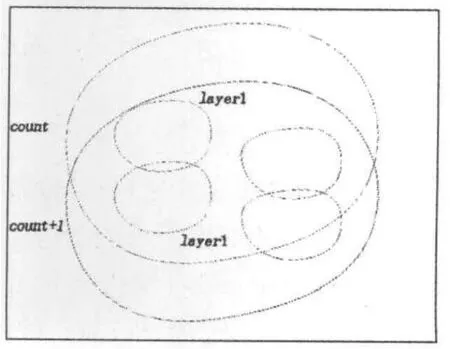
图6 相邻断层剖面轮廓线

图6所示为形体第count层及count+1层断层剖面使用本算法提取出来的分层轮廓线.其中，layer1_point［count］［i］与layer1 _point［count+1］［i］中所存放的分层轮廓线应当具备一定的几何形状相似性.

各分层间的轮廓点匹配的步骤为:将第count+1层断层剖面的layer1层轮廓线作为基层轮廓线，将layer1 _point［count+1］中的点赋予点集P={P1，P2，P3，…，Pm}，将第 count层断层剖面的 layer1 层轮廓线作为待匹配层轮廓线，将layer1 _point［count］中的点赋予点集Q={Q1，Q2，Q3，…，Qn}，其中m≤n.依次从P中取出Pi，从Q中找到一点Qi，采用文献［4］中介绍的曲率角及曲线长度的方法分别计算2点在半径为R的区域内的曲率角，然后再计算它们在曲率角θ(i)和曲线长度s(i)上的误差值.这里，分别设定曲率角和曲线长度的误差值上限为ζ1、ζ2(一般情况下将ζ1设为0.003，ζ2设为3)，当且仅当同时满足条件 θ(i)≤ζ1和s(i)≤ζ2时，Pi和Qi匹配成功，从Q集合中剔除Qi.重复上述过程，直至遍历P中所有的点.对layer0层和layer2层分别使用以上方法进行点的匹配.

1.3 轮廓线分段连接及三角面片拼接

依次连接相邻层已经匹配好的各层轮廓点，将相邻层轮廓线分成几个独立的部分.

如图7 所示，Pi、Pi+1、Qi及Qi+1分别为2 个相邻的layer1层上的点，其中Pi与Qi相匹配，Pi+1与Qi+1相匹配，由这4点构成一个四边形的小面片.

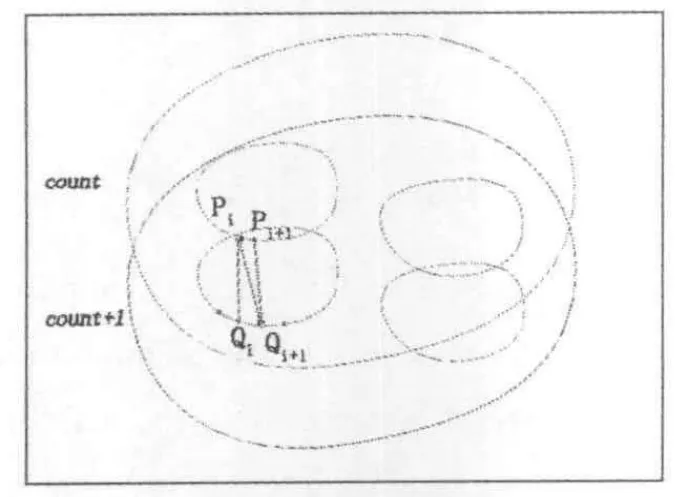
图7 分段拼接

本研究在进行三角面片拼接时，以最小对角线为优化目标［5］.至于对角线是连接Pi、Qi+1，还是Pi+1、Qi可由2跨距的长度来决定，一般采取的原则是取短舍长，这样2个三角面片可同时产生;然后i值增加1，重复上述步骤，使上下两层轮廓线的点同步前进，直至所有点均连接完毕，并返回到起始点，此时一个封闭的表面已经形成.同理，对于各相邻层上的layer0、layer2层均采用上述方法，便可完成全部三角面片的绘制，进而完成整个形体的三维重建.

2 实验结果与结论

2.1 实验结果

在实验中，以OpenGL和VC++6.0为开发工具，采用本研究提出的方法实现了一个基于轮廓线的任意形体三维重建.

图8所示为经过本研究方法重建生成的含有孔洞的三维形体.从实际效果可以看出，重建形体的表面结构合理，基本符合形体本身的轮廓线层次分布.

图8 本研究方法三维重建效果

2.2 结论

本研究提出了一种基于轮廓线的任意形体三维重建方法.该方法使用行扫描线法对带有孔洞的断层剖面提取轮廓线，并且依照一定的规则对轮廓线进行分层处理，然后采用曲率法对各相邻层轮廓线中的分层轮廓线进行匹配，最后以最小对角线为优化目标进行三角面片的拼接，进而得到三维模型.这种方法不仅有效避免了一般形体重建方法所要求的需要较多的几何参数去精确表示曲面形态的缺陷，而且在一定程度上提高了形体重建的精度.

:

［1］钱苏斌.基于二维灰度图像的规则形体三维重建［J］.成都大学学报(自然科学版)，2012，31(3):243-246.

［2］孔令鑫.基于轮廓线的三维重建技术研究［J］.机械与电子，2011，25(10):3-6.

［3］陈敏，鲍旭东.由任意形状轮廓线重建表面的方法研究［J］.计算机工程与应用，2006，41(12):74-76.

［4］王醒策，周明全，刘新宇，等.基于周期性曲率函数的轮廓线匹配技术研究［J］.系统仿真学报，2007，19(17):4045-4048.

［5］袁方，唐杰，武港山，等.一种基于三维Delaunay三角化的曲面重建算法［J］.计算机技术与发展，2011，21(10):14-18.

3D Reconstruction of Arbitrary Shape Object Based on Contour Line

QIAN Subin
(School of Information Science and technology，Yancheng Teachers College，Yancheng 224002，China)

3D reconstruction from the 2D grey image has been a research hotspot in the field of computer vision.This paper makes an intensive study on the hotspot，and proposes a method based on single image and completing 3D reconstruction of arbitrary shape object according to the contour line.The method adopts scanning lines to extract the contour lines with orifices from one 2D grey image’s cross sections，processes them hierarchically according to certain criteria，uses the curvature to match the hierarchical contour lines in adjacent layers，and completes the triangular plane-concatenation according to the shortest diagonal optimization strategy，finally realizes the 3D reconstruction of arbitraty shape object surface.The experimental results indicate that this method could conveniently reconstruct the 3D shape of arbitraty shape object according to its 2D grey image.

arbitraty shape object;3D reconstruction;scanning line;hierarchical contour line;triangular plane-concatenation

TP391.41

A

1004-5422(2013)03-0262-05

2013-08-15.

钱苏斌(1984—)，女，硕士，从事计算机图形学与虚拟现实技术研究.