具次临界扰动项的非线性Hartree方程驻波的存在性

陈 丹，陈 东

(1.成都大学信息科学与技术学院，四川成都 610106;2.成都大学工业制造学院，四川成都 610106)

具次临界扰动项的非线性Hartree方程驻波的存在性

陈 丹1，陈 东2

(1.成都大学信息科学与技术学院，四川成都 610106;2.成都大学工业制造学院，四川成都 610106)

研究了一类具次临界扰动项的非线性Hartree方程驻波解的存在性.根据2个非线性项的特征，分2类情形建立相应的约束变分问题，得到了该类Hartree方程在2种情形下驻波的存在性.

Hartree方程;驻波;存在性

0 引言

本研究考虑如下具非局部非线性项和次临界扰动项的非线性Schrødinger方程，

式中，△ 表示RN上Laplace算子，φ(t，x):R+×RN→C为复值函数，* 是RN上标准卷积.

本研究均定义C为任意正常数.为方便起见，不特别说明的情况下记·dx=∫·dx.

记式(2)的极小子构成的集合为Λ，则对任意u∈Λ，存在Lagrange乘子ζ∈R使得u是如下椭圆方程的解，

这里，φ(t，x)=eiζtu是方程(1)的一个驻波解.由于u是式(2)的极小子时，故eiζtu是u的轨道.

此外，定义Nehari流形，

约束变分问题，

驻波即是形如，φ(t，x)=eiωtu(x)，的方程(1)的解，其中，u是以下不动方程的基态解，

定理1(驻波的存在性) 在以下2种情况下，

方程(1)都存在如下形式，φ(t，x)=eiωtu(x)，的驻波.

1 预备知识

H1(RN)=W1，2(RN)是以 ‖φ‖2=∫(|▽φ|2+|φ|2)dx为范数的标准Sobolev空间.柯西问题(1)的局部适定性如下:

①质量守恒.

②能量守恒.

这里，常数C＞0.

引理3［5］设u*是u的Schwartz对称函数，则对1＜p＜∞有下列4式成立，

引理 4 设 φ0∈H1(RN)，|·|φ0(·)∈L2(RN)，φ(t，x)是柯西问题(1)的解.令J(t):=∫|x|2|φ|2dx，则，

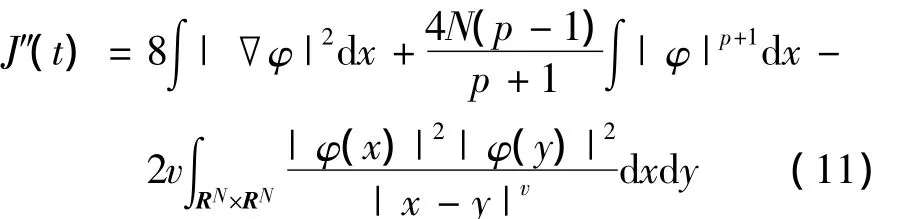
利用文献［6］中的方法，引理3可方便得证.在这里省去证明过程.

2 驻波的存在性

首先考虑定理1的情况①.

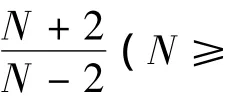
证明 首先定义极小化问题，

式中，Ω-:={u∈H1RN):∫|u|2dx≤M}.

第一步.设{un}n∈N∈H1且，

显然，un≠0.令是un是Schwartz对称函数，由引理3有∈Ω-，且{}是的最小化序列.

由式(14)知，对任意n∈N，{}在H1(RN)是有界的.则存在它的子序列，仍记为{}n∈N，使得，

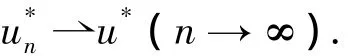
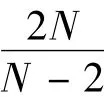
第二步.下证=d*.事实上，需要证明在Ω中可达到.注意到，这里的Ω是Ω-的子集.

①若1＜p＜3.

设uλ(x)=λu(x).如果不成立，则∫|u*|2dx＜M.从而存在λ0∈(1，+∞)，使得，

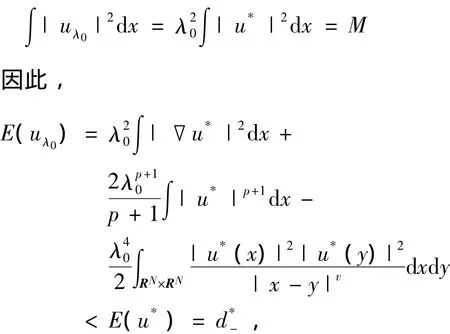
这与的定义矛盾.因此，∫|u*|2dx=M.

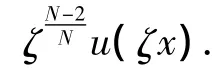
则，E()＜E(u*)=，这与的定义矛盾.因此，

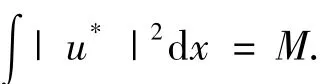
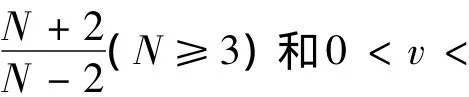
注1 显然，极小化问题的极小子是方程(3)的解.从而由命题2知定理1在条件①下成立.

这部分将讨论定理1在情况②下成立.

引理5d＞0.

证明 由S(u)=0，得到，

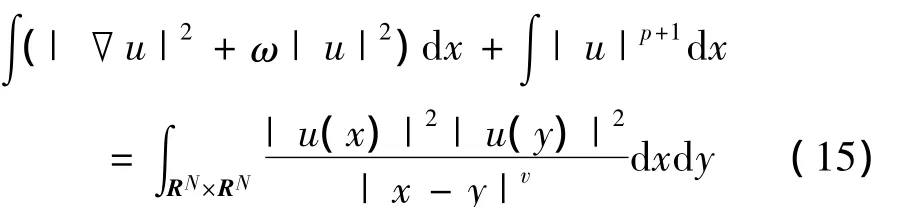
根据引理2有，

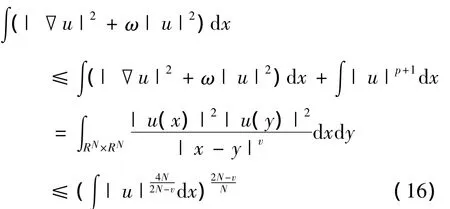
由Sobolev不等式及2≤v＜min{N，4}，得，

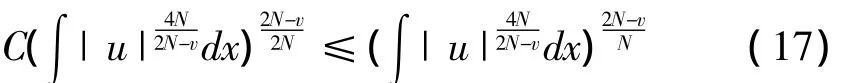
因此，由式(14)有，

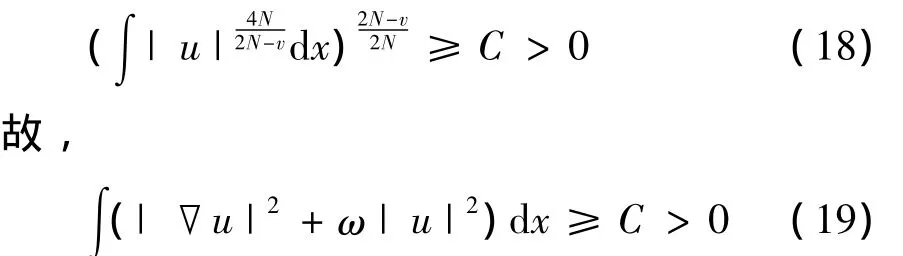
因此，d≥C＞0.

引理6 如果极小化问题(7)在N中达到，则u是式(8)的解.

证明 对任意v∈H1(RN)有，

假设u∈N是I限制在N上的极小子，则由标准极小化理论知，存在Euler-Lagrange乘子Λ∈R使得，

在＜▽I(u)+Λ▽S(u)，u＞=0中，取S(u)=＜▽I(u)，u＞=0，则，

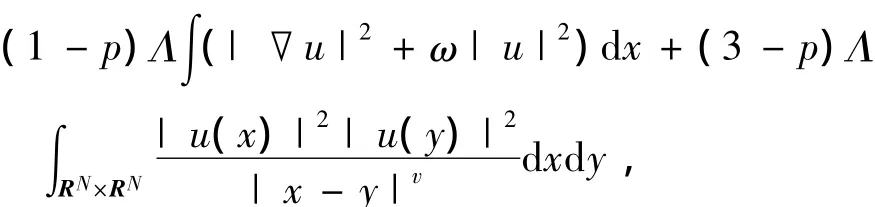
从而，由u≠0，知Λ=0.

为了证明定理1，需要如下引理.定义，

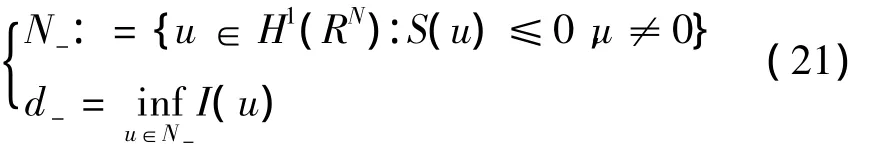
引理7N-，N是非空的.

证明 首先证明N-≠0.任取u∈H1(RN)且u≠0.定义，uλ=(λx)，考虑，

接下来证明，N≠＞，取u∈H1(RN)使得，S(uλ)＜0.当λ=1，S(uλ)＜0;当λ=0，S(uλ)＞0.因此，存在λ*∈(0，1)使得，S(uλ)=0，i.e.∈N.

最后证明定理1在条件②下成立.

证明 为了证明定理1，只需要证明式(8)基态解的存在性.

第一步.考虑约束问题(21)，取d-的极小化序列{un}⊂N-，则，

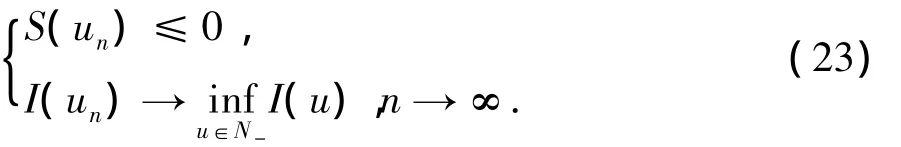
按照引理5的证明方法可得，un≠0.令为un的Schwartz对称函数，由引理3知，

且{}是d-的一个极小化序列.

易知，‖‖H1(RN)在n∈N上是有界的.则存在一个子序列{}(n∈N)使得在H1(RN)中有，⇀u*，n→∞.由紧嵌入引理［7-10］，对于2＜q＜Lq(RN)是紧的，其中)={f(x)∈H1(RN)，f(x)=f(|x|)}.因此，在Lp+1(RN)中有→u*.由H1范数的弱下半连续性知，u*∈N-，且，d-=I(u*).

进而由(23)有，u*≠0.

第二步.下证.

因此，u*∈N-，即u*是I(u)的内部极值点.进而，▽I(u*)=0，即u*是方程(8)的弱解.用u*乘式(8)并在RN上积分，则，

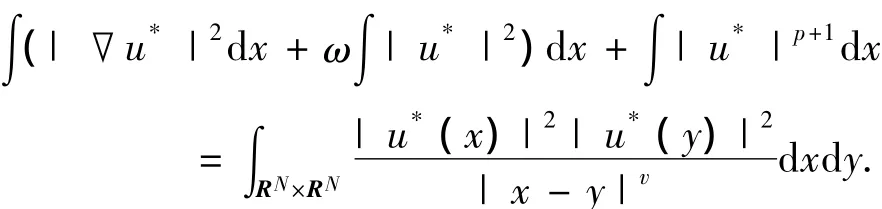
矛盾.

第三步.由第一步和第二步有，

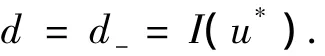
根据引理6知u*是式(8)使得u≠0的解.从而式(8)的基态解的存在性得证.

:

［1］Cazenave T.An introduction to nolinear schrødinger equations［M］.Riode Janeiro:Textos de Metodos Matematicos，1993.

［2］Weinstein M I.Nonlinear schrødinger equations and sharp interpolations estimates［J］.Communications in Mathematical Physics，1983，87(4):567-576.

［3］Reed M，Simon B.Methods of modern mathematical physics:fourier analysis，self-adjointness，vol.II［M］.Academic Press，1975.

［4］Stein E M.Singular integral and differentiability properties of functions［M］.Princeton University Press，1970.

［5］Lieb E，Loss M.Analysis［M］.American Mathematical Society，1996.

［6］Chen J，Guo B.Strong instability of standing waves for a nonlocal Schrødinger equation［J］.Physica D:Nonlinear Phenomena，2007，227(2):142-148.

［7］Kimura Y.Stability and instability of standing waves for the nonlinear Schrodinger equation with the Hartree nonlinearity［D］.Japan:Hokkaido Unviersity，2007.

［8］Rabinowitz P.On a class of nonlinear schrødinger equations［J］.Angewandte Mathematical Physic，1992，43(2):270-291.

［9］Shatah J，Strauss W.Instability of nonlinear bound states［J］.Communications in Mathematical Physics，1985，100(2):173-190.

［10］Strauss W A.Existence of solitary waves in higher dimensions［J］.Communications in Mathematical Physics，1977，55(2):149-164.

Existence of Standing Waves of Nonlinear Hartree Equations with Perturbations

CHEN Dan1，CHEN Dong2

(1.School of Information Science and Technology，Chengdu University，Chengdu 610106，China;2.School of Industrial Manufacturing，Chengdu University，Chengdu 610106，China)

In this paper，we discuss the existence of the standing waves of the nonlinear Hartree equations with perturbations.According to the properties of two nonlinear terms，we establish two constrained variational problems，and then get the existence of the standing waves of these equations in two cases respectively.

Hartree equation;standing waves;existence

O175.29

A

1004-5422(2013)03-0242-05

2013-06-27.

陈 丹(1984—)，女，硕士，从事偏微分方程研究.