基于人工蜂群算法的水平条分法边坡稳定性分析

覃 亮，裴向军，陈曦阳

(1.成都理工大学环境与土木工程学院，四川成都 610059；2.中机三勘岩土工程有限公司，湖北武汉 430030)

基于人工蜂群算法的水平条分法边坡稳定性分析

覃 亮1，裴向军1，陈曦阳2

(1.成都理工大学环境与土木工程学院，四川成都 610059；2.中机三勘岩土工程有限公司，湖北武汉 430030)

根据极限平衡原理，推导出了适合地震作用下成层状岩土体边坡稳定性计算的水平条分法公式，并将人工蜂群算法用于水平条分法边坡最危险滑动面搜索，提出了基于人工蜂群算法的边坡稳定性的极限平衡水平条分法.算例分析表明，该方法能快速搜索到全局最优解，稳定性计算结果是可靠的，适合成层状岩土体边坡稳定性分析.

水平条分法；边坡；稳定性；人工蜂群算法

0 引 言

边坡稳定分析是土力学的经典课题.对于边坡稳定性分析，国内外学者提出了多种不同的分析方法，其中，极限平衡方法是工程上应用最广泛的分析方法[1-3].目前，极限平衡法多采用竖向条分法，我国很多规范也普遍推荐和采用[4].竖向条分法有其优越性，但也存在不足.比如，对于边坡构成为成层岩土体时，由于竖向条分体内部受岩土体性质变化影响较大，如容重不一，土体竖向抗剪强度指标变化等，给计算带来极大的不便[5].1992年，Lo等[6]首次提出了极限平衡水平条分法.1997年，Ling等[7]以极限分析理论为基础，对加筋土挡墙的稳定性进行了分析.其后，Shahgholi[8]和Nouri等[9]对该方法进行了发展和改进，水平条分的思路被引入到加筋结构的分析中，2003年，陈昌富等[5，11]根据成层岩土体的特点，采用水平条分法分析边坡稳定性，取得了较好的效果，2011年，沈振中等[10]将水平条分法应用到土石坝抗震稳定性分析.在此基础上，本研究以极限平衡原理为基础，推导出水平条分法计算公式，同时将人工蜂群算法应用于水平条分边坡最危险滑动面的搜索，把水平条分法在边坡稳定性分析中的应用做进一步的拓展.

1 水平条分法

目前，竖向条分法常用的有瑞典圆弧法、Bishop法、Janbu法与 Morgenstern-Price法等[12-13].而水平条分法与竖向条分法一样，将滑动土体分成若干条块，然后根据工程力学概念和原理，建立力平衡方程与力矩平衡方程，从而求解滑动面的安全系数，其不同之处在于水平条分法将滑动体划分成若干水平条块.

1.1 基本假定及条块划分

在推导水平条分法公式时做如下假定:

①滑动面为圆弧形；

②每一条块上的竖向应力为其超载；

③滑裂面不穿过坡角；

④土条底部Ni和Ti合力作用点位置为土条底部的中点；

⑤相邻条块之间的条间力不受条块划分方向的影响.

水平条分法的条块划分如图1(a)所示.

图1(a)中，A点为坐标原点，取单位长度，按平面问题计算.设可能滑动面是一圆弧AC，圆心为O，半径为R.将滑动体分为n个水平向条块，且每一条块只包含一种岩土体.在n个土条中取任一水平向条块i，其受力如图1(b)所示.

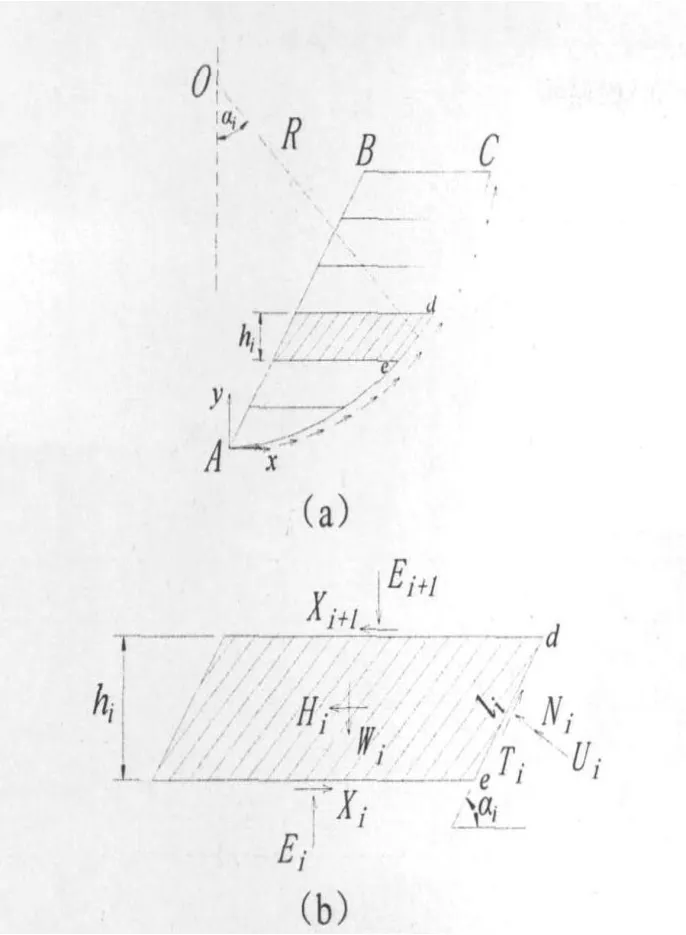
图1 水平条分法条块受力分析图

图1(b)中，Wi为土条自重，Hi为作用在土条上的水平向地震荷载，Ni和Ti分别为滑动面de上的法向应力和切向应力，它们的大小均未知，Ui为滑动面de上孔隙水压力，Ei和Ei+1分别为第i-1和i+1条块作用在第i条块的法向应力(相当于上覆土层的重量)，Xi和Xi+1分别为第i-1和i+1条块作用在第i条块的水平剪切应力；li为土条底部(滑动面de)长度，αi为土条的水平倾角，hi为土条高度.

1.2 力平衡方程

在图1(b)中，根据极限平衡原理，每个条块上水平方向和竖直方向上的作用力平衡，即，

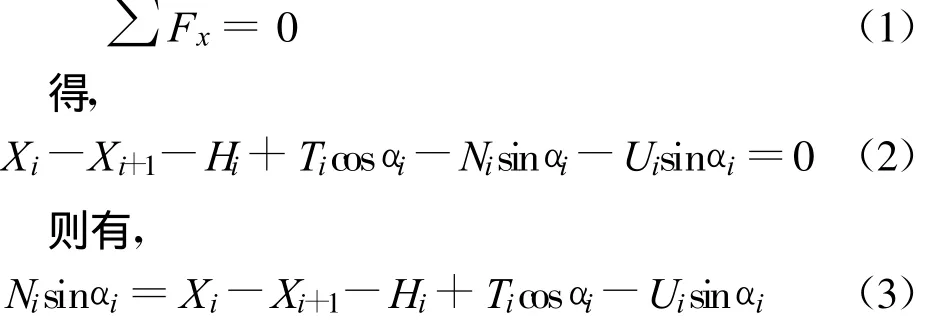
水平向地震荷载Hi的计算式为，

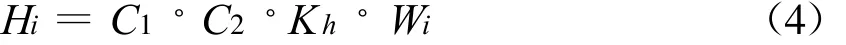
式中，C1为重要性修正系数，按规范表1.0.4采用[1]；C2为综合影响系数，取C2=0.25；Kh为水平地震系数，基本烈度为7，8，9度时，分别取0.1，0.2，0.4[1].

假定相邻条块间的条间力不受条块划分方向的影响，则仍可采用Morgenstern和Price提出的形式，即假定条块间水平剪切应力和法向应力之间存在函数关系[14]，

式中，λ为调整Xi和Ei比例关系的待定参数，λ∈(0，1)；fi(y)为沿竖直方向坐标的函数.

假定fi(y)=1，则式(5)可简化[6]为，

若边坡的稳定性安全系数为FS，假设滑动面上的抗剪强度τfi与滑动面上的切向力Ti平衡，即，

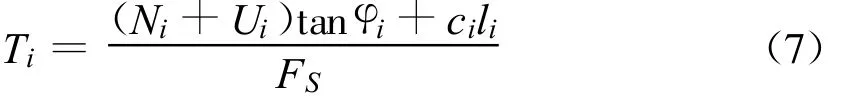
1.3 力矩平衡方程

在图1(a)中，对于圆弧形滑面，条块对圆心O取矩，力矩也要平衡，即，

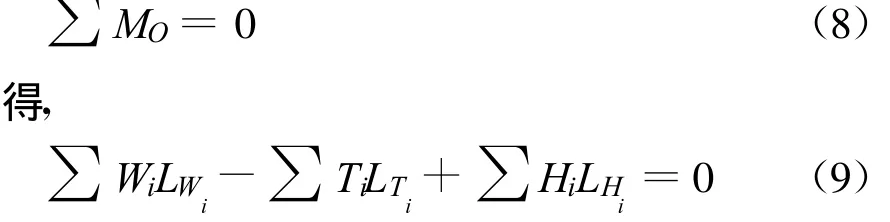
式中，LWi为条块i的重力Wi对圆心O的力臂，LTi为条块i的总切向力Ti对圆心O的力臂，LHi为条块i的水平向地震荷载Hi对圆心O的力臂.

1.4 公式推导

将式(7)代入式(3)，得，

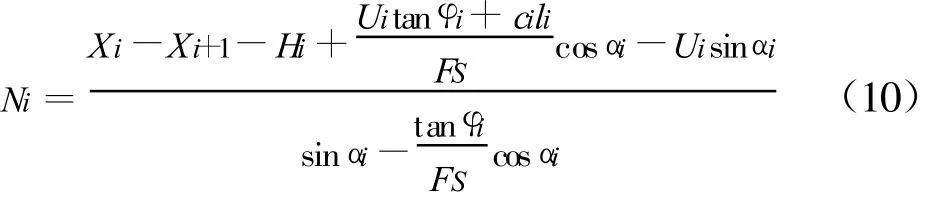
将式(7)代入式(9)，得，

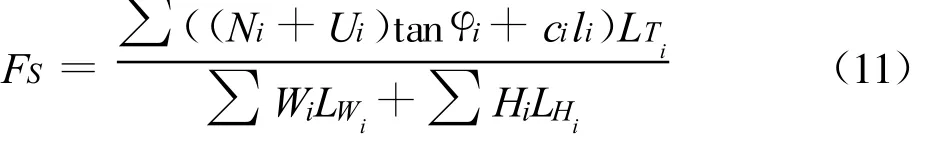
由式(10)及(11)知，Ni的计算式中包含FS值，FS的计算式中包含Ni，因此可采用迭代法求解.

2 最危险滑动面搜索的人工蜂群算法

边坡稳定性分析的关键在于确定最危险滑动面以及与之相对应的边坡稳定性安全系数FS.对于采用竖向条分法的边坡稳定分析，搜索边坡最危险滑动面和确定边坡安全系数的方法很多，这些方法在工程中应用广泛，并形成了一套完整的经验指标体系和工程指标体系.但是，由于水平条分法起步较慢，目前对于用水平条分法搜索其危险滑动面的方法相对较少.本研究采用人工蜂群算法对边坡最危险滑动面进行搜索.

人工蜂群算法(Artificial Bee Colony，ABC)是由Karaboga等[15]提出的一种新颖的模仿蜂群采蜜行为的群集智能优化算法.该方法通过各人工蜂个体的局部寻优行为，最终在群体中使全局最优值突现出来，具有全局优化能力强和自适应收敛等优点，该算法主要包含以下几个主要步骤[16-18]:

1)随机产生一个初始种群xij，i=1，2，…，SN，j=1，2，…，m，其中SN为蜜源数，m为待优化变量的维数；

2)蜜蜂对所有蜜源及其适应度进行搜索、评估；

3)雇佣蜂对xij进行一次领域搜索，寻找适应度较好的蜜源vij，根据公式，

977 Effect of informationized time tracking management mode on treatment speed of acute ischemic stroke

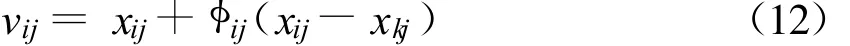
式中 ，xk是随机选择的，但xk≠xi；φij为[-1，1]中的随机数，然后在vi和xi之间运用贪婪选择原则，选择适应度较好的作为蜜源，即若vi优于xi，则用vi替换xi；

4)计算蜜源xi的概率Pi，

式中，fiti为第i个解的适应度，按下式计算，

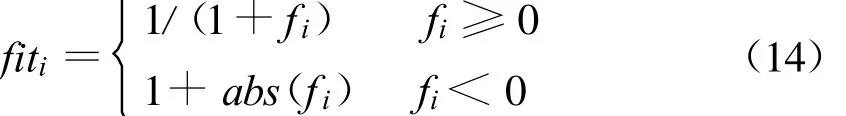
式中，fi为目标函数值.

5)观察蜂依据概率Pi，在vi和xi之间仍然采用贪婪选择原则，将xi和vi中适应度较好的作为新蜜源xi；

6)假如蜜源xi经过限定的循环次数limit不能被改进，则放弃解xi，同时相应的雇佣蜂成为侦察蜂，侦察蜂发现新蜜源x′i，并替换xi，

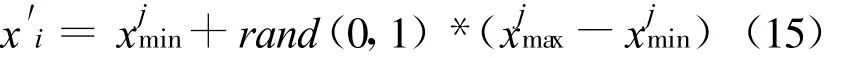
从式(12)可知，随着xkj和xij逐渐接近，对变量xkj的扰动也越来越小.因此，随着变量xij逼近最优解，步长会自适应地缩减，这就使得人工蜂群算法具有自适应收敛特性.

3 算例分析

有一水平向成层岩土体结构边坡，其剖面形态及几何参数如图2所示，构成边坡各层岩土体物理力学参数见表1.

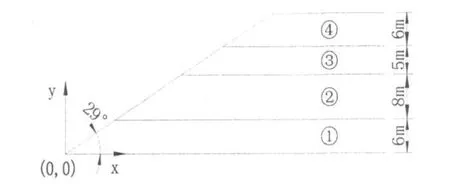
图2 坡面形态和几何参数

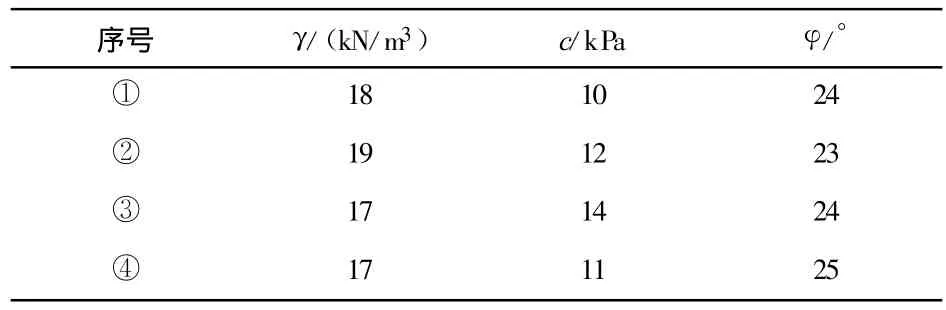
表1 各土层物理力学参数表

为分析基于人工蜂群算法的水平条分法的可靠性，本研究将其与国内外常用的边坡稳定性分析方法进行了对比分析，即采用瑞典条分法、Bishop法、Janbu法与Morgenstern-Price法及本研究方法对边坡最危险滑动面进行搜索，并计算相应的边坡稳定性安全系数FS.其中，前4种方法的最危险滑动面采用GeoStudio软件SLOPE模块进行搜索，对于本研究提出的水平条分法，采用人工蜂群算法搜索最危险滑动面，计算过程将土条划分为50条，λ取0.16.最危险滑动面及其安全系数计算结果如表2所示.

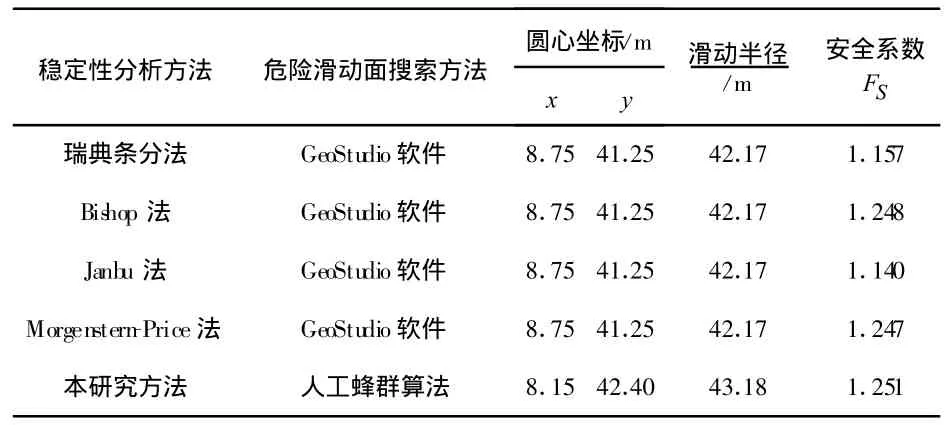
表2 稳定性分析方法计算结果

从表2结果可知，本研究方法与其他几种稳定性分析方法计算结果接近，说明本研究提出的基于人工蜂群算法的水平条分法是可靠的.

4 结 语

本研究采用基于人工蜂群算法的水平条分法进行边坡稳定性分析，并得出如下结论:

1)以极限平衡法的基本原理为基础，推导出了地震荷载作用下，存在地下水条件时，满足力平衡方程和力矩平衡方程的水平条分法计算公式.

2)首次将基于人工蜂群算法的水平条分法应用到成层状岩土体边坡稳定性分析中，该方法计算结果与瑞典条分法、Bishop法、Janbu法、Morgenstern-Price法计算结果相近，表明该方法计算结果是可靠的.

3)边坡最危险滑动面搜索是一个较复杂的数学规划问题.本研究选用全局优化及自适应能力强的人工蜂群算法进行边坡最危险滑动面的搜索，克服了传统算法易陷于局部最优解的缺点.

:

[1]中交第二公路勘察设计研究院.JTG D30-2004公路路基设计规范[S].北京:人民交通出版社，2004.

[2]交通部公路规划设计院.JTJ 044-89公路工程抗震设计规范[S].北京:人民交通出版社，1989.

[3]中国水利水电科学研究院.DL 5073-2000水工建筑物抗震设计规范[M].北京:中国电力出版社，2000.

[4]中华人民共和国铁道部.GB 50111-2006铁路工程抗震设计规范[S].北京:中国计划出版社，2006.

[5]陈昌富，杨宇，龚晓南.基于遗传算法地震荷载作用下边坡稳定性分析水平条分法[J].岩石力学与工程学报，2003，22(11):1919-1923.

[6]Lo S C R，Xu D W.A strain-based designmethod for the collapse limit state of reinforced soil walls or slopes[J].Canadian Geotechnical Journal，1992 ，19(5):832-842.

[7]Ling H I，Leshchinsky D，Perry E B.Seismic design and performance of geosynthetic-reinforced soil structures[J].Geotechnique，1997，47(5):933-973.

[8]Shahgholi M ，Fakher A ，JonesC J F P.Horizontal slice method of analysis[J].Geotechnique，2001 ，51(10):881-885.

[9]Nouri H ，Fakher A ，Jones C J F P.Development of horizontal slice method for seismic stability analysis of reinforced slopes and walls[J].Geotextiles and Geomembranes，2006 ，24(2):175-187.

[10]沈振中，崔娟，任华春.土石坝抗震稳定性分析的极限平衡水平条分法[J].南水北调与水利科学，2011，9(6):146-166.

[11]陈昌富，杨宇.边坡稳定性分析水平条分法及其进化计算[J].湖南大学学报(自然科学版)，2004，31(3):72-74.

[12]钱家欢，殷宗泽.土工原理与计算[M].北京:水利电力出版社，1994.

[13]陈祖煜.土质边坡稳定性分析原理、方法、程序[M].北京:中国水利水电出版社，2003.

[14]Morgenstern N R，Price V E.The analysis of the stability of general slip surface[J].Geotechnique，1965，15(1):79-93.

[15]Karaboga D，Basturk B.On the performance of artificial bee colony(ABC)algorithm[J].Applied Soft Computing，2008，8(1):687-697.

[16]康飞，李俊杰，马震岳.基于人工蜂群算法的边坡最危险滑动面搜索[J].防灾减灾工程学报，2011，31(2):166-172.

[17]Chen Guangzhou，Wang Jiaquan，Li Chuanjun.Identification of parameters in kinetic models usingartificial bee colony algorithm[J].Advances in Information Technology and Industry Applications，2012(136):323-329.

[18]岳云力.基于改进人工蜂群算法的机组组合优化方法[D].杭州 :浙江大学 ，2012.

Study on Slope Stability Evaluation of Horizontal Slice Method Based on Artificial Bee Colony Algorithm

QIN Liang1，PEI Xiangjun1，CHEN Xiyang2

(1.College of Environment and Civil Engineering，Chengdu University of Technology，Chengdu 610059，China；2.China Machinery TIDI Geotechnical Engineering Co.，Ltd.，Wuhan 430030，China)

According to the basic principle of limit equilibrium method，the formula of horizontal slice method is derived for the stability analysis of layered strata slopes under the action of earthquake.We introduce artificial bee colony algorithm into searching for the most dangerous sliding surface in slope for horizontal slice method and develop the limit equilibrium horizontal slice method of slope stability based on artificial bee colony algorithm.The example shows that this method is able to find out the global optimal solution rapidly and has reliable computation results，which is suitable for the stability analysis of layered strata slopes.

horizontal slice method ；slope ；stability ；artificial bee colony algorithm

TU435

A

1004-5422(2013)01-0082-04

2012-12-26.

地质灾害防治与地质环境保护国家重点实验室自由探索基金(SKLGP2009Z009)资助项目.

覃 亮(1988—)，男，硕士研究生，从事地质灾害评价与预测研究.