非对称共面波导弯曲结构模式转换的研究
陈宏巍 房少军
(大连海事大学,信息科学技术学院,辽宁 大连 116026)
引 言
共面波导(Coplanar Waveguide,CPW)由于具有易于串并联、低损耗、低色散、集成度高等优点被广泛应用于微波集成电路之中[1-2].在设计复杂电路时,共面波导弯曲结构、T型结等这些不连续电路是不可避免的[3].然而,这些不连续部分常会在传输偶模信号的同时激励起奇模信号,造成电路的传输损耗较高.
归纳以往的研究,抑制奇模信号在CPW弯曲结构中传输的方法主要有三种:一是在CPW的地平面上跨接空气桥,对奇模信号形成短路,而对偶模信号影响较小[4];二是应用上或下屏蔽平面,由于屏蔽平面与地平面的电位相同,使得奇模信号在这种情况下很难传输[5];三是增加补偿电路结构,例如:在共面波导较长缝隙的介质上周期地打孔或将较短的缝隙设计成齿状结构[6-8],由于提高或者降低了一侧缝隙中信号的传输速率,使得共面波导两侧缝隙的信号相位始终相同,也能对奇模信号起到抑制作用.然而所有这些方法都具有一定的局限性.主要体现在两方面:一是由于改变了传输线的结构,增加了设计和制作难度;二是传输线结构的改变势必改变传输线的特性阻抗,对于原先设计为直线的CPW,中间引入一段特性阻抗不同的传输线,必然会使整体的阻抗匹配恶化.需要特别指出的是,文献[8]提出采用共面波导-非对称共面波导(CPW-ACPW)周期结构提高CPW弯曲结构的性能,但是其原理仍属于第三种方法,且没有对非对称共面波导(Asymmetric Coplanar Waveguide,ACPW)弯曲结构进行深入分析.
在过去的几十年中,许多学者使用不同的方法分析了CPW弯曲结构.其中,Omar等人应用矩量法详细研究了空气桥的长度、宽度和高度对CPW弯曲结构的影响[9];MingDong WU应用混合势积分方程分析了无空气桥的CPW弯曲结构[10],详细研究了CPW弯曲结构的模式转换特性,指出在某些特定频段CPW弯曲结构中模式转换是不可避免的.然而,上述分析方法均为频带较窄的频域算法,近年发展起来的时域多分辨率分析(Multi-Resolution Time Domain,MRTD)方法可以在较宽的频带内保持良好的精度.并且该方法与当前流行的时域有限差分法(Finite Difference Time Domain,FDTD)相比,除了有较低的数值色散外,其最突出的特点是每个波长采2个点可达到FDTD每个波长10个点的精度,其空间网格个数只有三维FDTD的1/125.由此可见,MRTD算法对计算机资源的节省是相当可观的[11].
Tripathi于1974年将传输在非对称平行耦合双线中的信号分解为c模和π模信号[12],并证明了偶模和奇模是其在平行耦合双线对称时的特例.而事实上CPW和ACPW分别属于对称的和非对称的平行耦合双线.本文利用时域多分辨率分析(MRTD)算法和从Y参数提取了c模、π模特性阻抗的方法,对ACPW弯曲结构模式转换性能进行了分析.最后,提出了一种吸收π模的实验装置,并将其应用于CPW和ACPW弯曲结构的测试.
1 理论分析
1.1 ACPW中的c模和π模
图1为ACPW弯曲结构端口电压、电流的定义以及c模信号示意图.图中和为c模信号位于槽1和槽2的正向电压分布,和为c模信号位于槽1和槽2的反向电压分布.如果用、I、和表示c模信号位于槽1和槽2的正向、反向电流分布,则可以定义槽i的c模特性阻抗为

如果将公式(1)中的下标c换成π,即为π模特性阻抗定义.并且c模电压与π模电流之间,以及π模电压与c模电流之间有如下关系[13-14]为
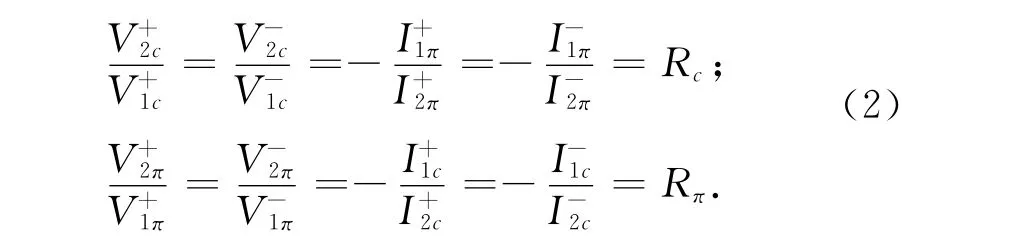
式中Rc、Rπ为两个槽的模式电压比,如果Rc=1、Rπ=-1,则c模退化成偶模,π模退化成奇模.
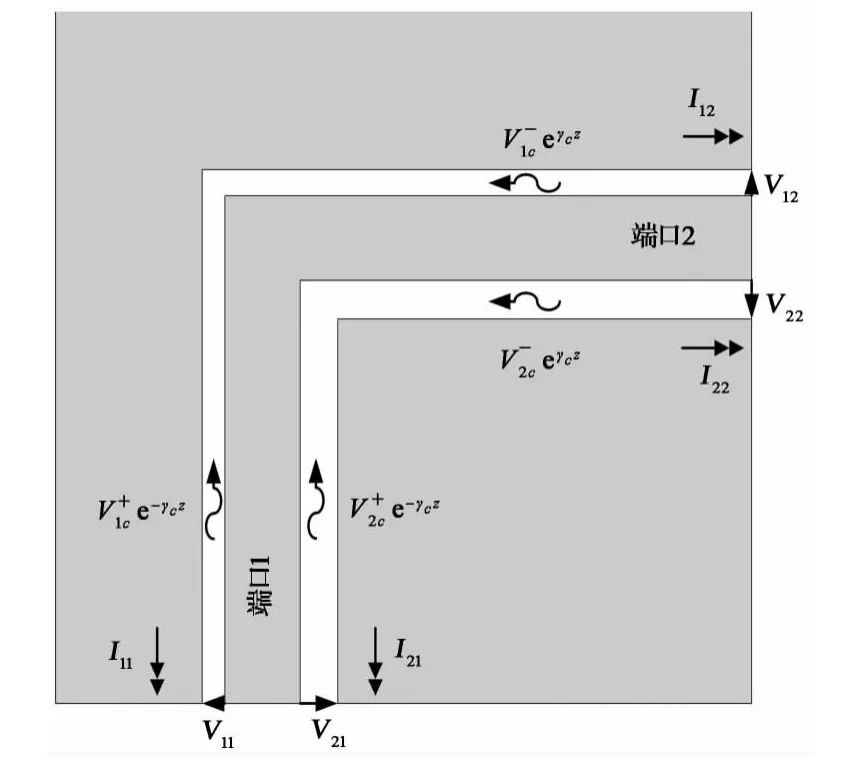
图1 端口电压、电流和c模信号示意图
1.2 散射矩阵
令ACPW弯曲结构上端口1处的位置坐标z=0,则端口1上的电压和电流满足下列方程为
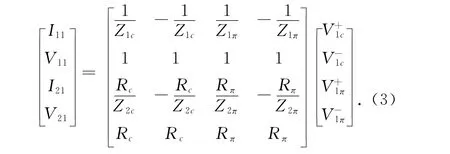
式中,V11、I11、V21和I21分别为图1所示端口1上两个槽的电压和电流.解方程(3)可以计算出瞬时c模和π 模的正、反向电压和,进一步对这些信号做傅里叶变换,得到频域的正、反向电压和,接下来利用下列公式:

可以得到端口1归一化c模、π模的入射波和反射波ac1、bc1、aπ1和bπ1.在端口2上做同样的处理,可以得到端口2上归一化c模、π模的入射波和反射波ac2、bc2、aπ2和bπ2.最终,入射波、反射波和散射矩阵的关系可以写为
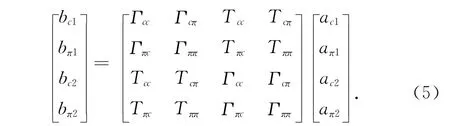
式中 Tij(i=c,π;j=c,π)为传输系数,Γij(i=c,π;j=c,π)为反射系数.在应用 MRTD算法时,通常需要对弯曲结构计算模型激励4次,才能计算出散射矩阵的16个未知元素.但是ACPW弯曲结构具有互易性和对称性,因此只要对计算模型激励2次即可.
2 数值计算与测试
2.1 数值计算结果与讨论
在应用MRTD方法(选用Daubechies尺度函数为基函数)计算时,导体设为理想导体和零厚度,并使用7层的PML吸收层.其中所使用的网格尺寸如表1所示,p阶消失矩的Daubechies尺度函数的关联系数a(i)如表2所示[15].计算所使用的物理参数包括:介电常数10.2,介质厚度0.635mm,导体厚度0.035mm,中心导体宽度1.925mm,ACPW两个槽宽分别为0.385mm和1.350mm.
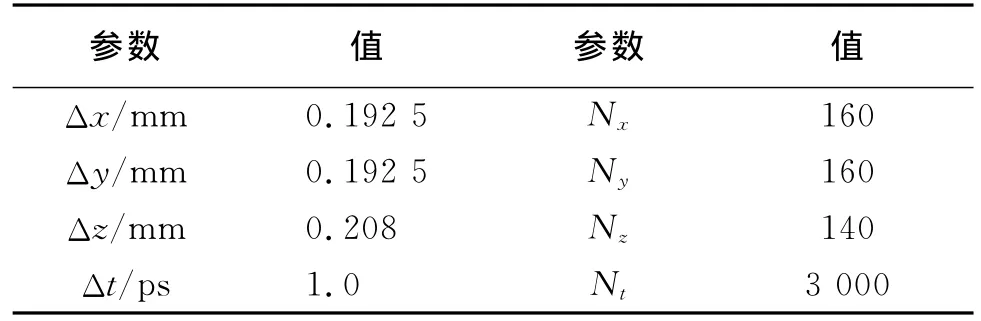
表1 MRTD计算参数
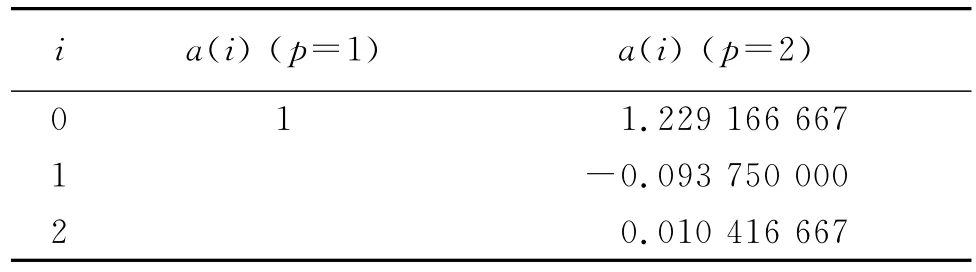
表2 p阶消失矩的Daubechies尺度函数的关联系数
在MRTD计算结果的基础上,从Y参数出发提取了相位常数、特性阻抗和模式电压比[16],并与Ansys公司高频结构仿真器(High Frequency Structure Simulator,HFSS)的仿真结果进行对比.图2为这两种方式获得的相位常数.图中高频部分一致性较好,低频部分HFSS的仿真结果偏低,这是因为,在HFSS仿真的模型中必须以理想导体作为端口边界,抑制了π模信号的传输.表3为两种方式计算的特性阻抗及模式电压比.其中两种方式获得的模式电压比及c模特性阻抗比较接近,而π模特性阻抗偏差较大,但是这并不影响对非对称共面波导弯曲结构的分析.

图2 归一化的c模和π模传播常数

表3 特性阻抗和模式电压比
利用公式(5)可以计算出传输系数随频率变化的曲线,如图3所示.
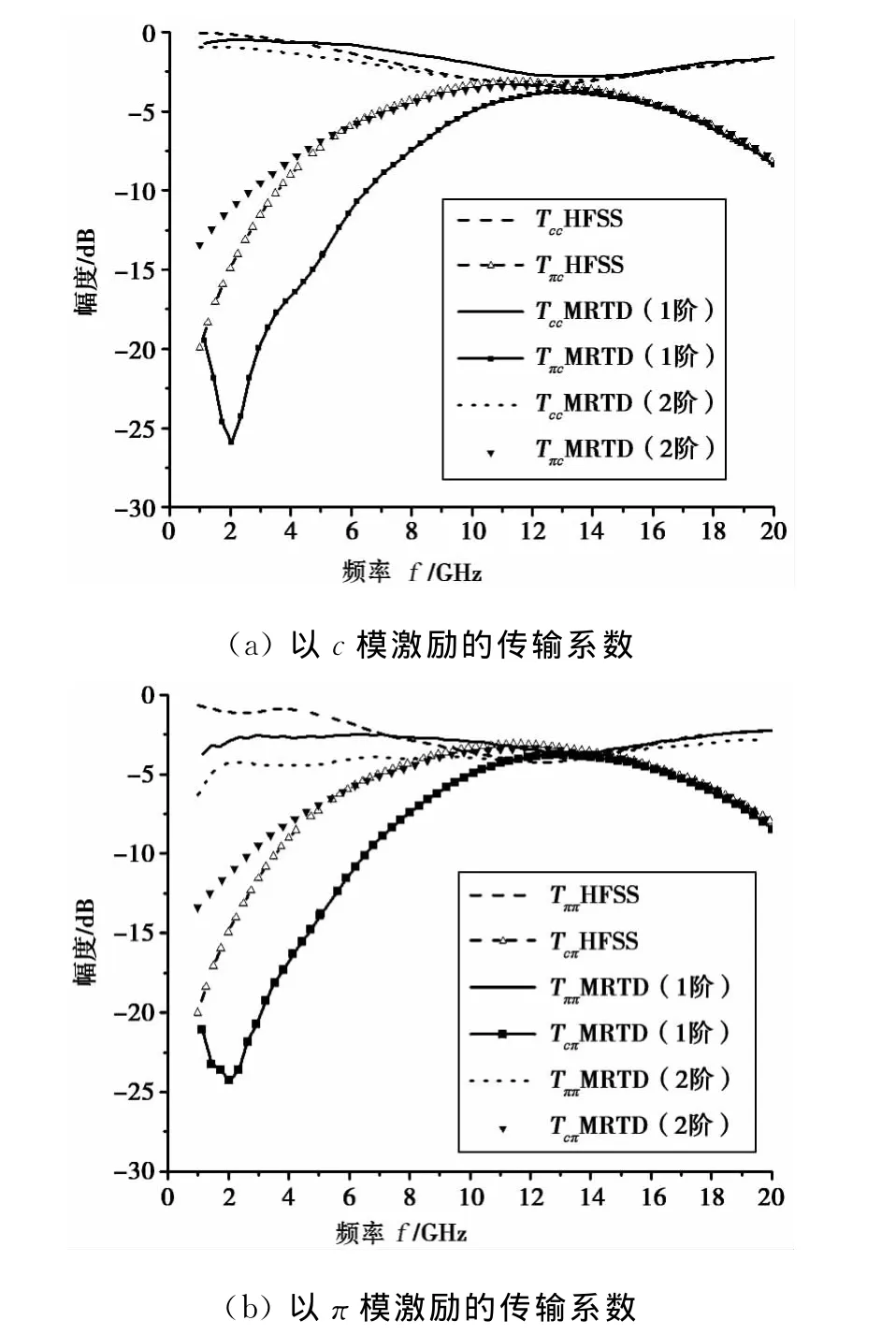
图3 ACPW弯曲结构的传输系数
在13GHz附近传输系数Tπc、Tcπ达到了最大值约-3.8dB,同时传输系数Tcc、Tππ减小为最小值约-3dB.这说明某一种模式信号在端口1激励,到达端口2时,低于41.7%的能量转换为另一种模式的信号.相比之下,偶模信号经过CPW弯曲结构以后,在特定的频段内完全转换为奇模信号[5].从HFSS与MRTD算法仿真对比来看,2阶消失矩的MRTD方法计算结果与HFSS仿真的结果较为接近.
2.2 实验结果分析
矢量网络分析仪测试端口为同轴形式的接口,然而这种接口只能传输TEM模,直接测试ACPW弯曲结构的结果只能是c模和π模的混合信号.因此,不能直接使用矢量网络分析仪测试ACPW弯曲结构散射矩阵的各个元素.如果设定ACPW中心导体为0电位,那么对c模而言ACPW导体的电位为“-0-”;对π模而言电位为“+0-”,如图4(a)所示.如果在两个地平面之间跨接一个电阻,起到吸收π模信号的作用;同时,将中心导体变细使阻抗连续,确保c模信号的传输,如图4(b)所示.这样既可以测试到c模信号,又降低了π模信号的干扰.
使用Taconic CER-10板材加工制作了有吸收电阻和无吸收电阻的ACPW弯曲结构以及有吸收电阻的CPW弯曲结构,实物照片如图5所示.三种弯曲结构的物理参数与仿真计算的物理参数一致,其中吸收电阻为80Ω,CPW的槽宽为0.7mm.
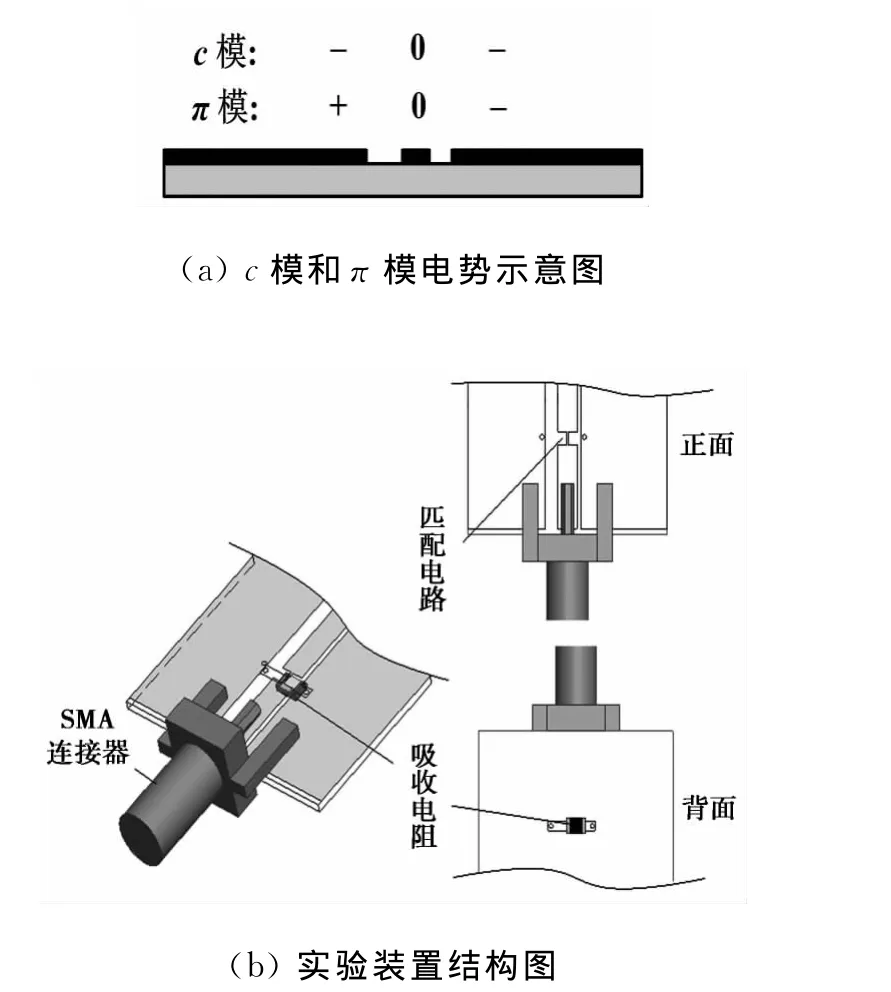
图4 吸收π模的实验装置

图5 CPW和ACPW弯曲结构的实物照片
图6为三种弯曲结构的S参数测试曲线对比.由图可知,ACPW弯曲结构加入吸收电阻后,|S21|曲线变得很平坦,说明电阻起到了对π模的抑制作用.从图中还可以看到,ACPW弯曲结构的|S21|没有在整个频段,而是仅在较高频段大于CPW弯曲结构的|S21|.这是因为在频率较低时,电阻吸收了一部分ACPW弯曲结构c模信号能量,而对CPW弯曲结构的偶模信号影响很小;在较高频段时,虽然仍有一部分c模信号能量被电阻吸收掉,但是ACPW弯曲结构c模信号转换成π模信号的能量很小.所以,表现出在较低频段ACPW弯曲结构|S21|测试结果偏低的现象.结合理论分析,可以确定:与CPW弯曲结构相比,ACPW弯曲结构模式间能量转换更小.
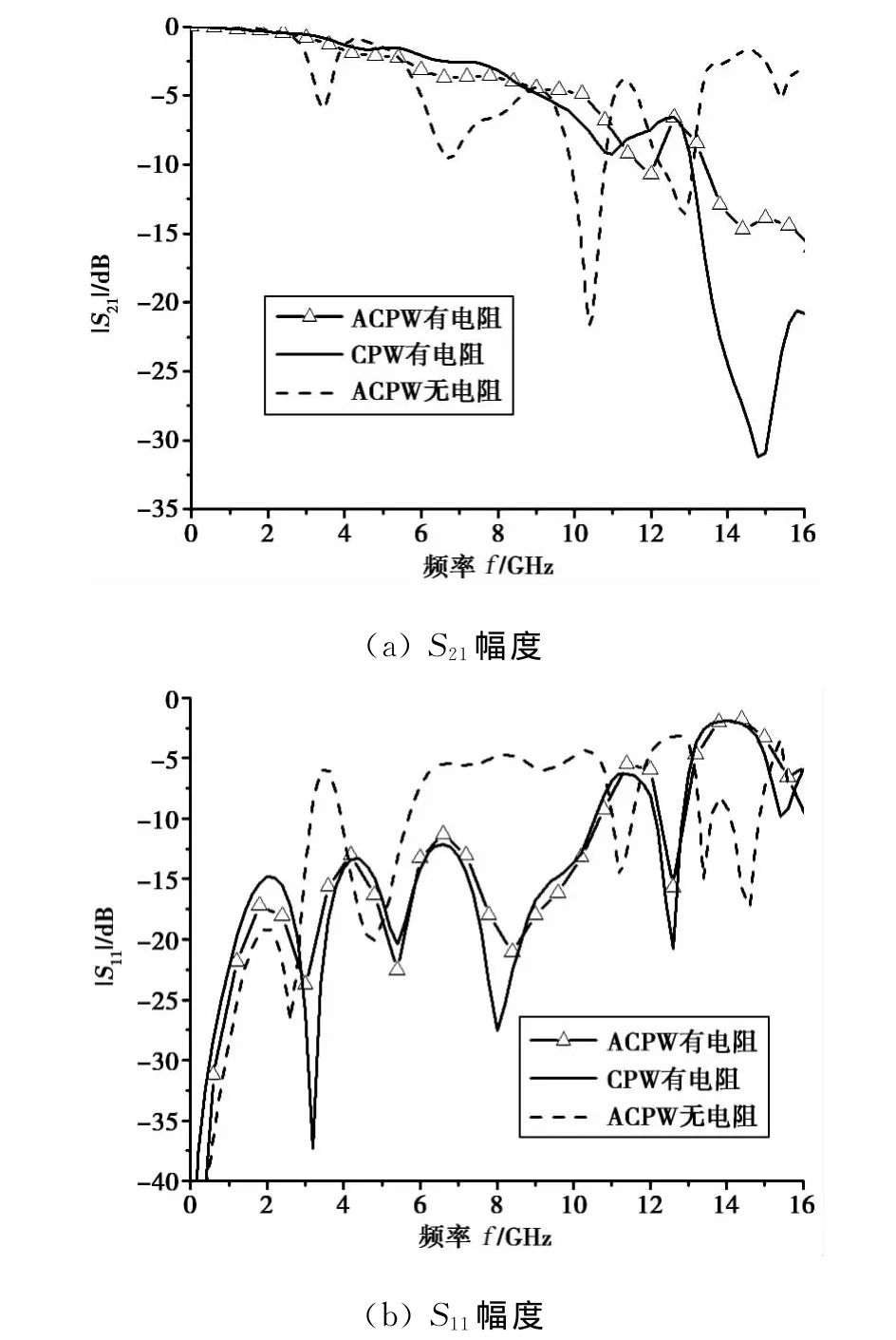
图6 三种弯曲结构的测试对比
3 结 论
文中提出了一种基于MRTD算法的c模、π模分解技术.通过结合MRTD算法和从Y参数提取特性阻抗的方法,推导出了4×4阶的散射矩阵计算公式;在此基础上研究了ACPW弯曲结构的模式间能量转换现象.对比CPW弯曲结构,发现ACPW弯曲结构的模式间能量转换较小.此外,提出了一种吸收π模的实验装置,对理论分析的结论进行了验证.研究结果表明ACPW弯曲结构性能好于CPW弯曲结构,实际工程中应当用ACPW弯曲结构代替CPW弯曲结构设计微波电路.
[1]WEN C P.Coplanar waveguide:A surface strip transmission line suitable for nonreciprocal gyromagnetic device applications[J].IEEE Trans Microwave Theory and Techniques,1969,17(12):1087-1090.
[2]JACKSON R W.Considerations in the use of coplanar waveguide for millimeter-wave integrated circuits[J].IEEE Trans Microwave Theory and Techniques,1986,34(12):1450-1456.
[3]HIROTA T,TARUSAWA Y,OGAWA H.Uniplanar MMIC hybrids-aproposed new MMIC structure[J].IEEE Trans Microwave Theory and Techniques,1987,35(6):576-581.
[4]RIAZIAT M,ZUBECK I,BANDY S,et al.Coplanar waveguides used in 2-18GHz distributed amplifier[C]//IEEE MTT-S International Microwave Symposium Digest.Baltimore,June 2-4,1986:337-338.
[5]OMAR A A,CHOW Y L.Coplanar waveguide with top and bottom shields in place of air-bridges[J].IEEE Trans Microwave Theory and Techniques,1993,41(9):1559-1563.
[6]张 卉,王均宏.奇模抑制孔缝阵列速度补偿型弯曲共面波导[J].电波科学学报,2009,24(2):228-232.ZHANG Hui,WANG Jun Hong,Velocity compensated CPW bend for odd-mode suppression by hole array[J].Chinese Journal of Radio Science,2009,24(2):228-232.(in Chinese)
[7]KIM H,FRANKLIN-DRAYTON R.Wire-bond free techinique for right-angle coplanar waveguide bend structures[J].IEEE Trans Microwave Theory and Techniques,2009,57(2):442-448.
[8]李晓明,房少军,裴 慧,等.一种非对称共面波导相位补偿弯曲结构[J].电波科学学报,2011,26(1):84-89.LI Xiaoming,FANG Shaojun,PEI Hui,et al.Novel CPW-ACPW phase compensated structure in CPW bend[J].Chinese Journal of Radio Science,2011,26(1):84-89.(in Chinese)
[9]OMAR A A,CHOW Y L,ROY L,STUBBS M G.Effects of air-bridges and mitering on coplanar waveguide 90°bends:theory and experiment[C]//IEEE MTT-S Digest.Atlanta,June 14-18,1993,823-826.
[10]WU Mingdong,DENG Shengming,WU R B,et al.Full-wave characterization of the mode conversion in a coplanar waveguide right-angled bend[J].IEEE Trans Microwave Theory and Techniques,1995,43(11):2532-2538.
[11]李炎红,杨 峰,聂在平,等.基于MRTD的微带天线的辐射分析[J].电波科学学报,2010,25(4):674-678.LI Yanhong,YANG Feng,NIE Zaiping,et al.Microstrip antenna radiation based on MRTD method[J].Chinese Journal of Radio Science,2010,25(4):674-678.(in Chinese)
[12]TRIPATHI V K.Asymmetric coupled transmission lines in an inhomogeneous medium[J].IEEE Trans Microwave Theory and Techniques,1975,23(9):734-739.
[13]MONGIA R K,BAHL I J,BHARTIA P,et al.U-niformly Coupled Asymmetrical Lines[M].London:Artechhouse,1998.
[14]KRAGE M K,HADDAD G I.Characteristics of coupled microstrip transmission lines-I:Coupledmode formulation of inhomogeneous lines[J].IEEE Trans Microwave Theory and Techniques,1970,18(4):217-228.
[15]高强业.时域多分辨方法研究及其在电磁散射中的应用[D].南京:南京航空航天大学,2011.GAO Qiangye.A Study on the Multiresolution Timedomain Method and Its Applications to Electromagnetic Scattering Problems[D].Nanjing:Nanjing University of Aeronautics and Astronautics.
[16]TRIPATHI V K,LEE H.Spectral-domain computation of characteristic impedances and multiport parameters of multiple coupled microstrip lines[J].IEEE Trans Microwave Theory and Techniques,1989,37(1):215-220.

